沪科版九年级上册 数学 21.4 二次函数的应用课件(46张PPT)
文档属性
| 名称 | 沪科版九年级上册 数学 21.4 二次函数的应用课件(46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 676.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 20:13:43 | ||
图片预览










文档简介
21.4 二次函数的应用
复习
二次函数解析式有哪几种表达式?
一般式:y=ax2+bx+c (a≠0)
顶点式:y=a(x-h)2+k (a≠0)
交点式:y=a(x-X1)(X-X2) (a≠0)
1 已知图象上三点或三对的对应值,通常选择一般式
2 已知图象的顶点坐标(对称轴和最值)通常选择顶点式
3 已知图象与x轴的两个交点的横坐标x1、x2,通常选择交点式
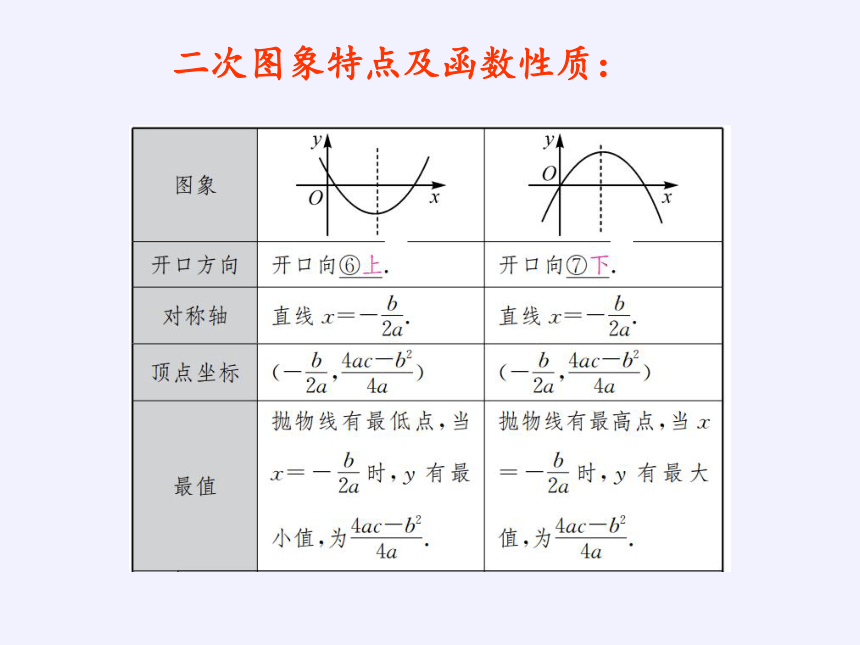
二次图象特点及函数性质:
例1 已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
(一) 根据函数图象特点及性质求函数解析式
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x
解:
根据题意得顶点为(-1,4)
由条件得与x轴交点坐标(2,0);(-4,0)
例2(如图所示)已知当x=-1时,抛物线最高点的
纵坐标为4,且与x轴两交点之间的距离为6,求此函
数解析式
y
o
x
设二次函数解析式:y=a(x-2)(X+4)
故所求的抛物线解析式为 y= (x+1)2+4
把(-1,4)代入y=a(x-2)(X+4) 得 a=
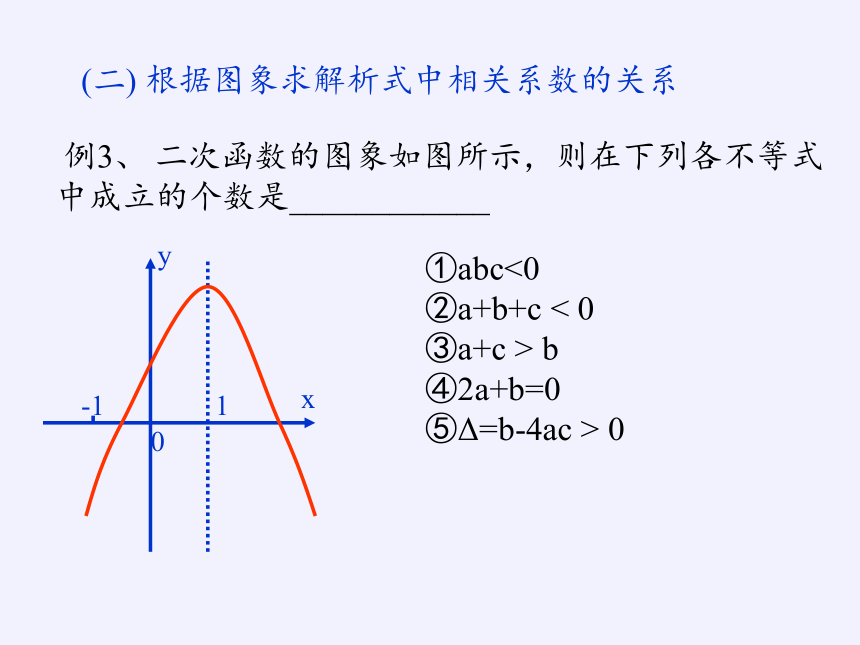
例3、 二次函数的图象如图所示,则在下列各不等式
中成立的个数是____________
1
-1
0
x
y
①abc<0
②a+b+c < 0
③a+c > b
④2a+b=0
⑤Δ=b-4ac > 0
(二) 根据图象求解析式中相关系数的关系
(1)a确定抛物线的开口方向:
a>0
a<0
(2)c确定抛物线与y轴的交点位置:
c>0
c=0
c<0
(3)a、b确定对称轴 的位置:
ab>0
ab=0
ab<0
(4)Δ确定抛物线与x轴的交点个数:
Δ>0
Δ=0
Δ<0
x=-
b
2a
例4、如图,在平面直角坐标系中,O为坐标原点,抛物线 y=ax2+bx+c的顶点为(-3, ),与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C. D是BO的中点,直线DC的解析式为y=kx+4.
(三) 根据图象求一系列相关问题
(1)求抛物线的解析式;
(2)求直线CD的解析式;
(3)求△ADC的面积;
(4)在抛物线上是否存在点P,使得PB=PD,求此时P点的坐标;
(5)点P是抛物线对称轴上一点,求PA+PC的值最小时,P点的坐标;
③是否存在t,使得S△CDP=S△BDP成立,若存在,求t的值,若不存在,说明理由;
④若PD将四边形BPCD的面积分成2∶3的两部分,求t的值;
(1)【思维教练】抛物线的解析式有一般式,顶点式和交点式三种形式.题中给出了抛物线的顶点坐标,故可将抛物线设为顶点式,再结合直线CD的解析式y=kx+4可得C点坐标,代入所设的抛物线即可求解.
(6)点P是抛物线上一个动点(不与点C重合),若S△BDP=S△BDC,求点P的坐标;
(7)点P是抛物线在第二象限部分图象上一点,连接PD,PC,若点P的横坐标为t.
①写出S△CDP关于t的函数关系式;
②计算S△CDP的最大值,及此时点P的坐标;
解:∵直线CD的解析式为y=kx+4,
∴与y轴交点坐标C为(0,4),
∵抛物线的顶点坐标为(-3, ),
∴抛物线解析式可设为y=a(x+3)2+ ,
将点C(0,4)代入得a(0+3)2+ =4,
解得a=- ,
∴抛物线解析式为y=- (x+3)2+ ,
即y= .
(2)【思维教练】要求直线CD的解析式,需知点C、D的坐标,结合题意,C点坐标已知,只需求得D点坐标代入解析式即可,由点D是BO的中点,结合抛物线求得B点坐标即可得D点坐标.
解:令y=- x2- x+4=0,
解得x1=-8,x2=2.
∴点A(2,0),点B(-8,0).
∵点D是OB的中点,
∴点D(-4,0),
将点D代入直线y=kx+4得-4k+4=0,
解得k=1,
∴直线CD的解析式为y=x+4.
(3)【思维教练】因为△ACD的AD边在坐标轴上,C点坐标已知,则由S△ADC= ·CO·AD求解即可.
解:∵D(-4,0),A(2,0),∴AD=6,
∵OC=4,∴S△ADC= AD·OC= ×6×4=12.
(4)【思维教练】若PB=PD,则P为BD的垂直平分线与抛物线的交点.
解:当PB=PD,则P点在BD的垂直平分线上,
∵点B(-8,0),点D(-4,0),
∴P点的横坐标为-6,且在抛物线上,
∴y= ,
∴P点的坐标为(-6,4).
(5)【思维教练】要求PA+PC值最小,则可找出点A或C,其中一点关于对称轴的对称点,与另一点连接与对称轴的交点即为所求的P点.
解:由题图知,B点即为A点关于对称轴的对称点,连接BC与对称轴的交点即为所求的点P.
设直线BC的解析式为y=kx+b.
∵点B(-8,0),点C(0,4).
∴ ,解得 ,
∴直线BC的解析式为y= x+4.
∴当x=-3时,y= .
∴P点的坐标为(-3, ).
(6)【思维教练】S△BDP=S△BDC,由三角形的面积公式为 ×底×高,结合题意知△BDP和△BDC的底同为BD,△BDC的高为OC,则只需求得抛物线上点到线段BD的距离等于OC的点即为P点.
解:∵S△BDP=S△BDC,
∴|yP|=yC,即yP=yC=4或yP=-yC=-4.
当yP=yC时,点P与点C关于抛物线对称轴对称,
当yP=-yC=-4时, ,
解得xP=-3± ,
即点P的坐标为(-3- ,-4)或(-3+ ,-4).
综上,满足题意的P点有3个,为(-6,4),
(-3- ,-4),(-3+ ,-4).
∵点C(0,4),对称轴为x=-3,
∴点P的坐标为(-6,4);
(7)①【思维教练】要求△CDP的面积,因为点P的位置不确定,故过点D作DE⊥x轴交抛物线于点E,分点P在点E的左、右两侧进行讨论.因为这两种情况下,△CDP的三条边均不在坐标轴或平行于坐标轴的直线上,故过点P作PG⊥x轴于点G,采用割或补的方法把它转化为易求出面积的图形来求解.
解:过D作DE⊥x轴交抛物线于E.
∵点D(-4,0),
∴点E(-4,6).
如解图①,当点P在BE段抛物线上,
即-8过P作PG⊥x轴于G,
∵点P的横坐标为t,∴PG= ,
∴S△PCD=S四边形PGOC-S△PGD-S△DOC
=
=
=- t2-5t.
如解图②,当点P在CE段时,-4则S△PCD=S四边形PGOC+S△PDG-S△DOC
综上,S=- t2-5t.
(7)②【思维教练】由①中可知S△CDP关于P点横坐标的函数关系式,若S△CDP的值最大,即用配方法求对应函数的最大值.
解:∵S=- t2-5t=- (t+5)2+ ,
∴当t=-5时,S有最大值,最大值为 .
(7)③【思维教练】若使S△CDP=S△BDP,由①知S△CDP关于t的函数关系式,结合题图BD在x轴上,易求BD的长度和S△BDP关于t的函数关系式,将两函数关系式联立求解即可得t的值,若无解,即不存在这样的t.
解:∵S△BDP= BD·yP= ×4×(- t2- t+4)=- t2-3t+8,
根据题意有- t2-3t+8=- t2-5t,解得t=-4.
即存在t=-4,使S△CDP=S△BDP .
(7)④【思维教练】由题图,PD将四边形CD分成了△BDP和△CDP两部分,且2S△BDP=3S△CDP或3S△BDP=2S△CDP,由①可知S△CDP关于t的函数关系式,由③可得S△BDP关于t的函数关系式,再根据两者之间的等量关系联立求解即可得t的值.
解:根据题意,(1)若2S△BDP=3S△PCD,
则 ,
解得t1=-2,t2=-16(舍),
(2)若3S△BDP=2S△PCD,
则 ,
解得t1=-6,t2=8(舍),
综上,存在这样的t且值分别为-2或-6.
探究三角形或四边形面积的最值问题:
1.可设动点的坐标为(t,at2+bt+c);
2.①求一边在坐标轴上的三角形面积时,取在坐标轴上的线段为底边,则底边上的高为动点的横坐标或纵坐标的绝对值;②求三条均不在坐标轴上的三角形或不规则的四边形面积时,常采用割或补的方法把它转化为易求出面积的图形;
3.用含有未知数的代数式表示出图形的面积;
4.用二次函数的知识来求最大值或最小值时,常采用配方法求解;
解决此类题目需要特别注意点的运动或者图形的变换引起的图形变化,看是否需要进行分类讨论.
二次函数图象的实际应用(难点)
例5 (2016合肥38中一模)音乐喷泉(图①)可以使喷水造型随音乐的节奏变化而变化,某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边20 m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一根根不同的抛物线(图②),这组抛物线的统一形式为y= .
例1题图
(1)若已知k=1,且喷出的抛物线,水线最大高度达3 m,求此时a、b的值;
(1)【思维教练】要求a、b的值,需找出a、b的关系式,由已知k=1可得y=x,由抛物线的顶点y=xt,及水线最大高度为3 m,可得出a、b的关系式,求解即可.
解:(1)∵y= 的顶点为 ,抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3 m,
∴ , ,
解得a= ,b=2,
即k=1,且喷出的抛物线水线最大高度达3 m时a、b的值分别是 、2;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线,水线最大高度是多少?
【思维教练】求水线的最大高度即求抛物线y=ax2+bx的顶点的纵坐标,由已知喷出的水恰好达到岸边,可得抛物线的对称轴,再根据y=ax2+bx 的顶点在直线y=x上求解即可.
(2)∵k=1,喷出的水恰好到岸边,出水口离岸边20 m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=10,y=x=10,
即此时喷出的抛物线,水线最大高度是10米;
(3)若k=2,且要求喷出的抛物线水不能到岸边,求a的取值范围.
【思维教练】求a的取值范围,需找出关于a的不等式,由已知喷出的抛物线水不能到岸边,可得对称轴 ,再结合k=2,抛物线y=ax2+bx的顶点在直线y=2x上可得b值代入不等式求解即可.
(3)∵y=ax2+bx的顶点 在直线y=2x上,
∴ ,解得b=4,
∵喷出的抛物线水线不能到岸边,出水口离岸边20 m,
∴ ,即 ,
解得:a>
例6 圣诞节期间,某商店销售一种圣诞帽,这种帽子每顶进价为10元.销售统计表明,该产品在圣诞节前每天的销售量t(顶)与每件的销售价x(元/顶)之间大致存在关系:t=-2x+80;该产品在圣诞节后每天的销售量p(顶)与每件的销售价x(元/顶)之间大致存在关系:p= (10<x≤20,p取整数).
(1)在圣诞节前这种帽子销售价定为多少元时其销售量为零;
(2)设每天所得的销售利润为y元,分别写出圣诞节前和圣诞节后y与x之间的函数关系式;
(3)求销售价定为多少时,销售利润最大,最大利润是多少?
(1)【思维教练】销售量为零,即t=0,把t=0代入t=-2x+80,求出x的值;
解:∵当t=-2x+80=0时,x=40,
∴在圣诞节前这种帽子销售价定为40元/顶时,其销售量为零;
(2)【思维教练】根据“销售利润=销售量×(销售单价-进货单价)”列出 y与x之间的函数关系式;
解:由题意,得:
①圣诞节前,y=t(x-10)=(-2x+80)(x-10)=-2x2+100x-800;
②圣诞节后,y= (10<x≤20);
(3)【思维教练】根据第(2)问中所求圣诞节前和圣诞节后y与x之间的函数关系式,分别求出圣诞节前与圣诞节后的最大销售利润,两者比较,即可求解.
解:在圣诞节前,y=-2x2+100x-800=-2(x-25)2+450,
∴当x=25时,y有最大值y1,且y1=450;
在圣诞节后,y=400- (10<x≤20, 为整数),
∴当x=20时,y有最大值y2,且y2=200;
∵y1>y2 ,
∴销售价定为25元/顶时,销售利润最大,最大利润是450元 .
谢 谢
复习
二次函数解析式有哪几种表达式?
一般式:y=ax2+bx+c (a≠0)
顶点式:y=a(x-h)2+k (a≠0)
交点式:y=a(x-X1)(X-X2) (a≠0)
1 已知图象上三点或三对的对应值,通常选择一般式
2 已知图象的顶点坐标(对称轴和最值)通常选择顶点式
3 已知图象与x轴的两个交点的横坐标x1、x2,通常选择交点式
二次图象特点及函数性质:
例1 已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
(一) 根据函数图象特点及性质求函数解析式
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x
解:
根据题意得顶点为(-1,4)
由条件得与x轴交点坐标(2,0);(-4,0)
例2(如图所示)已知当x=-1时,抛物线最高点的
纵坐标为4,且与x轴两交点之间的距离为6,求此函
数解析式
y
o
x
设二次函数解析式:y=a(x-2)(X+4)
故所求的抛物线解析式为 y= (x+1)2+4
把(-1,4)代入y=a(x-2)(X+4) 得 a=
例3、 二次函数的图象如图所示,则在下列各不等式
中成立的个数是____________
1
-1
0
x
y
①abc<0
②a+b+c < 0
③a+c > b
④2a+b=0
⑤Δ=b-4ac > 0
(二) 根据图象求解析式中相关系数的关系
(1)a确定抛物线的开口方向:
a>0
a<0
(2)c确定抛物线与y轴的交点位置:
c>0
c=0
c<0
(3)a、b确定对称轴 的位置:
ab>0
ab=0
ab<0
(4)Δ确定抛物线与x轴的交点个数:
Δ>0
Δ=0
Δ<0
x=-
b
2a
例4、如图,在平面直角坐标系中,O为坐标原点,抛物线 y=ax2+bx+c的顶点为(-3, ),与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C. D是BO的中点,直线DC的解析式为y=kx+4.
(三) 根据图象求一系列相关问题
(1)求抛物线的解析式;
(2)求直线CD的解析式;
(3)求△ADC的面积;
(4)在抛物线上是否存在点P,使得PB=PD,求此时P点的坐标;
(5)点P是抛物线对称轴上一点,求PA+PC的值最小时,P点的坐标;
③是否存在t,使得S△CDP=S△BDP成立,若存在,求t的值,若不存在,说明理由;
④若PD将四边形BPCD的面积分成2∶3的两部分,求t的值;
(1)【思维教练】抛物线的解析式有一般式,顶点式和交点式三种形式.题中给出了抛物线的顶点坐标,故可将抛物线设为顶点式,再结合直线CD的解析式y=kx+4可得C点坐标,代入所设的抛物线即可求解.
(6)点P是抛物线上一个动点(不与点C重合),若S△BDP=S△BDC,求点P的坐标;
(7)点P是抛物线在第二象限部分图象上一点,连接PD,PC,若点P的横坐标为t.
①写出S△CDP关于t的函数关系式;
②计算S△CDP的最大值,及此时点P的坐标;
解:∵直线CD的解析式为y=kx+4,
∴与y轴交点坐标C为(0,4),
∵抛物线的顶点坐标为(-3, ),
∴抛物线解析式可设为y=a(x+3)2+ ,
将点C(0,4)代入得a(0+3)2+ =4,
解得a=- ,
∴抛物线解析式为y=- (x+3)2+ ,
即y= .
(2)【思维教练】要求直线CD的解析式,需知点C、D的坐标,结合题意,C点坐标已知,只需求得D点坐标代入解析式即可,由点D是BO的中点,结合抛物线求得B点坐标即可得D点坐标.
解:令y=- x2- x+4=0,
解得x1=-8,x2=2.
∴点A(2,0),点B(-8,0).
∵点D是OB的中点,
∴点D(-4,0),
将点D代入直线y=kx+4得-4k+4=0,
解得k=1,
∴直线CD的解析式为y=x+4.
(3)【思维教练】因为△ACD的AD边在坐标轴上,C点坐标已知,则由S△ADC= ·CO·AD求解即可.
解:∵D(-4,0),A(2,0),∴AD=6,
∵OC=4,∴S△ADC= AD·OC= ×6×4=12.
(4)【思维教练】若PB=PD,则P为BD的垂直平分线与抛物线的交点.
解:当PB=PD,则P点在BD的垂直平分线上,
∵点B(-8,0),点D(-4,0),
∴P点的横坐标为-6,且在抛物线上,
∴y= ,
∴P点的坐标为(-6,4).
(5)【思维教练】要求PA+PC值最小,则可找出点A或C,其中一点关于对称轴的对称点,与另一点连接与对称轴的交点即为所求的P点.
解:由题图知,B点即为A点关于对称轴的对称点,连接BC与对称轴的交点即为所求的点P.
设直线BC的解析式为y=kx+b.
∵点B(-8,0),点C(0,4).
∴ ,解得 ,
∴直线BC的解析式为y= x+4.
∴当x=-3时,y= .
∴P点的坐标为(-3, ).
(6)【思维教练】S△BDP=S△BDC,由三角形的面积公式为 ×底×高,结合题意知△BDP和△BDC的底同为BD,△BDC的高为OC,则只需求得抛物线上点到线段BD的距离等于OC的点即为P点.
解:∵S△BDP=S△BDC,
∴|yP|=yC,即yP=yC=4或yP=-yC=-4.
当yP=yC时,点P与点C关于抛物线对称轴对称,
当yP=-yC=-4时, ,
解得xP=-3± ,
即点P的坐标为(-3- ,-4)或(-3+ ,-4).
综上,满足题意的P点有3个,为(-6,4),
(-3- ,-4),(-3+ ,-4).
∵点C(0,4),对称轴为x=-3,
∴点P的坐标为(-6,4);
(7)①【思维教练】要求△CDP的面积,因为点P的位置不确定,故过点D作DE⊥x轴交抛物线于点E,分点P在点E的左、右两侧进行讨论.因为这两种情况下,△CDP的三条边均不在坐标轴或平行于坐标轴的直线上,故过点P作PG⊥x轴于点G,采用割或补的方法把它转化为易求出面积的图形来求解.
解:过D作DE⊥x轴交抛物线于E.
∵点D(-4,0),
∴点E(-4,6).
如解图①,当点P在BE段抛物线上,
即-8
∵点P的横坐标为t,∴PG= ,
∴S△PCD=S四边形PGOC-S△PGD-S△DOC
=
=
=- t2-5t.
如解图②,当点P在CE段时,-4
综上,S=- t2-5t.
(7)②【思维教练】由①中可知S△CDP关于P点横坐标的函数关系式,若S△CDP的值最大,即用配方法求对应函数的最大值.
解:∵S=- t2-5t=- (t+5)2+ ,
∴当t=-5时,S有最大值,最大值为 .
(7)③【思维教练】若使S△CDP=S△BDP,由①知S△CDP关于t的函数关系式,结合题图BD在x轴上,易求BD的长度和S△BDP关于t的函数关系式,将两函数关系式联立求解即可得t的值,若无解,即不存在这样的t.
解:∵S△BDP= BD·yP= ×4×(- t2- t+4)=- t2-3t+8,
根据题意有- t2-3t+8=- t2-5t,解得t=-4.
即存在t=-4,使S△CDP=S△BDP .
(7)④【思维教练】由题图,PD将四边形CD分成了△BDP和△CDP两部分,且2S△BDP=3S△CDP或3S△BDP=2S△CDP,由①可知S△CDP关于t的函数关系式,由③可得S△BDP关于t的函数关系式,再根据两者之间的等量关系联立求解即可得t的值.
解:根据题意,(1)若2S△BDP=3S△PCD,
则 ,
解得t1=-2,t2=-16(舍),
(2)若3S△BDP=2S△PCD,
则 ,
解得t1=-6,t2=8(舍),
综上,存在这样的t且值分别为-2或-6.
探究三角形或四边形面积的最值问题:
1.可设动点的坐标为(t,at2+bt+c);
2.①求一边在坐标轴上的三角形面积时,取在坐标轴上的线段为底边,则底边上的高为动点的横坐标或纵坐标的绝对值;②求三条均不在坐标轴上的三角形或不规则的四边形面积时,常采用割或补的方法把它转化为易求出面积的图形;
3.用含有未知数的代数式表示出图形的面积;
4.用二次函数的知识来求最大值或最小值时,常采用配方法求解;
解决此类题目需要特别注意点的运动或者图形的变换引起的图形变化,看是否需要进行分类讨论.
二次函数图象的实际应用(难点)
例5 (2016合肥38中一模)音乐喷泉(图①)可以使喷水造型随音乐的节奏变化而变化,某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边20 m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一根根不同的抛物线(图②),这组抛物线的统一形式为y= .
例1题图
(1)若已知k=1,且喷出的抛物线,水线最大高度达3 m,求此时a、b的值;
(1)【思维教练】要求a、b的值,需找出a、b的关系式,由已知k=1可得y=x,由抛物线的顶点y=xt,及水线最大高度为3 m,可得出a、b的关系式,求解即可.
解:(1)∵y= 的顶点为 ,抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3 m,
∴ , ,
解得a= ,b=2,
即k=1,且喷出的抛物线水线最大高度达3 m时a、b的值分别是 、2;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线,水线最大高度是多少?
【思维教练】求水线的最大高度即求抛物线y=ax2+bx的顶点的纵坐标,由已知喷出的水恰好达到岸边,可得抛物线的对称轴,再根据y=ax2+bx 的顶点在直线y=x上求解即可.
(2)∵k=1,喷出的水恰好到岸边,出水口离岸边20 m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=10,y=x=10,
即此时喷出的抛物线,水线最大高度是10米;
(3)若k=2,且要求喷出的抛物线水不能到岸边,求a的取值范围.
【思维教练】求a的取值范围,需找出关于a的不等式,由已知喷出的抛物线水不能到岸边,可得对称轴 ,再结合k=2,抛物线y=ax2+bx的顶点在直线y=2x上可得b值代入不等式求解即可.
(3)∵y=ax2+bx的顶点 在直线y=2x上,
∴ ,解得b=4,
∵喷出的抛物线水线不能到岸边,出水口离岸边20 m,
∴ ,即 ,
解得:a>
例6 圣诞节期间,某商店销售一种圣诞帽,这种帽子每顶进价为10元.销售统计表明,该产品在圣诞节前每天的销售量t(顶)与每件的销售价x(元/顶)之间大致存在关系:t=-2x+80;该产品在圣诞节后每天的销售量p(顶)与每件的销售价x(元/顶)之间大致存在关系:p= (10<x≤20,p取整数).
(1)在圣诞节前这种帽子销售价定为多少元时其销售量为零;
(2)设每天所得的销售利润为y元,分别写出圣诞节前和圣诞节后y与x之间的函数关系式;
(3)求销售价定为多少时,销售利润最大,最大利润是多少?
(1)【思维教练】销售量为零,即t=0,把t=0代入t=-2x+80,求出x的值;
解:∵当t=-2x+80=0时,x=40,
∴在圣诞节前这种帽子销售价定为40元/顶时,其销售量为零;
(2)【思维教练】根据“销售利润=销售量×(销售单价-进货单价)”列出 y与x之间的函数关系式;
解:由题意,得:
①圣诞节前,y=t(x-10)=(-2x+80)(x-10)=-2x2+100x-800;
②圣诞节后,y= (10<x≤20);
(3)【思维教练】根据第(2)问中所求圣诞节前和圣诞节后y与x之间的函数关系式,分别求出圣诞节前与圣诞节后的最大销售利润,两者比较,即可求解.
解:在圣诞节前,y=-2x2+100x-800=-2(x-25)2+450,
∴当x=25时,y有最大值y1,且y1=450;
在圣诞节后,y=400- (10<x≤20, 为整数),
∴当x=20时,y有最大值y2,且y2=200;
∵y1>y2 ,
∴销售价定为25元/顶时,销售利润最大,最大利润是450元 .
谢 谢
