沪科版九年级上册 数学 21.6 综合与实践 获取最大利润课件(17张PPT)
文档属性
| 名称 | 沪科版九年级上册 数学 21.6 综合与实践 获取最大利润课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 626.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览



文档简介
21.6 综合与实践 获取最大利润
你知道吗?
知识点1:什么样的函数是二次函数?
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。
=a(x+ —)2+
2a
b
4ac-b2
4a
y=ax2+bx+c
顶点坐标(- — , )
b
2a
4ac-b2
4a
b
2a
将y=-x2+2x+1写成顶点式__________ 对称轴为_____,顶点为______
对称轴:x=-—
学以至用
2
1
y=-(x+2)2-1
2
1
x=-2
(-2,-1)
知识点2:一般式与顶点式的转化
顶点坐标(- — , )
b
2a
4ac-b2
4a
b
2a
②对称轴:x=- —
x
y
0
x=-
b
2a
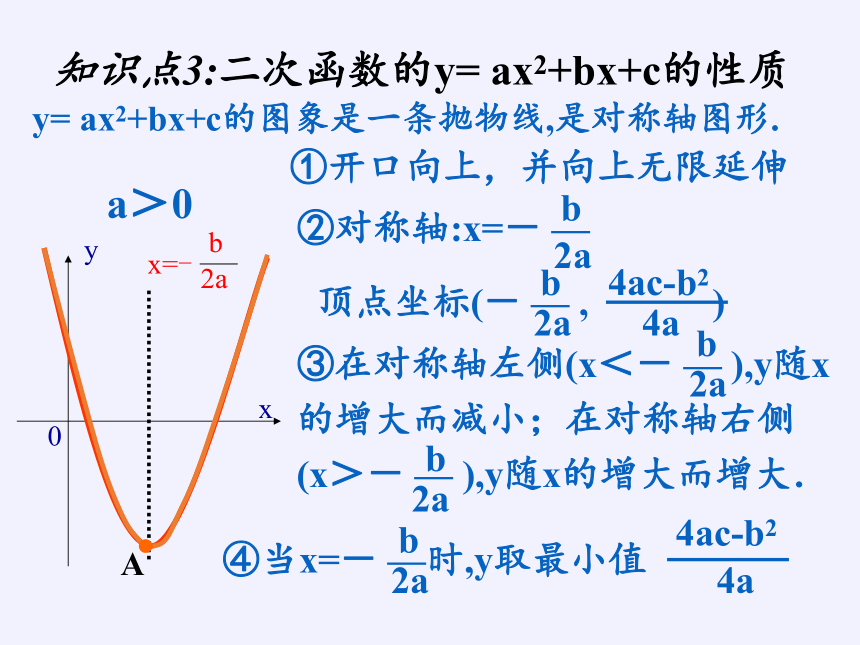
知识点3:二次函数的y= ax2+bx+c的性质
a>0
①开口向上,并向上无限延伸
③在对称轴左侧(x<- — ),y随x的增大而减小;在对称轴右侧 (x>- — ),y随x的增大而增大.
2a
2a
b
b
④当x=- —时,y取最小值
2a
b
4ac-b2
4a
A
y= ax2+bx+c的图象是一条抛物线,是对称轴图形.
顶点坐标(- — , )
b
2a
4ac-b2
4a
b
2a
②对称轴:x=- —
x=-
b
2a
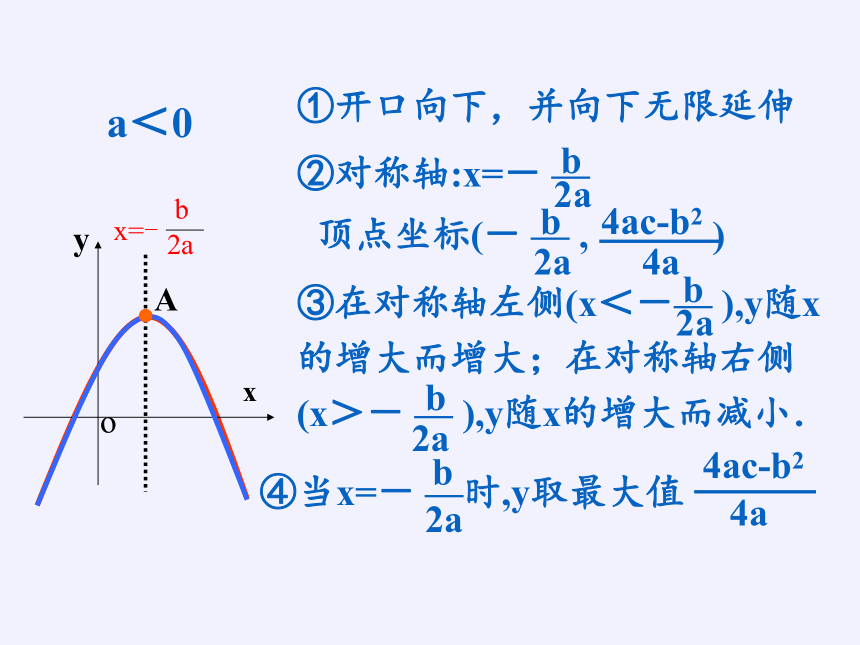
a<0
①开口向下,并向下无限延伸
③在对称轴左侧(x<-— ),y随x的增大而增大;在对称轴右侧 (x>- — ),y随x的增大而减小.
2a
2a
b
b
④当x=- —时,y取最大值
2a
b
4ac-b2
4a
A
y
x
o
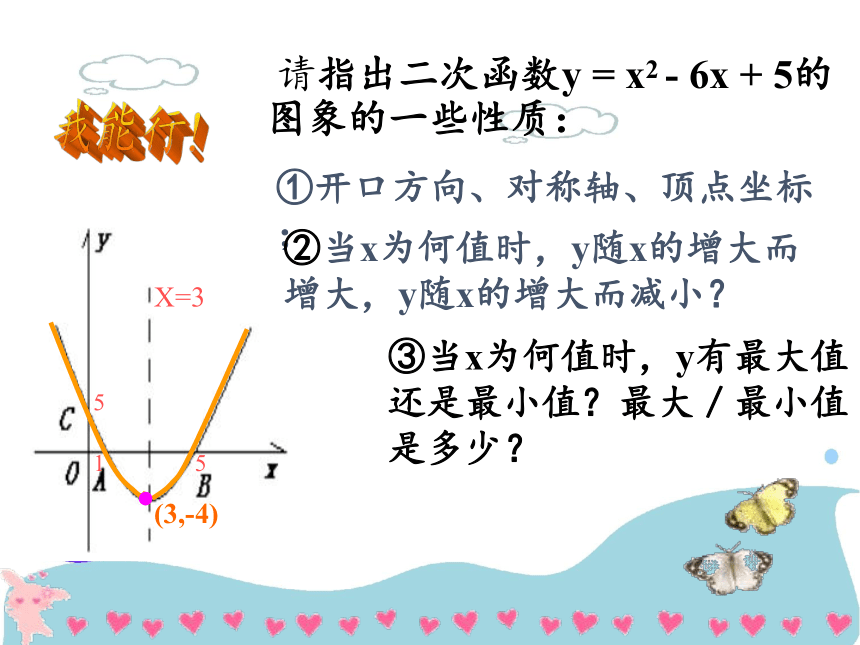
请指出二次函数y = x2 - 6x + 5的图象的一些性质:
1
5
5
X=3
我能行!
①开口方向、对称轴、顶点坐标;
②当x为何值时,y随x的增大而增大,y随x的增大而减小?
③当x为何值时,y有最大值还是最小值?最大/最小值是多少?
(3,-4)
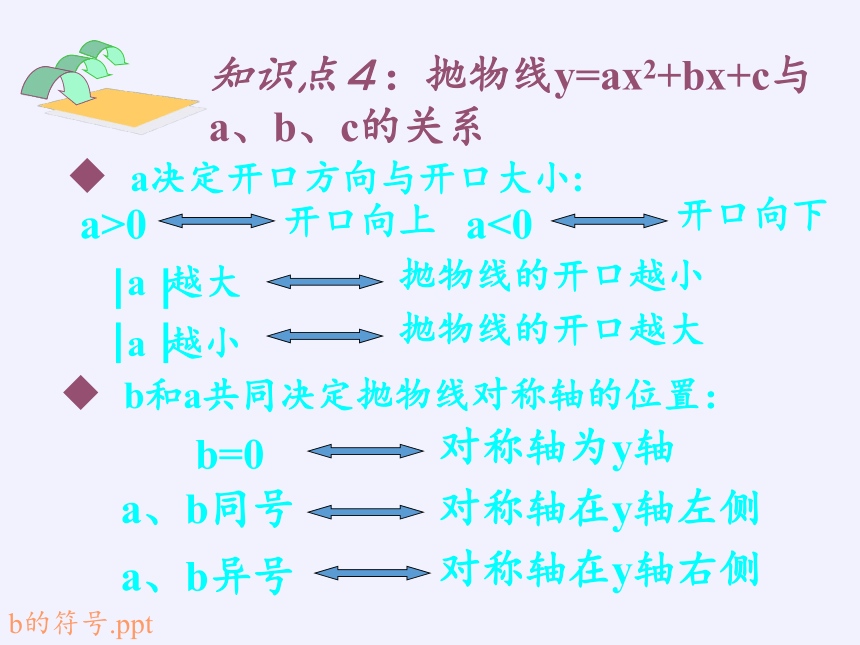
知识点4:抛物线y=ax2+bx+c与a、b、c的关系
a决定开口方向与开口大小:
b和a共同决定抛物线对称轴的位置:
b的符号.ppt
抛物线的开口越大
a>0
开口向上
a<0
开口向下
a 越大
抛物线的开口越小
a 越小
b=0
对称轴为y轴
a、b同号
对称轴在y轴左侧
a、b异号
对称轴在y轴右侧
c的大小决定抛物线与y轴交点的位置:.
c的符号.ppt
c=0
抛物线经过原点
c>0
抛物线与y轴交于正半轴
c<0
抛物线与y轴交于负半轴
y=ax2
二次函数y=2x2如何平移得到二次函数y=2(x-1)2+2?
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
议一议
平移.ppt
知识点5:二次函数图象的平移
向上(k>0)或向下(k<0)平移 k 个单位
y=ax2
顶点(0,0)
y=ax2+k顶点(0,k)
y=a(x-h)2+k顶点(h,k)
向左(h<0)或向右(h>0)平移 h 个单位
向左(h<0)或向右(h>0)平移 h 个单位
向上(k>0)或向下(k<0)平移 k 个单位
y=a(x-h)2顶点(h,0)
知识点6:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象是一条抛物线,是轴对称图形,那该如何画出抛物线呢?
具体方法:⑴求顶点坐标和对称轴;
⑵列表;⑶描点;(4)再将各点用平滑的曲线连起来.
画出二次函数y=-x2-x--的图象
X
-3
-1
1
3
5
y= -x2-x--
6
0
-2
0
6
画抛物线.gsp
1
3
2
2
2
1
3
2
1.已知二次函数y=ax2+bx+c(a≠0),其中a、b、c满足a+b+c=0和9a-3b+c=0,则该二次函数图象的对称轴是_______
x=-1
2.抛物线y=-2x2-4x-5经过平移得到
y=-2x2,平移方法是( )
A.向左平移1个单位,再向下平移3个单位.
B.向左平移1个单位,再向上平移3个单位.
C.向右平移1个单位,再向下平移3个单位.
D.向右平移1个单位,再向上平移3个单位.
D
例2.ppt
3.若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2-mx( )
A.有最大值- B.有最大值--
C.有最小值- D.有最小值--
m
m
m
m
4
4
4
4
B
4.若A(- 4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1、y2、y3的大小关系是( )
A. y1 C. y3B
例4.ppt
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc < 0 ②a+b+c > 0③a+c > b④4a-2b+c<0 其中正确结论的序号是__________
1
-1
0
x
y
①②④
这节课你有那些收获?
复习了二次函数的图象和性质,通过巩固练习,加深理解了二次函数的图象和性质,解决了一些相关的应用问题。
复习了二次函数图象的平移问题,知道了y=ax2 、y=ax2+k 、y=a(x-h)2 与y=a(x-h)2 +k如何平移。
回顾了用描点法画二次函数的图象
归纳小结
如图,已知二次函数y=ax2+bx+c的顶点坐标是 C(-1,-2),且过点 A(-3,0) (1)求a+b+c的值
0
x
C
A
(2)当x为何值时,y随x的增大而减小,x为何值时,y有最大(小)值,最大(小)值是多少?
(3)-2≤x≤1时,y的取值范围?
B
y
D
课后作业
谢 谢
你知道吗?
知识点1:什么样的函数是二次函数?
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。
=a(x+ —)2+
2a
b
4ac-b2
4a
y=ax2+bx+c
顶点坐标(- — , )
b
2a
4ac-b2
4a
b
2a
将y=-x2+2x+1写成顶点式__________ 对称轴为_____,顶点为______
对称轴:x=-—
学以至用
2
1
y=-(x+2)2-1
2
1
x=-2
(-2,-1)
知识点2:一般式与顶点式的转化
顶点坐标(- — , )
b
2a
4ac-b2
4a
b
2a
②对称轴:x=- —
x
y
0
x=-
b
2a
知识点3:二次函数的y= ax2+bx+c的性质
a>0
①开口向上,并向上无限延伸
③在对称轴左侧(x<- — ),y随x的增大而减小;在对称轴右侧 (x>- — ),y随x的增大而增大.
2a
2a
b
b
④当x=- —时,y取最小值
2a
b
4ac-b2
4a
A
y= ax2+bx+c的图象是一条抛物线,是对称轴图形.
顶点坐标(- — , )
b
2a
4ac-b2
4a
b
2a
②对称轴:x=- —
x=-
b
2a
a<0
①开口向下,并向下无限延伸
③在对称轴左侧(x<-— ),y随x的增大而增大;在对称轴右侧 (x>- — ),y随x的增大而减小.
2a
2a
b
b
④当x=- —时,y取最大值
2a
b
4ac-b2
4a
A
y
x
o
请指出二次函数y = x2 - 6x + 5的图象的一些性质:
1
5
5
X=3
我能行!
①开口方向、对称轴、顶点坐标;
②当x为何值时,y随x的增大而增大,y随x的增大而减小?
③当x为何值时,y有最大值还是最小值?最大/最小值是多少?
(3,-4)
知识点4:抛物线y=ax2+bx+c与a、b、c的关系
a决定开口方向与开口大小:
b和a共同决定抛物线对称轴的位置:
b的符号.ppt
抛物线的开口越大
a>0
开口向上
a<0
开口向下
a 越大
抛物线的开口越小
a 越小
b=0
对称轴为y轴
a、b同号
对称轴在y轴左侧
a、b异号
对称轴在y轴右侧
c的大小决定抛物线与y轴交点的位置:.
c的符号.ppt
c=0
抛物线经过原点
c>0
抛物线与y轴交于正半轴
c<0
抛物线与y轴交于负半轴
y=ax2
二次函数y=2x2如何平移得到二次函数y=2(x-1)2+2?
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
议一议
平移.ppt
知识点5:二次函数图象的平移
向上(k>0)或向下(k<0)平移 k 个单位
y=ax2
顶点(0,0)
y=ax2+k顶点(0,k)
y=a(x-h)2+k顶点(h,k)
向左(h<0)或向右(h>0)平移 h 个单位
向左(h<0)或向右(h>0)平移 h 个单位
向上(k>0)或向下(k<0)平移 k 个单位
y=a(x-h)2顶点(h,0)
知识点6:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象是一条抛物线,是轴对称图形,那该如何画出抛物线呢?
具体方法:⑴求顶点坐标和对称轴;
⑵列表;⑶描点;(4)再将各点用平滑的曲线连起来.
画出二次函数y=-x2-x--的图象
X
-3
-1
1
3
5
y= -x2-x--
6
0
-2
0
6
画抛物线.gsp
1
3
2
2
2
1
3
2
1.已知二次函数y=ax2+bx+c(a≠0),其中a、b、c满足a+b+c=0和9a-3b+c=0,则该二次函数图象的对称轴是_______
x=-1
2.抛物线y=-2x2-4x-5经过平移得到
y=-2x2,平移方法是( )
A.向左平移1个单位,再向下平移3个单位.
B.向左平移1个单位,再向上平移3个单位.
C.向右平移1个单位,再向下平移3个单位.
D.向右平移1个单位,再向上平移3个单位.
D
例2.ppt
3.若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2-mx( )
A.有最大值- B.有最大值--
C.有最小值- D.有最小值--
m
m
m
m
4
4
4
4
B
4.若A(- 4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1、y2、y3的大小关系是( )
A. y1
例4.ppt
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc < 0 ②a+b+c > 0③a+c > b④4a-2b+c<0 其中正确结论的序号是__________
1
-1
0
x
y
①②④
这节课你有那些收获?
复习了二次函数的图象和性质,通过巩固练习,加深理解了二次函数的图象和性质,解决了一些相关的应用问题。
复习了二次函数图象的平移问题,知道了y=ax2 、y=ax2+k 、y=a(x-h)2 与y=a(x-h)2 +k如何平移。
回顾了用描点法画二次函数的图象
归纳小结
如图,已知二次函数y=ax2+bx+c的顶点坐标是 C(-1,-2),且过点 A(-3,0) (1)求a+b+c的值
0
x
C
A
(2)当x为何值时,y随x的增大而减小,x为何值时,y有最大(小)值,最大(小)值是多少?
(3)-2≤x≤1时,y的取值范围?
B
y
D
课后作业
谢 谢
