沪科版九年级上册 数学 课件 22.3 相似三角形的性质(20张)
文档属性
| 名称 | 沪科版九年级上册 数学 课件 22.3 相似三角形的性质(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 570.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 20:56:42 | ||
图片预览





文档简介
22.3 相似三角形的性质
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
复习
相似三角形的性质
成比例
相等
相似比
相似比
1、相似三角形对应边________,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
相似比的平方
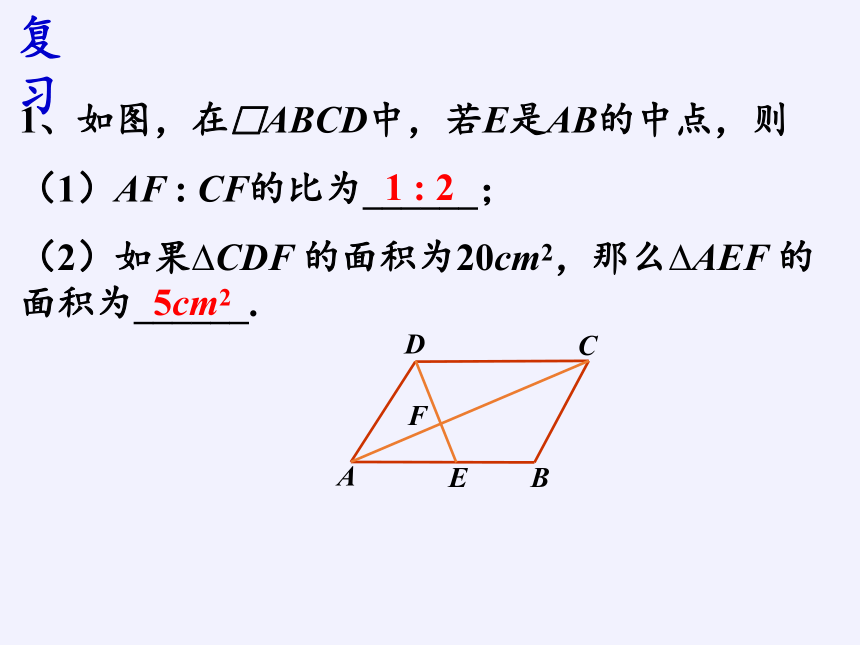
1、如图,在□ABCD中,若E是AB的中点,则
(1)AF : CF的比为______;
(2)如果?CDF 的面积为20cm2,那么?AEF 的面积为______.
B
F
E
D
C
A
1 : 2
5cm2
复习
复习
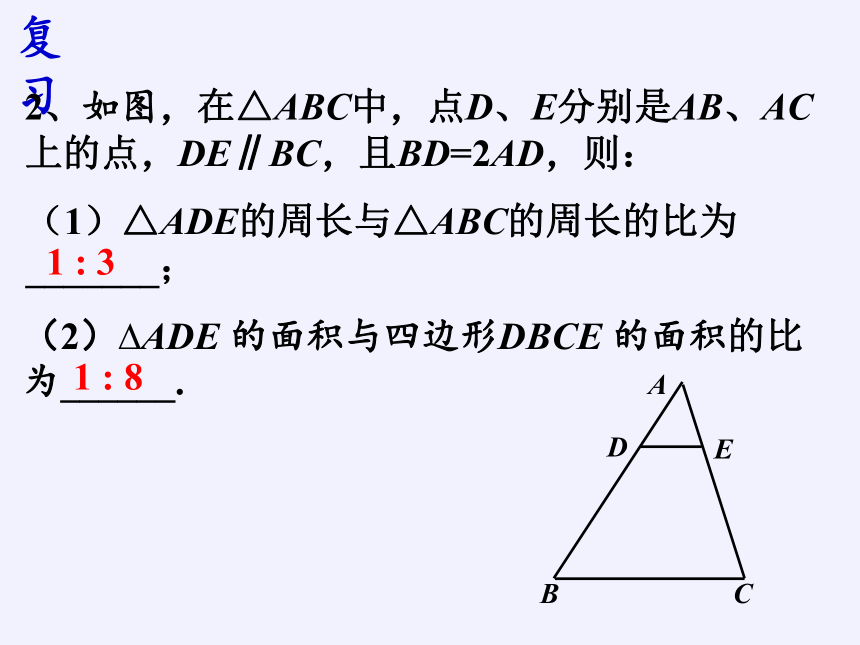
(1)△ADE的周长与△ABC的周长的比为 _______;
(2)?ADE 的面积与四边形DBCE 的面积的比为______.
1 : 8
A
B
C
E
D
1 : 3
2、如图,在△ABC中,点D、E分别是AB、AC 上的点,DE∥BC,且BD=2AD,则:
3、在比例尺为 1∶500 的地图上,测得一块三
角形地ABC的周长为12 cm,面积为6 cm2,则这
块地的实际周长是______m ,面积_______m2.
复习
60
150
A
B
C
D
E
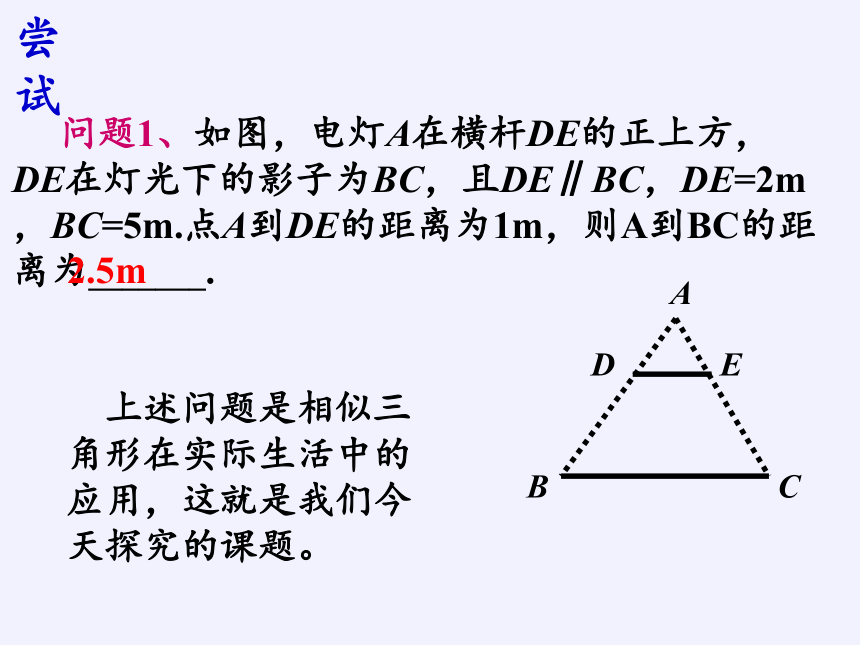
问题1、如图,电灯A在横杆DE的正上方, DE在灯光下的影子为BC,且DE∥BC,DE=2m,BC=5m.点A到DE的距离为1m,则A到BC的距离为_______.
2.5m
尝试
上述问题是相似三角形在实际生活中的应用,这就是我们今天探究的课题。
运用相似三角形解决实际问题时,首先将实际问题转化为________问题,然后用相似三角形的性质进行求解.
数 学
相似三角形的应用
新课
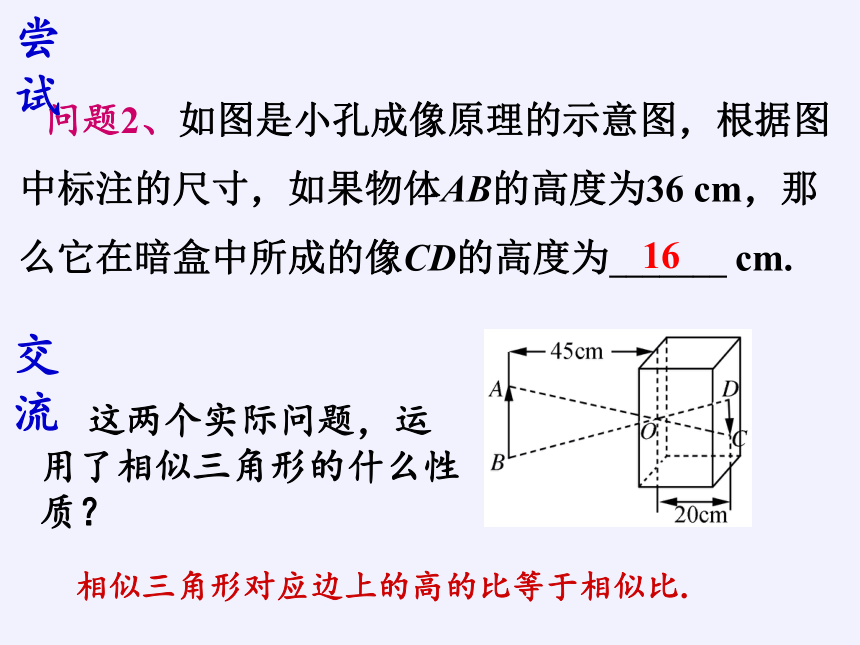
问题2、如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36 cm,那么它在暗盒中所成的像CD的高度为_______ cm.
16
这两个实际问题,运用了相似三角形的什么性质?
交流
相似三角形对应边上的高的比等于相似比.
尝试
尝试
问题3、小虎的身高为1.6m,他的影长为2m,同一时刻他测得电线杆的影长为18m,则此电线杆的高度为 ( )
A. 20m B. 14.4m C. 16.4m D. 15.4m
B
范例
问题4、李勇想利用树影测量树高.他在某一时刻测得长为1 m的竹竿影长为0.9 m,然后再测量树影,因树靠 近一幢建筑物,影子有一部分影子在墙上(如图),测 得留在墙上影高CD=1.2 m,地面部分的影长BC=2.7m. 问这棵树的高度是多少?
A
B
C
D
E
解:延长AD交BC的延长线于点E.
∵CD:CE=1:0.9 ,
∴CE=1.2×0.9=1.08(m).
∵AB:BE=1:0.9,
∴AB=BE/0.9=4.2(m).
答:这棵树的高度是4.2m.
∴BE=BC+CE=3.78(m).
方法一
A
B
C
D
F
答:这棵树的高度是4.2m.
∴AB=AF+FB
=3+1.2=4.2(m).
解:过点D作DF⊥AB于点F.
∵AF:FD=1:0.9 ,
∴AF=3m,
范例
FD=BC=2.7m,BF=CD=1.2m,
问题4、李勇想利用树影测量树高.他在某一时刻测得长为1 m的竹竿影长为0.9 m,然后再测量树影,因树靠 近一幢建筑物,影子有一部分影子在墙上(如图),测 得留在墙上影高CD=1.2 m,地面部分的影长BC=2.7m. 问这棵树的高度是多少?
方法二
练习
解:∵∠DEF=∠DCB=900,
∴△DCB ∽△DEF,
∴ CB :DC = EF :DE,
∴ CB=4,
∴AB=1.5+4=5.5(m).
问题5、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜 边DF保持水平,并且边DE与点B在同一直线上,已知 纸板的两条直角边DE=40 cm,EF=20cm,测得边DF离 地面的高度AC=1.5 m,CD=8m,问树高AB是多少?
∠D=∠D,
答:这棵树的高度是5.5m.
探究
问题6、如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆约30 m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上12 cm的长度恰好遮住电线杆.已知臂长为60 cm,求电线杆的高.
DF=0.6 m,GF=0.12m,EC=30m.
分析:已知:AE⊥EC,DF⊥AE,
GF⊥EC,BC⊥EC,
求: BC的长.
探究
探究
∵GF⊥EC, BC⊥EC, ∴GF∥BC, ∴AM⊥GF.
解:过点A作AN⊥BC于点N,
交GF于点M.
N
M
∴△ABC ∽△AGF, ∴BC :AN=GF : AM.
(相似三角形对应高的比等于相似比)
∴BC :30=0.12 :0.6, ∴BC=6m.
∵ AN=EC=30, AM=DF=0.6,
答:电线杆的高为6 m.
通过这节课的学习,我知道了………,我能………, 还能………, 同时,我还感受到……….
实际问题
数学问题的解
实际问题
的答案
数学问题
几何、方程
画图、分析
求 解
检验
知识 方法 步骤 联系 思想
小结
课本 P102~P104
22.5 综合与实践——测量与误差
实践
Ⅰ. 课 本
P92习题 15.
P107 A组复习题
11. 12. 13.
Ⅱ. 《同步练习》
P68~P71练习(三)、(拓展)
作业
祝同学们学习进步
谢 谢
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
复习
相似三角形的性质
成比例
相等
相似比
相似比
1、相似三角形对应边________,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
相似比的平方
1、如图,在□ABCD中,若E是AB的中点,则
(1)AF : CF的比为______;
(2)如果?CDF 的面积为20cm2,那么?AEF 的面积为______.
B
F
E
D
C
A
1 : 2
5cm2
复习
复习
(1)△ADE的周长与△ABC的周长的比为 _______;
(2)?ADE 的面积与四边形DBCE 的面积的比为______.
1 : 8
A
B
C
E
D
1 : 3
2、如图,在△ABC中,点D、E分别是AB、AC 上的点,DE∥BC,且BD=2AD,则:
3、在比例尺为 1∶500 的地图上,测得一块三
角形地ABC的周长为12 cm,面积为6 cm2,则这
块地的实际周长是______m ,面积_______m2.
复习
60
150
A
B
C
D
E
问题1、如图,电灯A在横杆DE的正上方, DE在灯光下的影子为BC,且DE∥BC,DE=2m,BC=5m.点A到DE的距离为1m,则A到BC的距离为_______.
2.5m
尝试
上述问题是相似三角形在实际生活中的应用,这就是我们今天探究的课题。
运用相似三角形解决实际问题时,首先将实际问题转化为________问题,然后用相似三角形的性质进行求解.
数 学
相似三角形的应用
新课
问题2、如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36 cm,那么它在暗盒中所成的像CD的高度为_______ cm.
16
这两个实际问题,运用了相似三角形的什么性质?
交流
相似三角形对应边上的高的比等于相似比.
尝试
尝试
问题3、小虎的身高为1.6m,他的影长为2m,同一时刻他测得电线杆的影长为18m,则此电线杆的高度为 ( )
A. 20m B. 14.4m C. 16.4m D. 15.4m
B
范例
问题4、李勇想利用树影测量树高.他在某一时刻测得长为1 m的竹竿影长为0.9 m,然后再测量树影,因树靠 近一幢建筑物,影子有一部分影子在墙上(如图),测 得留在墙上影高CD=1.2 m,地面部分的影长BC=2.7m. 问这棵树的高度是多少?
A
B
C
D
E
解:延长AD交BC的延长线于点E.
∵CD:CE=1:0.9 ,
∴CE=1.2×0.9=1.08(m).
∵AB:BE=1:0.9,
∴AB=BE/0.9=4.2(m).
答:这棵树的高度是4.2m.
∴BE=BC+CE=3.78(m).
方法一
A
B
C
D
F
答:这棵树的高度是4.2m.
∴AB=AF+FB
=3+1.2=4.2(m).
解:过点D作DF⊥AB于点F.
∵AF:FD=1:0.9 ,
∴AF=3m,
范例
FD=BC=2.7m,BF=CD=1.2m,
问题4、李勇想利用树影测量树高.他在某一时刻测得长为1 m的竹竿影长为0.9 m,然后再测量树影,因树靠 近一幢建筑物,影子有一部分影子在墙上(如图),测 得留在墙上影高CD=1.2 m,地面部分的影长BC=2.7m. 问这棵树的高度是多少?
方法二
练习
解:∵∠DEF=∠DCB=900,
∴△DCB ∽△DEF,
∴ CB :DC = EF :DE,
∴ CB=4,
∴AB=1.5+4=5.5(m).
问题5、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜 边DF保持水平,并且边DE与点B在同一直线上,已知 纸板的两条直角边DE=40 cm,EF=20cm,测得边DF离 地面的高度AC=1.5 m,CD=8m,问树高AB是多少?
∠D=∠D,
答:这棵树的高度是5.5m.
探究
问题6、如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆约30 m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上12 cm的长度恰好遮住电线杆.已知臂长为60 cm,求电线杆的高.
DF=0.6 m,GF=0.12m,EC=30m.
分析:已知:AE⊥EC,DF⊥AE,
GF⊥EC,BC⊥EC,
求: BC的长.
探究
探究
∵GF⊥EC, BC⊥EC, ∴GF∥BC, ∴AM⊥GF.
解:过点A作AN⊥BC于点N,
交GF于点M.
N
M
∴△ABC ∽△AGF, ∴BC :AN=GF : AM.
(相似三角形对应高的比等于相似比)
∴BC :30=0.12 :0.6, ∴BC=6m.
∵ AN=EC=30, AM=DF=0.6,
答:电线杆的高为6 m.
通过这节课的学习,我知道了………,我能………, 还能………, 同时,我还感受到……….
实际问题
数学问题的解
实际问题
的答案
数学问题
几何、方程
画图、分析
求 解
检验
知识 方法 步骤 联系 思想
小结
课本 P102~P104
22.5 综合与实践——测量与误差
实践
Ⅰ. 课 本
P92习题 15.
P107 A组复习题
11. 12. 13.
Ⅱ. 《同步练习》
P68~P71练习(三)、(拓展)
作业
祝同学们学习进步
谢 谢
