华东师大版七年级上册 数学 课件 2.5 有理数的大小比较(14张)
文档属性
| 名称 | 华东师大版七年级上册 数学 课件 2.5 有理数的大小比较(14张) |  | |
| 格式 | pptx | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 21:00:28 | ||
图片预览






文档简介
导入新课
回顾与思考
问题1:如何在数轴上比较两个有理数的大小?
由数轴的知识我们知道:
(1)在数轴上表示的两个数,__边的数总比___边的数大。
左
右
(2)正数都_____零,负数都_____零。
大于
小于
(3)正数_____负数。
大于
那么,如何比较两个负数的大小呢?
2.5 有理数的大小比较
第2章 有理数
导入新课
讲授新课
当堂练习
课堂小结
有理数的大小比较
问题1 在数轴上分别画出下列各对数,并比较它们的大小.
(1)-1与-3; (2)-5与-2.
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
问题引导
(1)-3< -1;
(2)-5< -2.
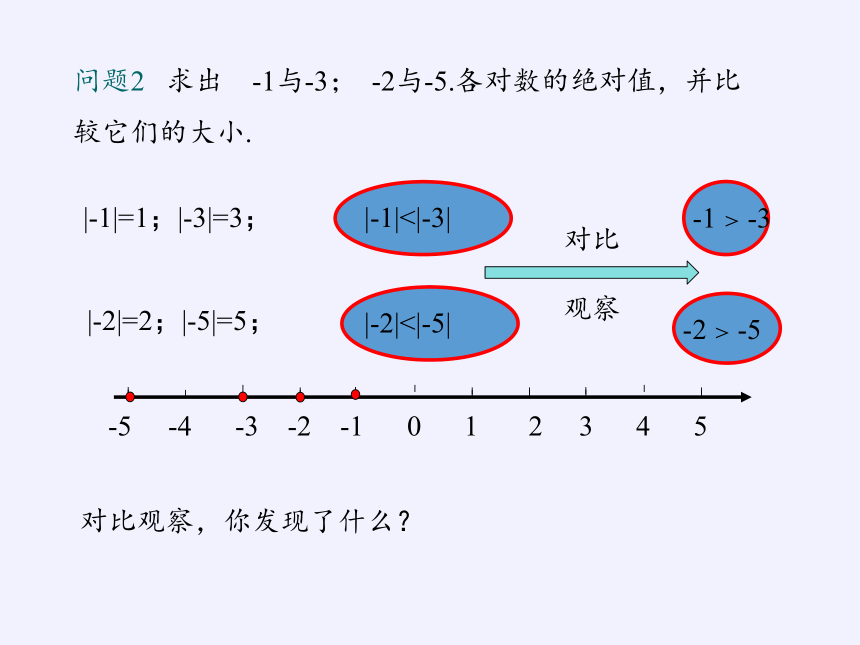
问题2 求出 -1与-3; -2与-5.各对数的绝对值,并比较它们的大小.
|-1|=1;|-3|=3;
|-1|<|-3|
|-2|=2;|-5|=5;
|-2|<|-5|
-2 > -5
-1 > -3
对比
观察
-5 -4 -3 -2 -1 0 1 2 3 4 5
对比观察,你发现了什么?
法则:两个负数,绝对值大的反而小.
总结归纳
两个负数比较大小的一般步骤:
①求绝对值;
②比较绝对值的大小;
③比较负数的大小.
例1: 比较 的大小。
解:
(1)先分别求出它们的绝对值,并比较其大小
∵
(2)根据“两个负数,绝对值大的数反而小”,得出结论).
∴
∴
精析典例
例2 比较下列各对数的大小
.
解:(1)这是两个负数比较大小,因为
且1>0.01,
所以-1<-0.01;
(2)化简
因为负数小于0,
所以
(4)
(3)分别化简两数,得
因为正数大于负数,所以
(4)解:两个负数做比较,先求它们的绝对值
比较有理数大小的法则
1.一个数与0比较,要考虑这个数的正负.
正数大于0,0大于负数.
2.异号两数比较,要考虑这两个数的正负.
正数大于负数.
3.同号两数比较,要考虑这两个数的绝对值.
对于两个正数,绝对值大的数大.
对于两个负数,绝对值大的数反而小.
.
注意:需要化简时,要先化简再比较.
总结归纳
有理数大小的比较方法:
一、数轴比较法:
二、直接比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
|
|
|
|
|
|
|
|
|
-5 -4 -3 -2 -1 0 1 2 3
注:多个有理数比较,适宜用数轴.
利用有理数的比较法则进行比较
小试牛刀
比较下面各对数的大小,并说明理由:
⑴ 与 ;
⑵-3 与 +1;
⑶ -1 与 0;
⑷- 与 -
> ,两个正数比较大小,绝对值大的数大
+1> -3, 正数大于一切负数
-1<0, 负数都小于零
- < - , 两个负数比较大小,绝对值大的数反而小
有理数大小的比较方法:
一、数轴比较法:
二、直接比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
|
|
|
|
|
|
|
|
|
-5 -4 -3 -2 -1 0 1 2 3
注:多个有理数比较,适宜用数轴.
利用有理数的比较法则进行比较
课堂小结
谢 谢
回顾与思考
问题1:如何在数轴上比较两个有理数的大小?
由数轴的知识我们知道:
(1)在数轴上表示的两个数,__边的数总比___边的数大。
左
右
(2)正数都_____零,负数都_____零。
大于
小于
(3)正数_____负数。
大于
那么,如何比较两个负数的大小呢?
2.5 有理数的大小比较
第2章 有理数
导入新课
讲授新课
当堂练习
课堂小结
有理数的大小比较
问题1 在数轴上分别画出下列各对数,并比较它们的大小.
(1)-1与-3; (2)-5与-2.
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
问题引导
(1)-3< -1;
(2)-5< -2.
问题2 求出 -1与-3; -2与-5.各对数的绝对值,并比较它们的大小.
|-1|=1;|-3|=3;
|-1|<|-3|
|-2|=2;|-5|=5;
|-2|<|-5|
-2 > -5
-1 > -3
对比
观察
-5 -4 -3 -2 -1 0 1 2 3 4 5
对比观察,你发现了什么?
法则:两个负数,绝对值大的反而小.
总结归纳
两个负数比较大小的一般步骤:
①求绝对值;
②比较绝对值的大小;
③比较负数的大小.
例1: 比较 的大小。
解:
(1)先分别求出它们的绝对值,并比较其大小
∵
(2)根据“两个负数,绝对值大的数反而小”,得出结论).
∴
∴
精析典例
例2 比较下列各对数的大小
.
解:(1)这是两个负数比较大小,因为
且1>0.01,
所以-1<-0.01;
(2)化简
因为负数小于0,
所以
(4)
(3)分别化简两数,得
因为正数大于负数,所以
(4)解:两个负数做比较,先求它们的绝对值
比较有理数大小的法则
1.一个数与0比较,要考虑这个数的正负.
正数大于0,0大于负数.
2.异号两数比较,要考虑这两个数的正负.
正数大于负数.
3.同号两数比较,要考虑这两个数的绝对值.
对于两个正数,绝对值大的数大.
对于两个负数,绝对值大的数反而小.
.
注意:需要化简时,要先化简再比较.
总结归纳
有理数大小的比较方法:
一、数轴比较法:
二、直接比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
|
|
|
|
|
|
|
|
|
-5 -4 -3 -2 -1 0 1 2 3
注:多个有理数比较,适宜用数轴.
利用有理数的比较法则进行比较
小试牛刀
比较下面各对数的大小,并说明理由:
⑴ 与 ;
⑵-3 与 +1;
⑶ -1 与 0;
⑷- 与 -
> ,两个正数比较大小,绝对值大的数大
+1> -3, 正数大于一切负数
-1<0, 负数都小于零
- < - , 两个负数比较大小,绝对值大的数反而小
有理数大小的比较方法:
一、数轴比较法:
二、直接比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
|
|
|
|
|
|
|
|
|
-5 -4 -3 -2 -1 0 1 2 3
注:多个有理数比较,适宜用数轴.
利用有理数的比较法则进行比较
课堂小结
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
