华东师大版七年级上册 数学 课件 4.6.2角的比较和运算(14张)
文档属性
| 名称 | 华东师大版七年级上册 数学 课件 4.6.2角的比较和运算(14张) |  | |
| 格式 | pptx | ||
| 文件大小 | 216.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 21:11:27 | ||
图片预览





文档简介
角的比较和运算
学习目标:
1.通过操作、度量等方式,理解角平分线的意义。
2.会用符号语言表示角平分线的意义
3.能运用角的平分线的意义,进行相关计算,解决简单的几何问题.
学习重点
角平分线的意义及其表示。
学习难点
运用角的平分线的意义,进行相关计算,解决简单的几何问题.
一、 复习提问
1、什么叫线段的中点?
2、如图点C为线段AB的中点
A
B
·
C
请用符号语言表示出来。
(1)AC=BC(相等) (2)AB=2AC AB=2BC (二倍)
(3)AC=BC= AB (一半)
3.什么叫做角?如何表示?
4.取一张纸,请任意裁一个角,并将其表示出来。如:
A
O
B
一、 复习提问
二、自学质疑
1、什么是角的平分线?
2、你有几种办法得到一个角的平分线?
阅读教材P151页,思考问题:
三、小组交流
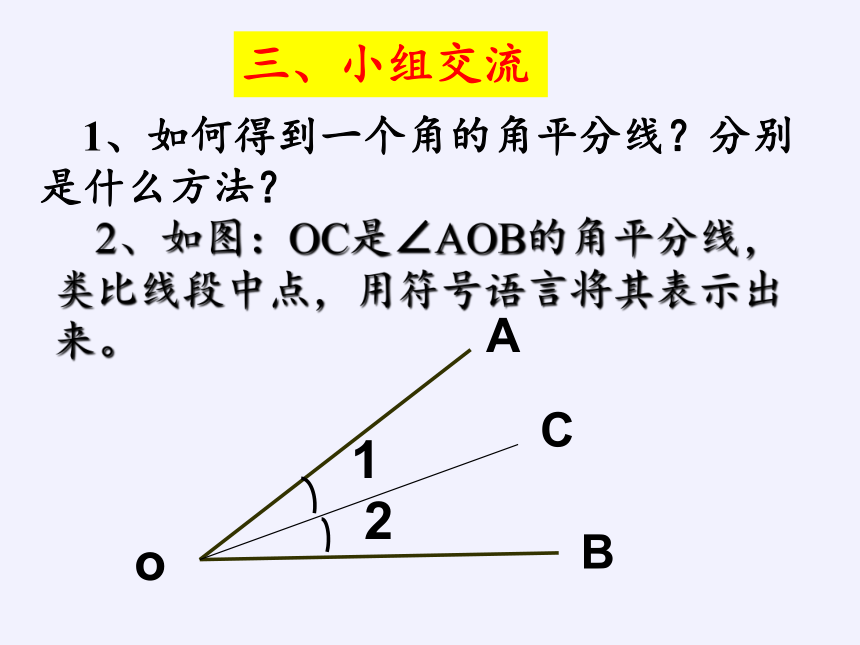
1、如何得到一个角的角平分线?分别是什么方法?
2、如图:OC是∠AOB的角平分线,类比线段中点,用符号语言将其表示出来。
o
B
C
A
1
2
四、展示点拨
1、角的平分线的定义:
从一个角的顶点引出一条射线,把一个角分成相等的两个角,这条射线叫做这个角的平分线。
2、得到一个角的角平分线的方法:
(1)折叠法 ( 2)度量法 (3)尺规作图法。
A
B
M
N
C
0
温馨提示:
作角平分线是最基本的尺规作图,大家一定要掌握噢!
3.用尺规作图法:作已知角的平分线的方法
已知:∠AOB.
求作:∠AOB的平分线.
四、展示点拨
四、展示点拨
4、如何用符号语言表示
角的平分线(如图)
o
B
C
A
1
2
(1)∠1=∠2(相等)
(2)∠1=∠2= ∠AOB(一半)
(3) ∠AOB=2∠1=2∠2(二倍)
1、口答:(1)已知,OC是∠AOB的平分线,若∠AOB=42°。
则∠AOC=( )
∠BOC=( )。
A
O
B
五、训练拓展
C
(2)若∠AOC=20°。
求:∠AOB=( )。
2、计算:
已知:OC是∠AOB的平分线,OE是∠AOD的平分线若,∠AOB=40°,∠AOD=80°。求:∠COE的度数。
五、训练拓展
C
A
O
B
D
E
3、拓展:
已知:OC是∠AOB的平分线,OD是∠AOE的平分线,∠EOB是一个平角。求:∠DOC的度数。
A
O
B
五、训练拓展
C
D
E
六、小结反思
谢 谢
学习目标:
1.通过操作、度量等方式,理解角平分线的意义。
2.会用符号语言表示角平分线的意义
3.能运用角的平分线的意义,进行相关计算,解决简单的几何问题.
学习重点
角平分线的意义及其表示。
学习难点
运用角的平分线的意义,进行相关计算,解决简单的几何问题.
一、 复习提问
1、什么叫线段的中点?
2、如图点C为线段AB的中点
A
B
·
C
请用符号语言表示出来。
(1)AC=BC(相等) (2)AB=2AC AB=2BC (二倍)
(3)AC=BC= AB (一半)
3.什么叫做角?如何表示?
4.取一张纸,请任意裁一个角,并将其表示出来。如:
A
O
B
一、 复习提问
二、自学质疑
1、什么是角的平分线?
2、你有几种办法得到一个角的平分线?
阅读教材P151页,思考问题:
三、小组交流
1、如何得到一个角的角平分线?分别是什么方法?
2、如图:OC是∠AOB的角平分线,类比线段中点,用符号语言将其表示出来。
o
B
C
A
1
2
四、展示点拨
1、角的平分线的定义:
从一个角的顶点引出一条射线,把一个角分成相等的两个角,这条射线叫做这个角的平分线。
2、得到一个角的角平分线的方法:
(1)折叠法 ( 2)度量法 (3)尺规作图法。
A
B
M
N
C
0
温馨提示:
作角平分线是最基本的尺规作图,大家一定要掌握噢!
3.用尺规作图法:作已知角的平分线的方法
已知:∠AOB.
求作:∠AOB的平分线.
四、展示点拨
四、展示点拨
4、如何用符号语言表示
角的平分线(如图)
o
B
C
A
1
2
(1)∠1=∠2(相等)
(2)∠1=∠2= ∠AOB(一半)
(3) ∠AOB=2∠1=2∠2(二倍)
1、口答:(1)已知,OC是∠AOB的平分线,若∠AOB=42°。
则∠AOC=( )
∠BOC=( )。
A
O
B
五、训练拓展
C
(2)若∠AOC=20°。
求:∠AOB=( )。
2、计算:
已知:OC是∠AOB的平分线,OE是∠AOD的平分线若,∠AOB=40°,∠AOD=80°。求:∠COE的度数。
五、训练拓展
C
A
O
B
D
E
3、拓展:
已知:OC是∠AOB的平分线,OD是∠AOE的平分线,∠EOB是一个平角。求:∠DOC的度数。
A
O
B
五、训练拓展
C
D
E
六、小结反思
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
