华东师大版七年级上册 数学 课件 4.1 生活中的立体图形(20张)
文档属性
| 名称 | 华东师大版七年级上册 数学 课件 4.1 生活中的立体图形(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 21:18:00 | ||
图片预览








文档简介
4.1 生活中的立体图形
1.通过观察认识到我们周围的规则物体能找到与他们相似的立体图形;
2.能正确识别柱体、椎体、球体……;
3.认识伟大的数学家欧拉和他的欧拉公式。
4.正确理解点、线、面是构成几何图形的基本元素,正确
理解点、线、面的关系.
自 主 学 习
1
课 堂 研 讨
2
合 作 交 流
3
拓 展 延 伸
4
归 纳 小 结
5
生活中你会经常看见很多实物,由下列实物能想象出
你熟悉的几何体吗?
返回
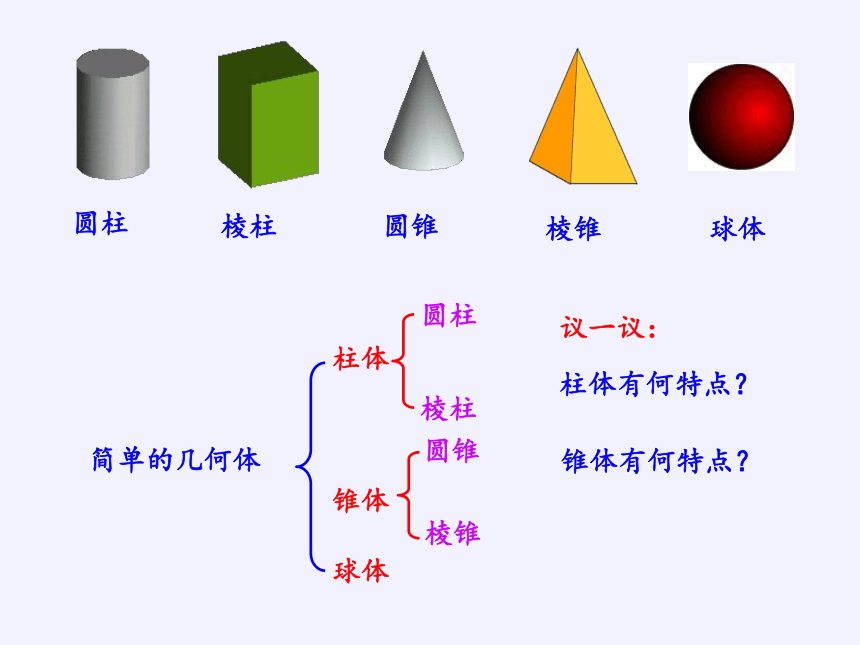
简单的几何体
柱体
锥体
球体
圆柱
棱柱
圆锥
棱锥
议一议:
柱体有何特点?
锥体有何特点?
棱柱
圆柱
棱锥
圆锥
球体
返回
2.下面几种图形:①三角形;②长方形;③正方体;
④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( ).
A.③⑤⑥ B.①②③ C.②③⑥ D.④⑤
A
3.如图所示,今年发射神十一的火箭.请写出图中含有的两种
立体图形: 、 .
圆锥 圆柱体
【课堂训练】
1.下列物体的形状类似于球体的是( ).
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
C
欧拉(Euler,1707-1783),伟大的瑞士数学家及自然科学家。
欧拉出生于牧师家庭,自幼已受到父亲的教育。13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。欧拉的惊人成就并不是偶然的。他可以在任何不良的环境中工作。欧拉在28岁时,不幸一只眼睛失明,过了30年以后,他的另一只眼睛也失明了。在他双目失明以后也没有停止过数学研究。他以惊人的毅力和坚忍不拔的精神继续工作着,在他双目失明至逝世的十七年间,还口述著作了几本书和400篇左右的论文。
课堂拓展
共同点:
1
2
3
4
围成立体图形的每一个面都是平的。
我们把像这样的图形称为多面体。
概 念:
合作交流
问题1:数出下列四个多面体的顶点数V、面数F、棱数E并填表
1
2
3
4
图形编号
顶点数V
面数F
棱数E
1
2
3
4
规律:
V+F-E=2
4
6
4
8
6
12
6
8
12
9
8
15
(欧拉公式)
【课堂训练】
一个凸多面体有12条棱,6个顶点,则这个多面体是几面体?
解析:
根据欧拉公式V(顶点数)+F(面数)-E(棱数)=2可知:
6+F-12=2
得:F=8
返回
线动成面
面动成体
点动成线
拓展延伸
面与面相交得到___;线与线相交得到___.
线
点
.
.
.
如图,第二行的图形围绕红线旋转一周,便能形成
第一行的某个几何体,用线连一连.
【例题】
D
A
B
C
1.如右图所示,把一个长方形绕着给定的直线旋转一周后,可能形成的几何体是( ).
【跟踪训练】
D
A.
B.
C.
D.
2.(广州·中考)将如图所示的直角梯形绕直线l旋转一
周,得到的立体图形是( ).
返回
C
1.能正确识别柱体、椎体、球体……
2.认识伟大的数学家欧拉和他的欧拉公式。
3.理解点、线、面是构成几何图形的基本元素。
谈谈本节课你有哪些收获?
如果命运是块顽石,我就化为大锤,将它砸得粉碎!
——Euler(欧拉)
圆柱
棱柱
棱锥
圆锥
生活中的立体图形
构成
分类
柱体
锥体
球体
多面体
谢 谢
1.通过观察认识到我们周围的规则物体能找到与他们相似的立体图形;
2.能正确识别柱体、椎体、球体……;
3.认识伟大的数学家欧拉和他的欧拉公式。
4.正确理解点、线、面是构成几何图形的基本元素,正确
理解点、线、面的关系.
自 主 学 习
1
课 堂 研 讨
2
合 作 交 流
3
拓 展 延 伸
4
归 纳 小 结
5
生活中你会经常看见很多实物,由下列实物能想象出
你熟悉的几何体吗?
返回
简单的几何体
柱体
锥体
球体
圆柱
棱柱
圆锥
棱锥
议一议:
柱体有何特点?
锥体有何特点?
棱柱
圆柱
棱锥
圆锥
球体
返回
2.下面几种图形:①三角形;②长方形;③正方体;
④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( ).
A.③⑤⑥ B.①②③ C.②③⑥ D.④⑤
A
3.如图所示,今年发射神十一的火箭.请写出图中含有的两种
立体图形: 、 .
圆锥 圆柱体
【课堂训练】
1.下列物体的形状类似于球体的是( ).
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
C
欧拉(Euler,1707-1783),伟大的瑞士数学家及自然科学家。
欧拉出生于牧师家庭,自幼已受到父亲的教育。13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。欧拉的惊人成就并不是偶然的。他可以在任何不良的环境中工作。欧拉在28岁时,不幸一只眼睛失明,过了30年以后,他的另一只眼睛也失明了。在他双目失明以后也没有停止过数学研究。他以惊人的毅力和坚忍不拔的精神继续工作着,在他双目失明至逝世的十七年间,还口述著作了几本书和400篇左右的论文。
课堂拓展
共同点:
1
2
3
4
围成立体图形的每一个面都是平的。
我们把像这样的图形称为多面体。
概 念:
合作交流
问题1:数出下列四个多面体的顶点数V、面数F、棱数E并填表
1
2
3
4
图形编号
顶点数V
面数F
棱数E
1
2
3
4
规律:
V+F-E=2
4
6
4
8
6
12
6
8
12
9
8
15
(欧拉公式)
【课堂训练】
一个凸多面体有12条棱,6个顶点,则这个多面体是几面体?
解析:
根据欧拉公式V(顶点数)+F(面数)-E(棱数)=2可知:
6+F-12=2
得:F=8
返回
线动成面
面动成体
点动成线
拓展延伸
面与面相交得到___;线与线相交得到___.
线
点
.
.
.
如图,第二行的图形围绕红线旋转一周,便能形成
第一行的某个几何体,用线连一连.
【例题】
D
A
B
C
1.如右图所示,把一个长方形绕着给定的直线旋转一周后,可能形成的几何体是( ).
【跟踪训练】
D
A.
B.
C.
D.
2.(广州·中考)将如图所示的直角梯形绕直线l旋转一
周,得到的立体图形是( ).
返回
C
1.能正确识别柱体、椎体、球体……
2.认识伟大的数学家欧拉和他的欧拉公式。
3.理解点、线、面是构成几何图形的基本元素。
谈谈本节课你有哪些收获?
如果命运是块顽石,我就化为大锤,将它砸得粉碎!
——Euler(欧拉)
圆柱
棱柱
棱锥
圆锥
生活中的立体图形
构成
分类
柱体
锥体
球体
多面体
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
