华东师大版八年级上册 数学 课件 :13.2.4角边角(20张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件 :13.2.4角边角(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 08:11:25 | ||
图片预览


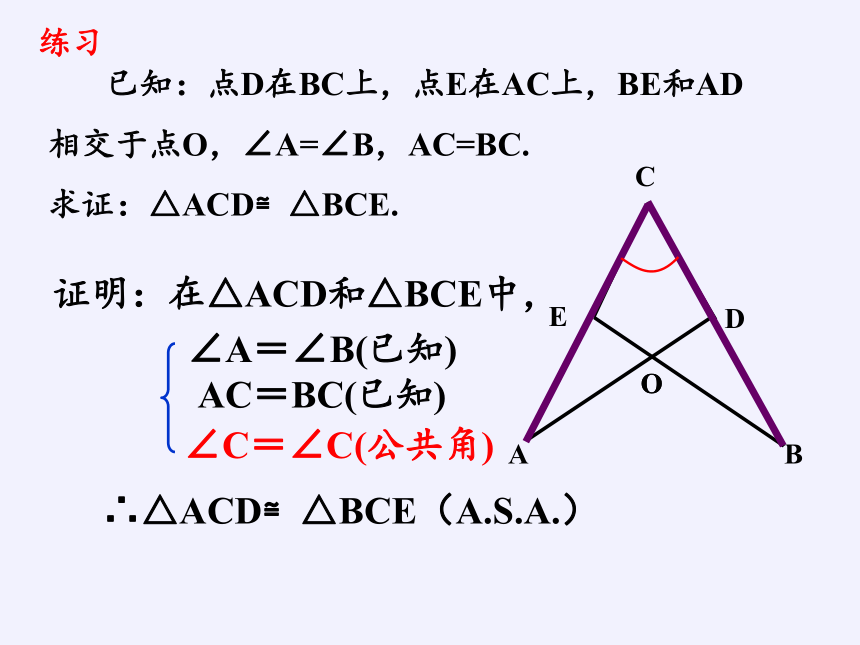
文档简介
角边角
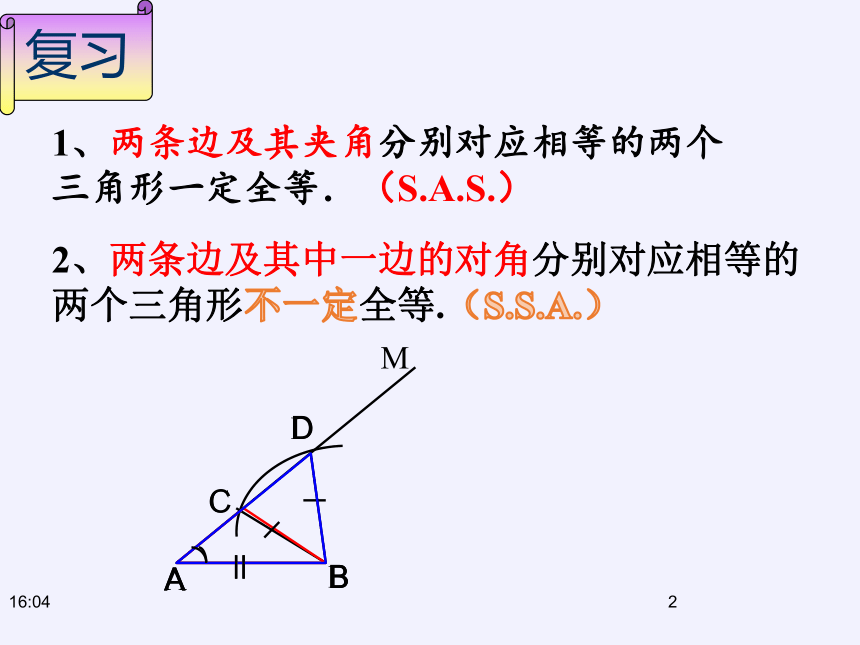
1、两条边及其夹角分别对应相等的两个三角形一定全等.(S.A.S.)
2、两条边及其中一边的对角分别对应相等的两个三角形不一定全等.(S.S.A.)
两角一边呢
A
B
M
C
D
A
B
C
A
B
D
复习
15:36
2
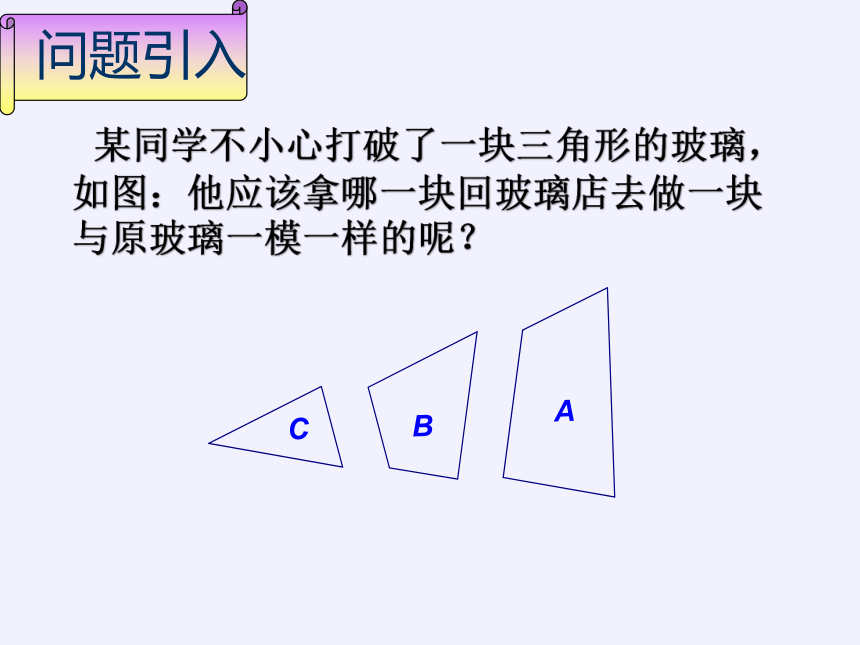
某同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店去做一块与原玻璃一模一样的呢?
问题引入
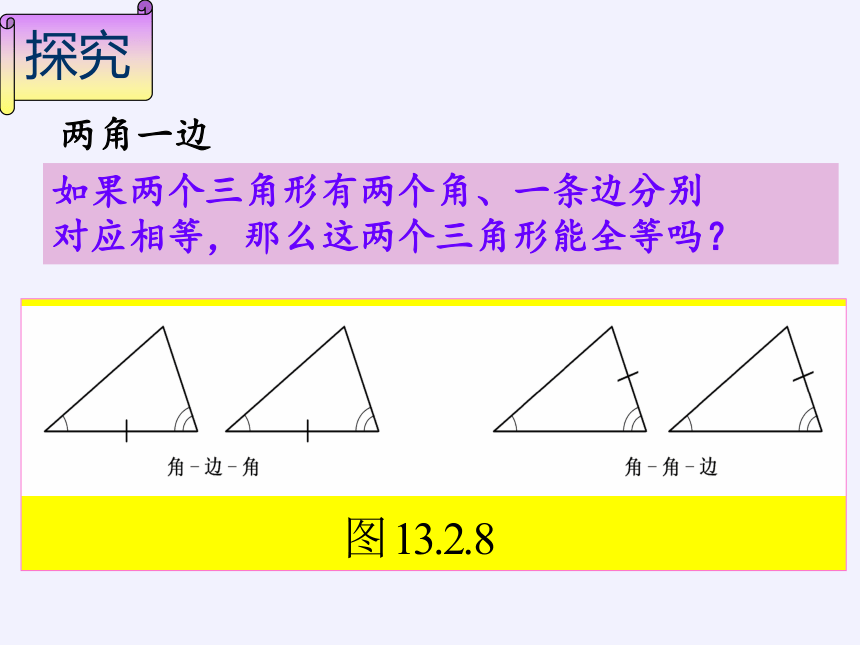
如果两个三角形有两个角、一条边分别
对应相等,那么这两个三角形能全等吗?
两角一边
探究
画法:
把你所画的三角形与其他同学所画的三角形比较,可以发现什么事实?
画一画
学生活动:按照下面的步骤画一个三角形,使它的两个内角分别为60°和 40°,并且这两个角夹边的边长为4cm。
(1)画一条线段AB,使AB=4cm;
(2)画∠MAB =60°,∠NBA= 40°,
MA与NB交与点C,△ABC即为所求。
全等
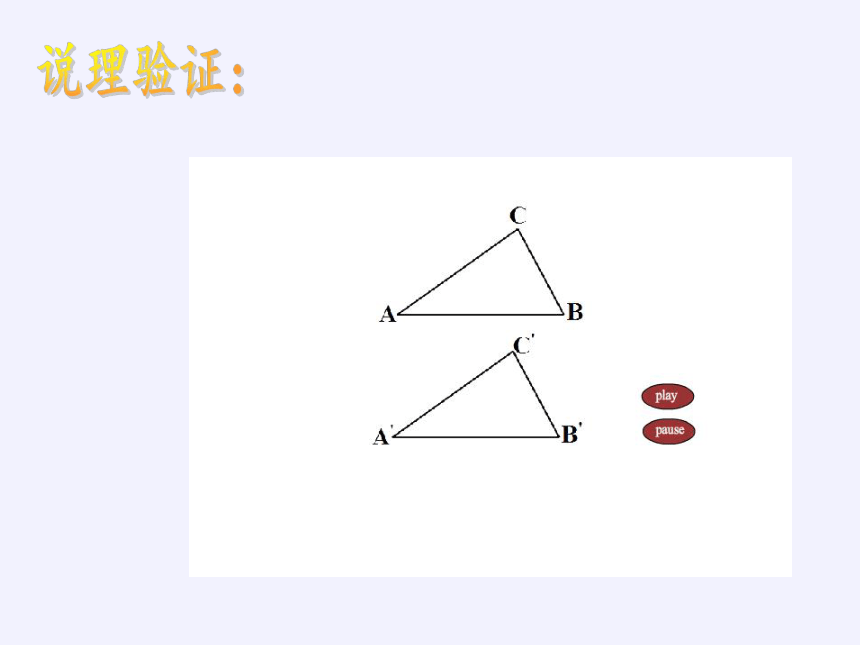
说理验证:
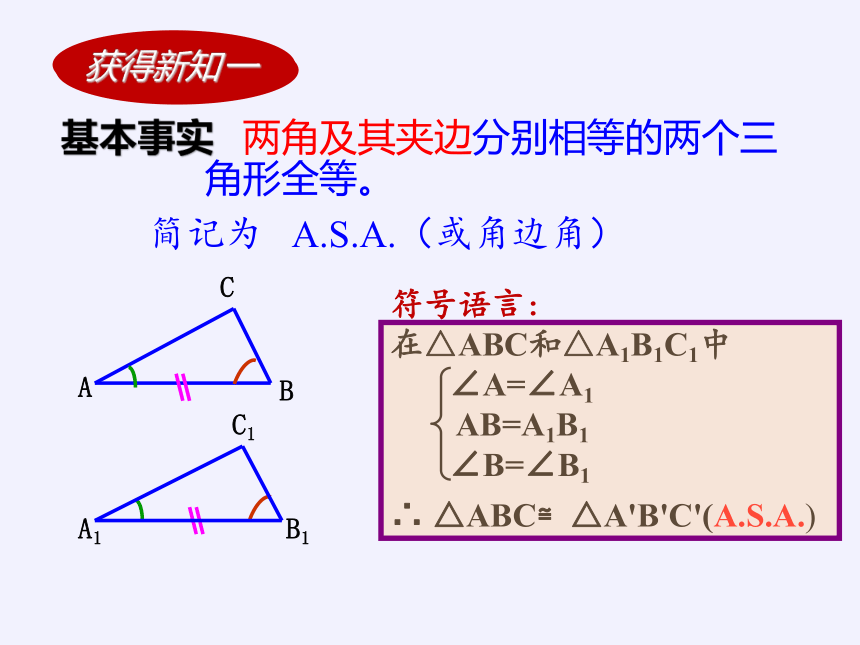
基本事实 两角及其夹边分别相等的两个三
角形全等。
简记为 A.S.A.(或角边角)
符号语言:
在△ABC和△A1B1C1中
∠A=∠A1
AB=A1B1
∠B=∠B1
∴ △ABC≌△A'B'C'(A.S.A.)
获得新知 一
C
A
B
A1
C1
B1
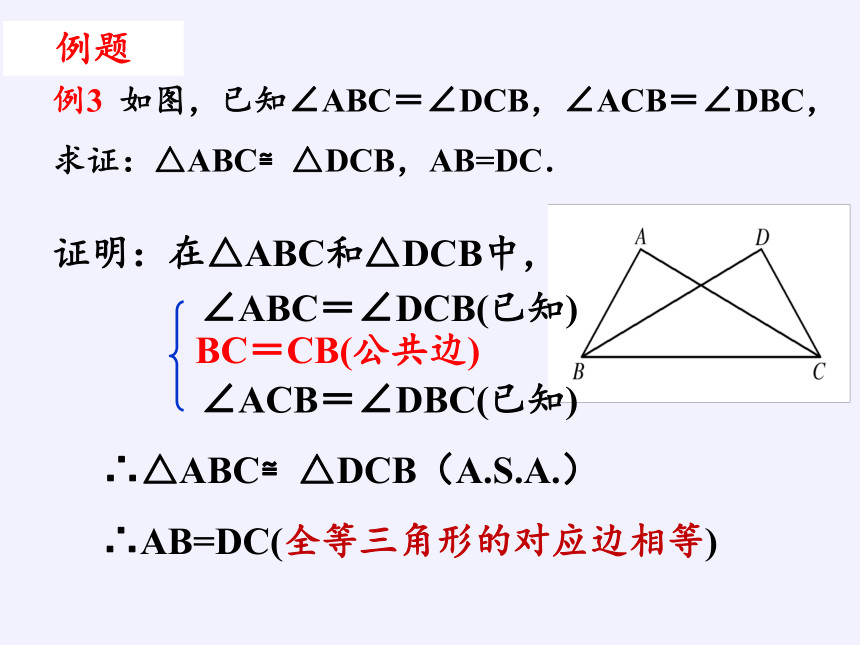
例3 如图,已知∠ABC=∠DCB,∠ACB=∠DBC,
求证:△ABC≌△DCB,AB=DC.
例题
证明:在△ABC和△DCB中,
∴△ABC≌△DCB(A.S.A.)
∠ABC=∠DCB(已知)
∠ACB=∠DBC(已知)
BC=CB(公共边)
∴AB=DC(全等三角形的对应边相等)
已知:点D在BC上,点E在AC上,BE和AD相交于点O,∠A=∠B,AC=BC.
求证:△ACD≌△BCE.
C
B
E
A
D
O
O
练习
证明:在△ACD和△BCE中,
∴△ACD≌△BCE(A.S.A.)
∠A=∠B(已知)
AC=BC(已知)
∠C=∠C(公共角)
思考: 如图,已知∠A=∠A1,∠B=∠B1,那么∠C=∠C1吗?为什么?
∵ ∠A=∠A1,∠B=∠B1
∴∠A+∠B+∠C1=180°
∠A1+∠B1+∠C1=180°
又∵∠A+∠B+∠C=180°
∴∠ C=∠C1
分析
思考: 如图,已知∠A=∠A1,∠B=∠B1,BC=B1C1,那么△ABC≌△A1B1C1吗?为什么?
∵ ∠A=∠A1,∠B=∠B1
∴∠A+∠B+∠C1=180°
∠A1+∠B1+∠C1=180°
又∵∠A+∠B+∠C=180°
∴∠ C=∠C1
解
在△ABC和△A1B1C1中
∠B=∠B1
BC=B1C1
∠C=∠C1
∴△ABC≌△A1B1(A.S.A.)
你能从中得到什么结论?
两角分别相等且一组等角的对边相等的两个三角形全等
两角分别相等且其中一组等角的对边相等的两个
三角形全等。
简记为 A.A.S.(或角角边)
判定定理:
∴ △ABC≌△A1B1C1(A.A.S.)
符号语言:
在△ABC和△A1B1C1中
∠A=∠A1
∠B=∠B1
BC=B1C1
获得新知二
判定三角形全等的方法:
判定方法一:S.A.S.(边角边)
判定方法二:A.S.A.(角边角)
判定方法三:A.A.S.(角角边)
1.如图,∠1=∠2.
(1)当BC=BD时,则△ABC≌△ABD的依据是 ;
(2)当∠3=∠4时,则△ABC≌△ABD的依据是 ;
(3)当∠C=∠D时,则△ABC≌△ABD的依据是 ;
三、巩固练习
边角边
角边角
角角边
A
B
C
D
E
图2
2. 如图2,已知线段AC、BD相交于点E,
AE=DE,∠A=∠D.求证△ABE≌△DCE.
证明:
在△ABE与△DCE中,
∠A=∠D (已知)
AE=DE (已知)
∠AEB=∠DEC (对顶角相等)
∴ △ABE≌△DCE(A.S.A.)
问题引入
某同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店做一块与原玻璃一模一样的呢?
谈谈本节课的收获
小结
P76习题13.2 第 4、5题
课后作业
练习 1、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,也不是哪组内角的对边,所以不全等。
谢 谢
1、两条边及其夹角分别对应相等的两个三角形一定全等.(S.A.S.)
2、两条边及其中一边的对角分别对应相等的两个三角形不一定全等.(S.S.A.)
两角一边呢
A
B
M
C
D
A
B
C
A
B
D
复习
15:36
2
某同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店去做一块与原玻璃一模一样的呢?
问题引入
如果两个三角形有两个角、一条边分别
对应相等,那么这两个三角形能全等吗?
两角一边
探究
画法:
把你所画的三角形与其他同学所画的三角形比较,可以发现什么事实?
画一画
学生活动:按照下面的步骤画一个三角形,使它的两个内角分别为60°和 40°,并且这两个角夹边的边长为4cm。
(1)画一条线段AB,使AB=4cm;
(2)画∠MAB =60°,∠NBA= 40°,
MA与NB交与点C,△ABC即为所求。
全等
说理验证:
基本事实 两角及其夹边分别相等的两个三
角形全等。
简记为 A.S.A.(或角边角)
符号语言:
在△ABC和△A1B1C1中
∠A=∠A1
AB=A1B1
∠B=∠B1
∴ △ABC≌△A'B'C'(A.S.A.)
获得新知 一
C
A
B
A1
C1
B1
例3 如图,已知∠ABC=∠DCB,∠ACB=∠DBC,
求证:△ABC≌△DCB,AB=DC.
例题
证明:在△ABC和△DCB中,
∴△ABC≌△DCB(A.S.A.)
∠ABC=∠DCB(已知)
∠ACB=∠DBC(已知)
BC=CB(公共边)
∴AB=DC(全等三角形的对应边相等)
已知:点D在BC上,点E在AC上,BE和AD相交于点O,∠A=∠B,AC=BC.
求证:△ACD≌△BCE.
C
B
E
A
D
O
O
练习
证明:在△ACD和△BCE中,
∴△ACD≌△BCE(A.S.A.)
∠A=∠B(已知)
AC=BC(已知)
∠C=∠C(公共角)
思考: 如图,已知∠A=∠A1,∠B=∠B1,那么∠C=∠C1吗?为什么?
∵ ∠A=∠A1,∠B=∠B1
∴∠A+∠B+∠C1=180°
∠A1+∠B1+∠C1=180°
又∵∠A+∠B+∠C=180°
∴∠ C=∠C1
分析
思考: 如图,已知∠A=∠A1,∠B=∠B1,BC=B1C1,那么△ABC≌△A1B1C1吗?为什么?
∵ ∠A=∠A1,∠B=∠B1
∴∠A+∠B+∠C1=180°
∠A1+∠B1+∠C1=180°
又∵∠A+∠B+∠C=180°
∴∠ C=∠C1
解
在△ABC和△A1B1C1中
∠B=∠B1
BC=B1C1
∠C=∠C1
∴△ABC≌△A1B1(A.S.A.)
你能从中得到什么结论?
两角分别相等且一组等角的对边相等的两个三角形全等
两角分别相等且其中一组等角的对边相等的两个
三角形全等。
简记为 A.A.S.(或角角边)
判定定理:
∴ △ABC≌△A1B1C1(A.A.S.)
符号语言:
在△ABC和△A1B1C1中
∠A=∠A1
∠B=∠B1
BC=B1C1
获得新知二
判定三角形全等的方法:
判定方法一:S.A.S.(边角边)
判定方法二:A.S.A.(角边角)
判定方法三:A.A.S.(角角边)
1.如图,∠1=∠2.
(1)当BC=BD时,则△ABC≌△ABD的依据是 ;
(2)当∠3=∠4时,则△ABC≌△ABD的依据是 ;
(3)当∠C=∠D时,则△ABC≌△ABD的依据是 ;
三、巩固练习
边角边
角边角
角角边
A
B
C
D
E
图2
2. 如图2,已知线段AC、BD相交于点E,
AE=DE,∠A=∠D.求证△ABE≌△DCE.
证明:
在△ABE与△DCE中,
∠A=∠D (已知)
AE=DE (已知)
∠AEB=∠DEC (对顶角相等)
∴ △ABE≌△DCE(A.S.A.)
问题引入
某同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店做一块与原玻璃一模一样的呢?
谈谈本节课的收获
小结
P76习题13.2 第 4、5题
课后作业
练习 1、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,也不是哪组内角的对边,所以不全等。
谢 谢
