华东师大版八年级上册 数学 课件: 13.2.5边边边(13张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件: 13.2.5边边边(13张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 680.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览





文档简介
边边边
1、什么是全等三角形?
2、我们已学过了哪几种三角形全等的判定方法?
知识回顾
能够完全重合的两个三角形是全等三角形
3种. 分别是S.A.S. A.S.A. A.A.S.
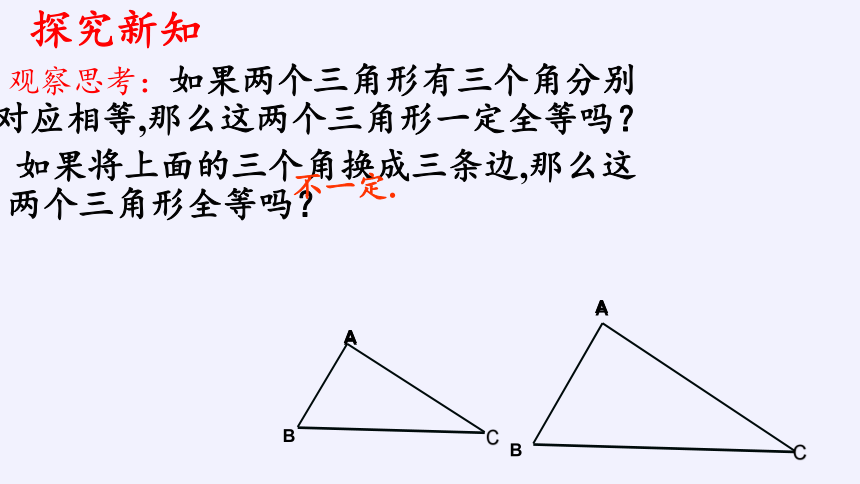
观察思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
如果将上面的三个角换成三条边,那么这两个三角形全等吗?
不一定.
探究新知
A
B
C
A
A
A
B
C
A
A
如图,已知三条线段,以这三条线段为边,画一个三角形.
动手操作
全等三角形的判定(sss)
基本事实: 三边分别相等的两个三角形全等简记为S.S.S. (或边边边)
几何语言:
A
B
C
D
E
F
在△ABC和△DEF中
∴ △ABC≌△DEF (S.S.S.)
例 已知:如图,在四边形ABCD中,AB = CD , AD = CB。 求证: ∠A = ∠C
新知运用
A
B
D
C
连结BD后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
证明:连结BD,
在△ABD和△CDB中,
∵AB =CD AD =CB(已知)
BD=DB(公共边),
∴ △ABD≌△CDB(S.S.S.)
∴ ∠A = ∠C(全等三角
形的对应角相等)
巩固提升
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△DCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?
全等(SAS)
全等(SSS)
不能判定全等
B
A
E
C
D
解:全等.理由如下:
∵ AE=BE CE=DE
∴AE+ DE=BE+CE
即AD=BC
在△ABC和△BAD中
∵AC=BD (已知)
BC=AD(已证)
AB=BA(公共边)
∴△ABC≌△BAD(S.S.S.)
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?
对应相等的元素
两边一角
两角一边
三角
三边
两边及其夹角
两边及其中一边的对角
两角及其夹边
两角及其中一角的对边
三角形是否全等
一定
(S.A.S)
不一定
一定
(A.S.A)
一定
(A.A.S)
不一定
一定
(S.S.S)
归纳:两个三角形全等的判定方法
判定三角形全等至少有一组边
这节课你有什么收获?
1、请说出目前判定三角形全等的4种方法:
S.A.S. A.S.A. A.A.S. S.S.S.
2、“边边边”在应用中用到的数学方法:
证明线段(或角)相等转化为证明线段(或角)所在的两个三角形全等
感谢各位老师莅临指导!
摄制单位: 祁东县教育局
导播合成: 周斐 陈胜利
摄制时间: 2018年 5月
谢 谢
1、什么是全等三角形?
2、我们已学过了哪几种三角形全等的判定方法?
知识回顾
能够完全重合的两个三角形是全等三角形
3种. 分别是S.A.S. A.S.A. A.A.S.
观察思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
如果将上面的三个角换成三条边,那么这两个三角形全等吗?
不一定.
探究新知
A
B
C
A
A
A
B
C
A
A
如图,已知三条线段,以这三条线段为边,画一个三角形.
动手操作
全等三角形的判定(sss)
基本事实: 三边分别相等的两个三角形全等简记为S.S.S. (或边边边)
几何语言:
A
B
C
D
E
F
在△ABC和△DEF中
∴ △ABC≌△DEF (S.S.S.)
例 已知:如图,在四边形ABCD中,AB = CD , AD = CB。 求证: ∠A = ∠C
新知运用
A
B
D
C
连结BD后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
证明:连结BD,
在△ABD和△CDB中,
∵AB =CD AD =CB(已知)
BD=DB(公共边),
∴ △ABD≌△CDB(S.S.S.)
∴ ∠A = ∠C(全等三角
形的对应角相等)
巩固提升
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△DCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?
全等(SAS)
全等(SSS)
不能判定全等
B
A
E
C
D
解:全等.理由如下:
∵ AE=BE CE=DE
∴AE+ DE=BE+CE
即AD=BC
在△ABC和△BAD中
∵AC=BD (已知)
BC=AD(已证)
AB=BA(公共边)
∴△ABC≌△BAD(S.S.S.)
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?
对应相等的元素
两边一角
两角一边
三角
三边
两边及其夹角
两边及其中一边的对角
两角及其夹边
两角及其中一角的对边
三角形是否全等
一定
(S.A.S)
不一定
一定
(A.S.A)
一定
(A.A.S)
不一定
一定
(S.S.S)
归纳:两个三角形全等的判定方法
判定三角形全等至少有一组边
这节课你有什么收获?
1、请说出目前判定三角形全等的4种方法:
S.A.S. A.S.A. A.A.S. S.S.S.
2、“边边边”在应用中用到的数学方法:
证明线段(或角)相等转化为证明线段(或角)所在的两个三角形全等
感谢各位老师莅临指导!
摄制单位: 祁东县教育局
导播合成: 周斐 陈胜利
摄制时间: 2018年 5月
谢 谢
