华东师大版八年级上册 数学 课件: 13.3.1等腰三角形的性质(15张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件: 13.3.1等腰三角形的性质(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 08:15:34 | ||
图片预览




文档简介
等腰三角形的性质
13.3 等腰三角形的性质
基本概念
A
在△ABC中,AB=AC,则这个三角形是等腰三角形。
相等的两边AB和AC叫腰,另一边BC叫底边。
两腰所夹的角∠A叫做顶角,一腰与底边所夹的角∠B和∠C叫做底角。
腰
腰
底角
顶角
底角
底边
B
C
D
操作与思考
1、请用纸剪一个两边相等的三角形。
3、将等腰三角形ABC沿着顶角平分线AD翻折,
你有怎样的发现?
2、再用量角器画出等腰三角形顶角的平分线AD。
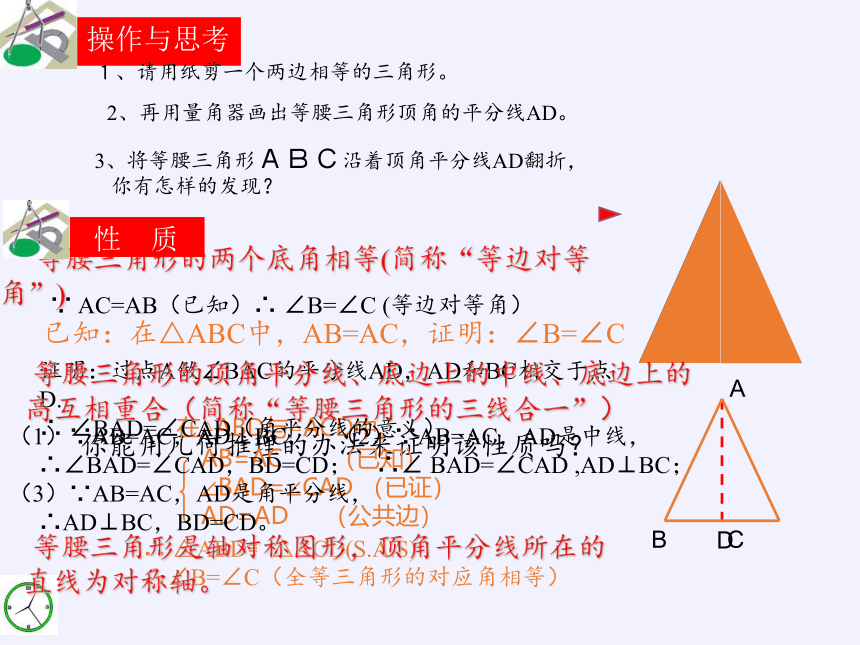
等腰三角形的两个底角相等(简称“等边对等角”)
性 质
你能用几何推理的办法来证明该性质吗?
已知:在△ABC中,AB=AC,证明:∠B=∠C
在△ABD与△ACD中,
AB=AC (已知)
∠BAD=∠CAD (已证)
AD=AD (公共边)
∴ △ABD≌△ACD(S.A.S)
∴∠B=∠C(全等三角形的对应角相等)
A
B C
证明:过点A做∠BAC的平分线AD,AD和BC相交于点D.
∴ ∠BAD=∠CAD(角平分线的意义)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
等腰三角形是轴对称图形,顶角平分线所在的直线为对称轴。
∵ AC=AB(已知)∴ ∠B=∠C (等边对等角)
(1)∵AB=AC,AD⊥BC, (2)∵AB=AC,AD是中线,
∴∠BAD=∠CAD,BD=CD; ∴∠ BAD=∠CAD ,AD⊥BC;
(3)∵AB=AC,AD是角平分线,
∴AD⊥BC,BD=CD。
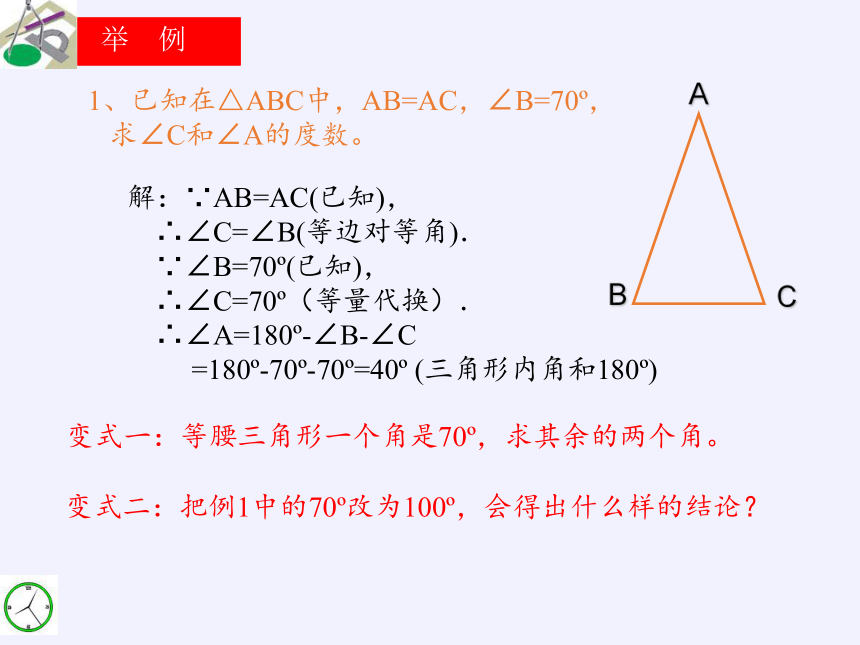
举 例
1、已知在△ABC中,AB=AC,∠B=70?,
求∠C和∠A的度数。
A
B
C
解:∵AB=AC(已知),
∴∠C=∠B(等边对等角).
∵∠B=70?(已知),
∴∠C=70?(等量代换).
∴∠A=180?-∠B-∠C
=180?-70?-70?=40? (三角形内角和180?)
变式一:等腰三角形一个角是70?,求其余的两个角。
变式二:把例1中的70?改为100?,会得出什么样的结论?
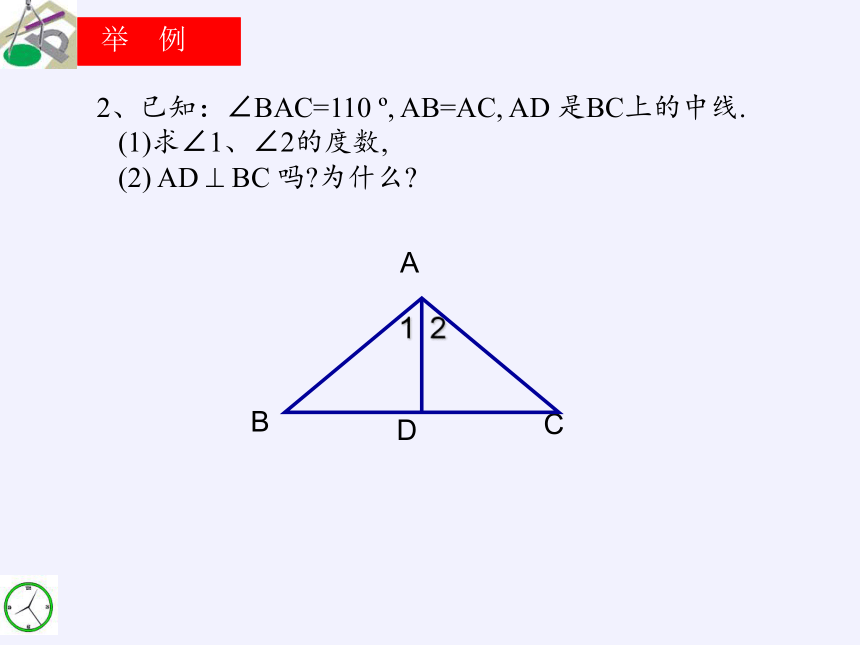
举 例
2、已知:∠BAC=110 ?, AB=AC, AD 是BC上的中线.
(1)求∠1、∠2的度数,
(2) AD ? BC 吗?为什么?
A
B
D
C
1
2
判断下列语句是否正确。
(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°.
( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )
×
×
作业
练 习
填空:
(1)在△ABC中,AB=AC,外角∠ACD=100,
则∠B= 度
(2)如图,在等腰三角形ABC中,AB=AC,D为BC的中点,
则点D到AB,AC的距离相等.请说明理由.
练 习
A
B
C
E
F
D
练 习
练 习
已知:如图,点D在AC上,点E在AB上,AB=AC,BC=BD,
AD=DE=BE,求∠A 的度数.
练 习
E
C
A
B
D
已知:AB=AD,BC=DC。
求证: 1、 ∠ABC=∠ADC
2、AC⊥BD
A
B
C
D
O
练 习
小 结
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角)
∵AB=AC
∴∠B=∠C
等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
A
B
C
A
C
B
D
1
2
作 业
导学:13.3 第一学时
谢 谢
13.3 等腰三角形的性质
基本概念
A
在△ABC中,AB=AC,则这个三角形是等腰三角形。
相等的两边AB和AC叫腰,另一边BC叫底边。
两腰所夹的角∠A叫做顶角,一腰与底边所夹的角∠B和∠C叫做底角。
腰
腰
底角
顶角
底角
底边
B
C
D
操作与思考
1、请用纸剪一个两边相等的三角形。
3、将等腰三角形ABC沿着顶角平分线AD翻折,
你有怎样的发现?
2、再用量角器画出等腰三角形顶角的平分线AD。
等腰三角形的两个底角相等(简称“等边对等角”)
性 质
你能用几何推理的办法来证明该性质吗?
已知:在△ABC中,AB=AC,证明:∠B=∠C
在△ABD与△ACD中,
AB=AC (已知)
∠BAD=∠CAD (已证)
AD=AD (公共边)
∴ △ABD≌△ACD(S.A.S)
∴∠B=∠C(全等三角形的对应角相等)
A
B C
证明:过点A做∠BAC的平分线AD,AD和BC相交于点D.
∴ ∠BAD=∠CAD(角平分线的意义)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
等腰三角形是轴对称图形,顶角平分线所在的直线为对称轴。
∵ AC=AB(已知)∴ ∠B=∠C (等边对等角)
(1)∵AB=AC,AD⊥BC, (2)∵AB=AC,AD是中线,
∴∠BAD=∠CAD,BD=CD; ∴∠ BAD=∠CAD ,AD⊥BC;
(3)∵AB=AC,AD是角平分线,
∴AD⊥BC,BD=CD。
举 例
1、已知在△ABC中,AB=AC,∠B=70?,
求∠C和∠A的度数。
A
B
C
解:∵AB=AC(已知),
∴∠C=∠B(等边对等角).
∵∠B=70?(已知),
∴∠C=70?(等量代换).
∴∠A=180?-∠B-∠C
=180?-70?-70?=40? (三角形内角和180?)
变式一:等腰三角形一个角是70?,求其余的两个角。
变式二:把例1中的70?改为100?,会得出什么样的结论?
举 例
2、已知:∠BAC=110 ?, AB=AC, AD 是BC上的中线.
(1)求∠1、∠2的度数,
(2) AD ? BC 吗?为什么?
A
B
D
C
1
2
判断下列语句是否正确。
(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°.
( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )
×
×
作业
练 习
填空:
(1)在△ABC中,AB=AC,外角∠ACD=100,
则∠B= 度
(2)如图,在等腰三角形ABC中,AB=AC,D为BC的中点,
则点D到AB,AC的距离相等.请说明理由.
练 习
A
B
C
E
F
D
练 习
练 习
已知:如图,点D在AC上,点E在AB上,AB=AC,BC=BD,
AD=DE=BE,求∠A 的度数.
练 习
E
C
A
B
D
已知:AB=AD,BC=DC。
求证: 1、 ∠ABC=∠ADC
2、AC⊥BD
A
B
C
D
O
练 习
小 结
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角)
∵AB=AC
∴∠B=∠C
等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
A
B
C
A
C
B
D
1
2
作 业
导学:13.3 第一学时
谢 谢
