华东师大版八年级上册 数学 13.2.6斜边直角边课件(共15张PPT)
文档属性
| 名称 | 华东师大版八年级上册 数学 13.2.6斜边直角边课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 346.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览




文档简介
斜边直角边
想一想
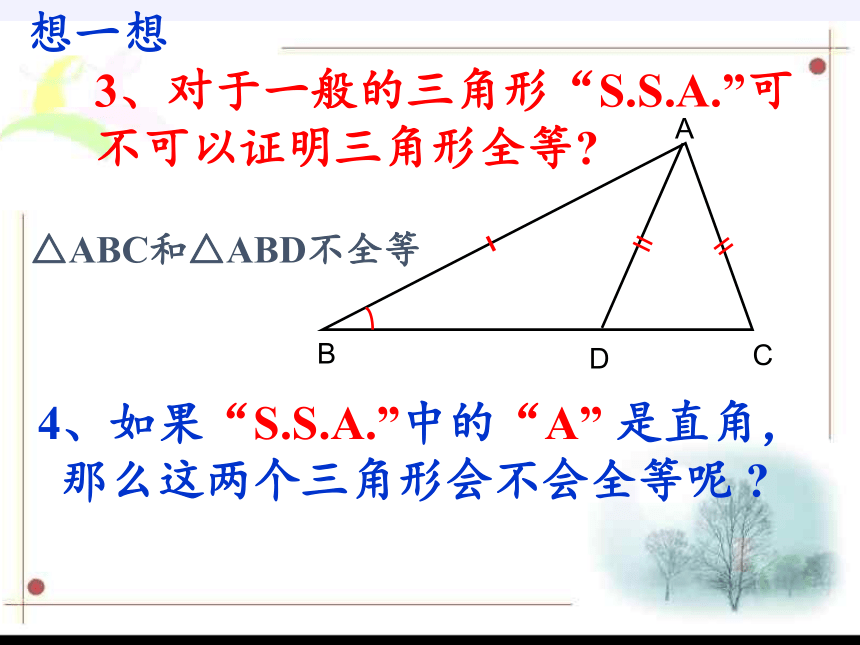
3、对于一般的三角形“S.S.A.”可不可以证明三角形全等?
4、如果“S.S.A.”中的“A” 是直角,
那么这两个三角形会不会全等呢 ?
A
B
C
D
△ABC和△ABD不全等
新课导学,预设问题
自主学习
1、已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一直角边,画一个直角三角形。
(1)你能试着画出来吗?与小组交流一下。
(2)把画好的Rt△ABC放到其他同学画的Rt△ABC上,它们全等吗?你能发现什么规律?
2、三种数学语言来表述“斜边直角边角基本事实”
3、你能够用几种方法说明两个直角三角形全等?
已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一直角边,画一个直角三角形。
(1)你能试着画出来吗?与小组交流一下。
步骤:
1、画一条线段AB,使它等于2cm;
2、画∠MAB=90°;
3、以B为圆心,以3cm为半径画弧,交射线AM于点C
4、连接BC。
△ABC就是所作三角形。
(2)把画好的Rt△ABC放到其他同学画的Rt△ABC上,它们全等吗?你能发现什么规律?
做一做:
条件一
条件二
前提条件
获得新知
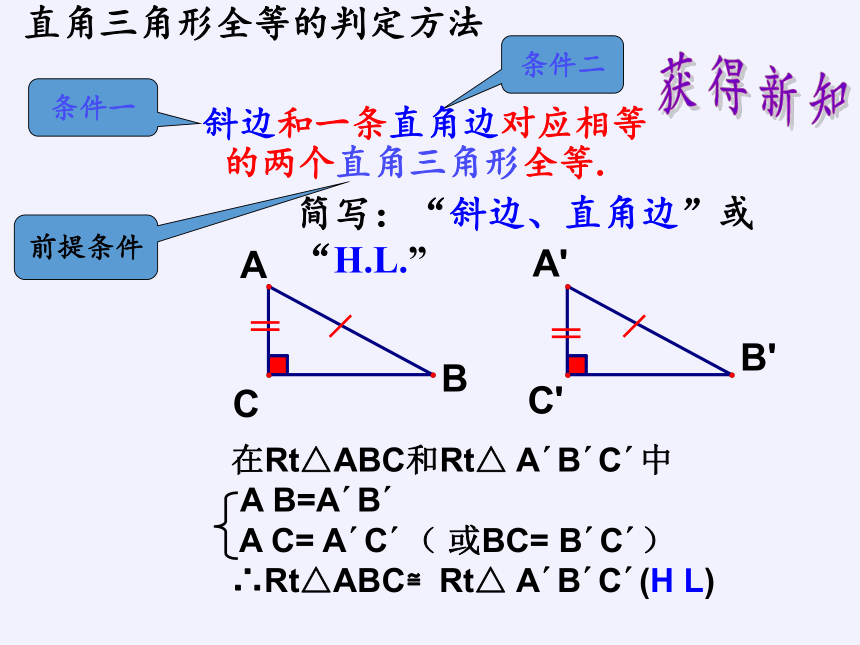
直角三角形全等的判定方法
斜边和一条直角边对应相等的两个直角三角形全等.
简写:“斜边、直角边”或“H.L.”
在Rt△ABC和Rt△ A?B?C?中
A B=A?B?
A C= A?C?( 或BC= B?C?)∴Rt△ABC≌Rt△ A?B?C?(H L)
想一想
你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”。
我们应根据具体问题的实际情况选择判断两个直角三角形全等的方法。
新课导学,预设问题
合作探究
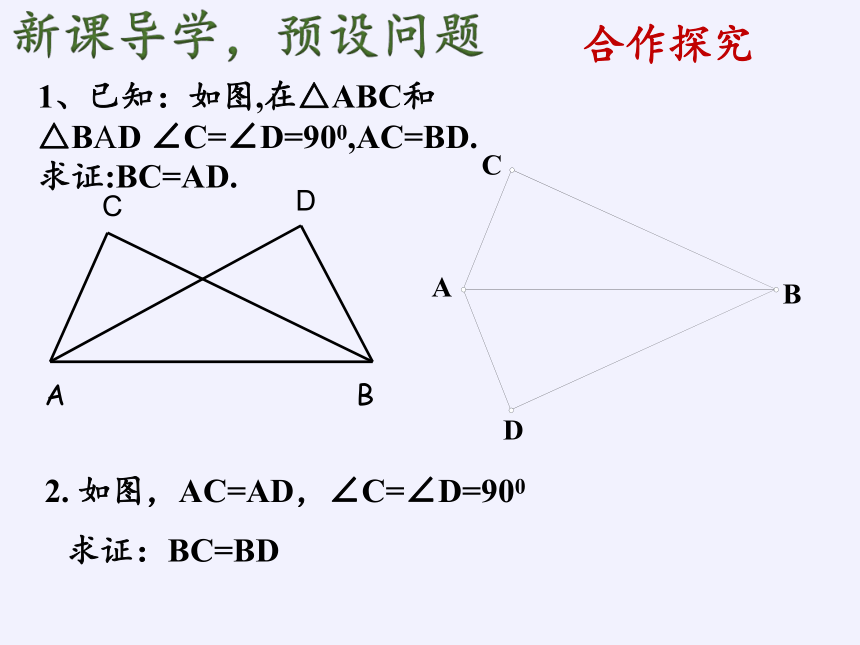
1、已知:如图,在△ABC和△BAD ∠C=∠D=900,AC=BD.
求证:BC=AD.
A
B
C
D
2. 如图,AC=AD,∠C=∠D=900
求证:BC=BD
A
B
C
D
已知:如图,在△ABC和△BAD 中∠C=∠D=900,AC=BD.
求证:BC=AD.
A
B
C
D
证明:∵ ∠C=∠D=900(已知)
∴ △ ABC和△ BAD都是直角三角形(直角三角形的定义)
在Rt △ ABC和Rt △ BAD中,
∵AC=BD,(已知)
AB=BA(公共边)
∴Rt △ ABC≌Rt △ BAD(H.L.)
∴ BC=AD(全等三角形的对应边相等)
学以致用
练一练
2. 如图,AC=AD,∠C=∠D=900,求证:BC=BD
C
D
A
B
解:在Rt△ACB和Rt△ADB中
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
1.如图,Rt△ABC,Rt△DEF中, ∠C=∠F=900要想证 Rt△ABC≌Rt△DEF ,
(1)添加条件________和_________,可用S.A.S.证明;
C
A
B
D
F
E
AC=DF
CB=FE
(4)添加条件________和_________,可用H.L.证明。
AB=DE
AC=DF
A.S.A.
(2)已知条件 ∠A=∠ D 和AC=DF ,可用 证明;
(3)添加条件∠A=∠ D和CB=FE
,可用 证明;
A.A.S.
看谁快!
达标小测
议一议
2、如图:有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
∠ABC+∠DFE=90°
解: ∠ABC+∠DFE=90°
在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
小结:这节课你有什么收获呢?与你的同伴进行交流
我们的生活离不开数学,我们要做生活的有心人。
再 见
谢 谢
想一想
3、对于一般的三角形“S.S.A.”可不可以证明三角形全等?
4、如果“S.S.A.”中的“A” 是直角,
那么这两个三角形会不会全等呢 ?
A
B
C
D
△ABC和△ABD不全等
新课导学,预设问题
自主学习
1、已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一直角边,画一个直角三角形。
(1)你能试着画出来吗?与小组交流一下。
(2)把画好的Rt△ABC放到其他同学画的Rt△ABC上,它们全等吗?你能发现什么规律?
2、三种数学语言来表述“斜边直角边角基本事实”
3、你能够用几种方法说明两个直角三角形全等?
已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一直角边,画一个直角三角形。
(1)你能试着画出来吗?与小组交流一下。
步骤:
1、画一条线段AB,使它等于2cm;
2、画∠MAB=90°;
3、以B为圆心,以3cm为半径画弧,交射线AM于点C
4、连接BC。
△ABC就是所作三角形。
(2)把画好的Rt△ABC放到其他同学画的Rt△ABC上,它们全等吗?你能发现什么规律?
做一做:
条件一
条件二
前提条件
获得新知
直角三角形全等的判定方法
斜边和一条直角边对应相等的两个直角三角形全等.
简写:“斜边、直角边”或“H.L.”
在Rt△ABC和Rt△ A?B?C?中
A B=A?B?
A C= A?C?( 或BC= B?C?)∴Rt△ABC≌Rt△ A?B?C?(H L)
想一想
你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”。
我们应根据具体问题的实际情况选择判断两个直角三角形全等的方法。
新课导学,预设问题
合作探究
1、已知:如图,在△ABC和△BAD ∠C=∠D=900,AC=BD.
求证:BC=AD.
A
B
C
D
2. 如图,AC=AD,∠C=∠D=900
求证:BC=BD
A
B
C
D
已知:如图,在△ABC和△BAD 中∠C=∠D=900,AC=BD.
求证:BC=AD.
A
B
C
D
证明:∵ ∠C=∠D=900(已知)
∴ △ ABC和△ BAD都是直角三角形(直角三角形的定义)
在Rt △ ABC和Rt △ BAD中,
∵AC=BD,(已知)
AB=BA(公共边)
∴Rt △ ABC≌Rt △ BAD(H.L.)
∴ BC=AD(全等三角形的对应边相等)
学以致用
练一练
2. 如图,AC=AD,∠C=∠D=900,求证:BC=BD
C
D
A
B
解:在Rt△ACB和Rt△ADB中
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
1.如图,Rt△ABC,Rt△DEF中, ∠C=∠F=900要想证 Rt△ABC≌Rt△DEF ,
(1)添加条件________和_________,可用S.A.S.证明;
C
A
B
D
F
E
AC=DF
CB=FE
(4)添加条件________和_________,可用H.L.证明。
AB=DE
AC=DF
A.S.A.
(2)已知条件 ∠A=∠ D 和AC=DF ,可用 证明;
(3)添加条件∠A=∠ D和CB=FE
,可用 证明;
A.A.S.
看谁快!
达标小测
议一议
2、如图:有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
∠ABC+∠DFE=90°
解: ∠ABC+∠DFE=90°
在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
小结:这节课你有什么收获呢?与你的同伴进行交流
我们的生活离不开数学,我们要做生活的有心人。
再 见
谢 谢
