华东师大版八年级上册 数学 13.5.2线段垂直平分线课件(共23张PPT)
文档属性
| 名称 | 华东师大版八年级上册 数学 13.5.2线段垂直平分线课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 267.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览







文档简介
线段垂直平分线
学习目标 :
1.能说出线段垂直平分线的性质定理及其逆定理的概念。
2.能熟练应用线段的性质定理及其逆定理进行证明和计算,并能解决实际问题。
农安县政府经济局为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
情境引入
问题:
线段是轴对称图形吗?它的对称轴是什么?
情境引入
A
M
N
P
C
B
问题:
画出线段AB的垂直平分线MN,在MN上任取一点P,连接AP和BP,再将图形MN对折,你有什么发现?
合作探究:互动1
线段垂直平分线上的点到这条线段两个端点的距离相等.
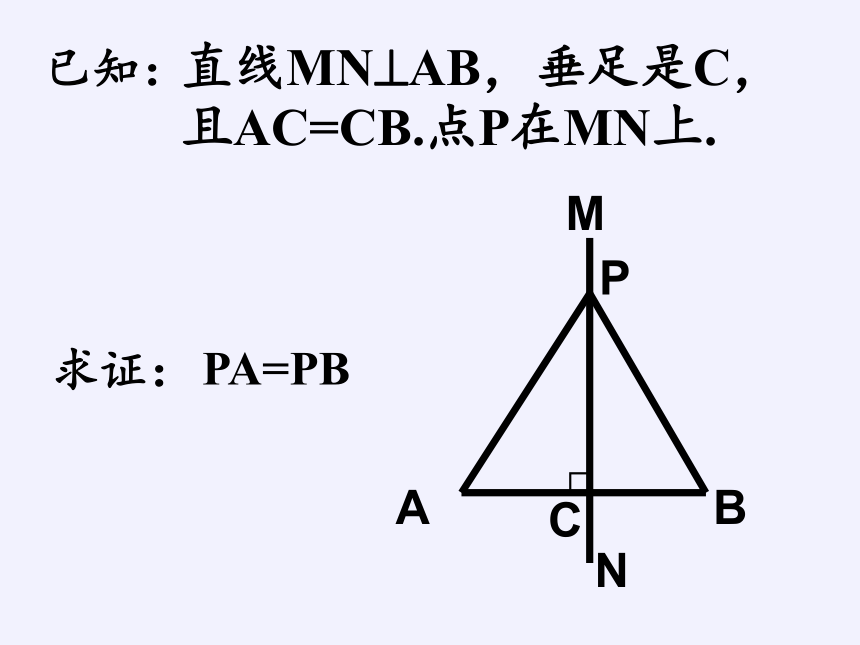
直线MN?AB,垂足是C,且AC=CB.点P在MN上.
已知:
PA=PB
求证:
A
B
C
N
M
P
?
证明:
∵MN?AB(已知)
∴?PCA=?PCB(垂直的定义)
在?PCA和?PCB中,
AC=BC(已知),
?PCA=?PCB(已证)
PC=PC(公共边)
∴ ?PCA ≌ ?PCB(SAS)
∴PA=PB(全等三角形的对应边相等)
A
B
C
N
M
P
?
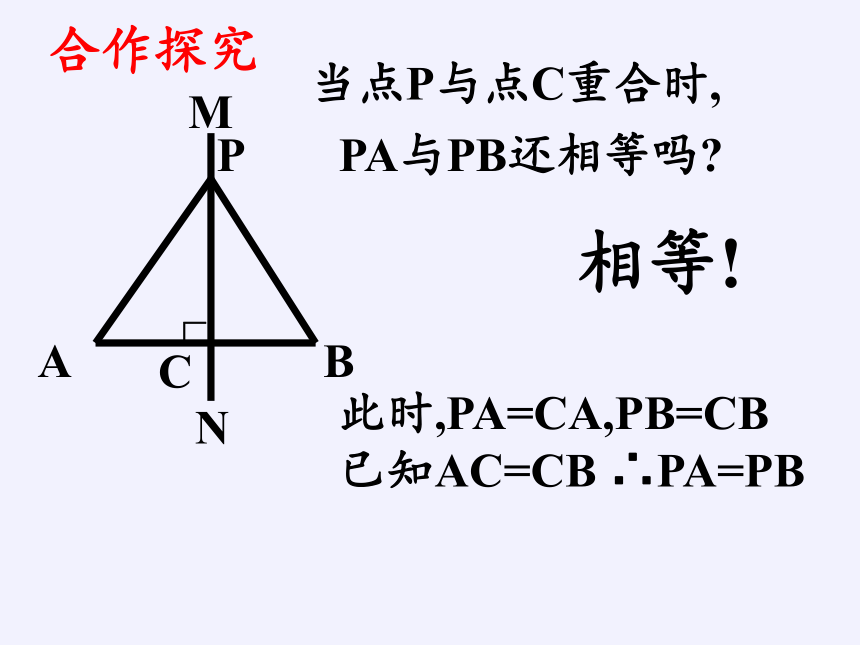
当点P与点C重合时,
PA与PB还相等吗?
相等!
此时,PA=CA,PB=CB
已知AC=CB ∴PA=PB
合作探究
A
B
C
N
M
P
?
结论:
线段的垂直平分线上的点,到这条线段两个端点的距离相等.
线段垂直平分线的性质定理
∵直线MN?AB,且AC=CB.点P在MN上
∴PA=PB(线段的垂直平分线上的点,和这条线段两个端点的距离相等)
推理格式:
定理可以用来证明两条线段相等
(或三角形是等腰三角形).
1.已知:如图,AB=AC,?A=30o,AB的垂直平分线MN交AC于D,则? 1= , ? 2= .
A
B
C
D
M
N
30o
1
2
75o
30o
60o
45o
2.已知:如图,AB=AC,AB的垂直平分线MN交AC于D,如果AC=5cm,BC=4cm,则△CDB .
A
B
C
D
M
N
9cm
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
问题:
这个定理的逆命题是什么?
合作探究-互动2
A
B
Q
C
?
已知:
如图QA=QB
求证:
点Q在线段AB的垂直
平分线上.
过点Q作QC?AB垂足为C.
∵ QA=QB(已知)
∴ ?QAB是等腰三角形(等腰三角 形的定义)
∴AC=BC(等腰三角形底边上的高是底边上的中线)
∴QC是线段AB的垂直平分线.
即点Q在线段AB的垂直平分线MN上.
证明:
∵ ?QAB是等腰三角形,且QC?AB
结论:
逆定理可以用来证明点在直线上(或直线经过某一点).
逆定理:线段垂直平分线的判定定理
∵QA=QB
∴点Q在线段AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
推理格式:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
例 已知:如图?ABC中,边AB、BC的垂直平分线相交于点P.
求证:点P在边AC的垂直平分线上.
A
C
B
M
P
N
M/
N/
一个三角形的三条边的垂直平分线交于一点,这个点到三角形三个顶点的距离相等.
结论:
练习:
已知:ΔABC中,D在BC上,BD+AD=BC
求证:点D在AC的垂直平分线上
C
D
B
A
·
A
B
C
生活中的数学
农安县政府经济局为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,
才能使得它到三个小区的距
离相等。
国道102号线高 速 公 路
A
B
在国道102号线L(农安段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,县政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
生活中的数学
L
P
1、线段垂直平分线上的点到这条线段两个端点的距离相等.
2、到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
3、一个三角形的三条边的垂直平分线交于一点,这个点到三角形三个顶点的距离相等.
小结:
布置作业:
1.基础作业:教材课后练习题。
2.导学作业:
在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?
A
O
B
. C
. D
谢 谢
学习目标 :
1.能说出线段垂直平分线的性质定理及其逆定理的概念。
2.能熟练应用线段的性质定理及其逆定理进行证明和计算,并能解决实际问题。
农安县政府经济局为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
情境引入
问题:
线段是轴对称图形吗?它的对称轴是什么?
情境引入
A
M
N
P
C
B
问题:
画出线段AB的垂直平分线MN,在MN上任取一点P,连接AP和BP,再将图形MN对折,你有什么发现?
合作探究:互动1
线段垂直平分线上的点到这条线段两个端点的距离相等.
直线MN?AB,垂足是C,且AC=CB.点P在MN上.
已知:
PA=PB
求证:
A
B
C
N
M
P
?
证明:
∵MN?AB(已知)
∴?PCA=?PCB(垂直的定义)
在?PCA和?PCB中,
AC=BC(已知),
?PCA=?PCB(已证)
PC=PC(公共边)
∴ ?PCA ≌ ?PCB(SAS)
∴PA=PB(全等三角形的对应边相等)
A
B
C
N
M
P
?
当点P与点C重合时,
PA与PB还相等吗?
相等!
此时,PA=CA,PB=CB
已知AC=CB ∴PA=PB
合作探究
A
B
C
N
M
P
?
结论:
线段的垂直平分线上的点,到这条线段两个端点的距离相等.
线段垂直平分线的性质定理
∵直线MN?AB,且AC=CB.点P在MN上
∴PA=PB(线段的垂直平分线上的点,和这条线段两个端点的距离相等)
推理格式:
定理可以用来证明两条线段相等
(或三角形是等腰三角形).
1.已知:如图,AB=AC,?A=30o,AB的垂直平分线MN交AC于D,则? 1= , ? 2= .
A
B
C
D
M
N
30o
1
2
75o
30o
60o
45o
2.已知:如图,AB=AC,AB的垂直平分线MN交AC于D,如果AC=5cm,BC=4cm,则△CDB .
A
B
C
D
M
N
9cm
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
问题:
这个定理的逆命题是什么?
合作探究-互动2
A
B
Q
C
?
已知:
如图QA=QB
求证:
点Q在线段AB的垂直
平分线上.
过点Q作QC?AB垂足为C.
∵ QA=QB(已知)
∴ ?QAB是等腰三角形(等腰三角 形的定义)
∴AC=BC(等腰三角形底边上的高是底边上的中线)
∴QC是线段AB的垂直平分线.
即点Q在线段AB的垂直平分线MN上.
证明:
∵ ?QAB是等腰三角形,且QC?AB
结论:
逆定理可以用来证明点在直线上(或直线经过某一点).
逆定理:线段垂直平分线的判定定理
∵QA=QB
∴点Q在线段AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
推理格式:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
例 已知:如图?ABC中,边AB、BC的垂直平分线相交于点P.
求证:点P在边AC的垂直平分线上.
A
C
B
M
P
N
M/
N/
一个三角形的三条边的垂直平分线交于一点,这个点到三角形三个顶点的距离相等.
结论:
练习:
已知:ΔABC中,D在BC上,BD+AD=BC
求证:点D在AC的垂直平分线上
C
D
B
A
·
A
B
C
生活中的数学
农安县政府经济局为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,
才能使得它到三个小区的距
离相等。
国道102号线高 速 公 路
A
B
在国道102号线L(农安段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,县政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
生活中的数学
L
P
1、线段垂直平分线上的点到这条线段两个端点的距离相等.
2、到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
3、一个三角形的三条边的垂直平分线交于一点,这个点到三角形三个顶点的距离相等.
小结:
布置作业:
1.基础作业:教材课后练习题。
2.导学作业:
在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?
A
O
B
. C
. D
谢 谢
