华东师大版八年级上册 数学 课件: 13.5.3角平分线(21张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件: 13.5.3角平分线(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 170.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 10:41:15 | ||
图片预览








文档简介
角平分线
一、教学背景的分析
1.教学内容分析
本节课是在七年级学习了角平分线的概念和前面刚学完证明三角形全等的基础上进行教学的.内容包括角平分线的性质及初步应用. 角平分线的性质是全等三角形知识的延续,为证明线段或角相等开辟了新的途径,同时也为后面角平分线的判定定理的学习奠定了基础.因此,本节内容在数学知识体系中起到了承上启下的作用.
2.教学对象分析
刚进入初二的学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强引导.
一、教学背景的分析
重点:理解角的平分线的性质并能初步
运用.
难点:(1)对定理中 点 到角两边的
距离的正确理解;
(2)对于性质定理的运用
一、教学背景的分析
3.教学重点、难点
1.知识与技能
理解角的平分线的性质并能初步运用.
2.数学思考
通过让学生经历观察,猜想,验证,应用等过程,培养学生用数学知识解决问题的能力.
二、教学目标
1.教学方法
本节课我坚持“教与学、知识与能力的辩证统一”和“使每个学生都得到充分发展”的原则,采用引导发现法、主动探究法、讲授教学法,指导学生“动手操作,合作交流,自主探究”.鼓励学生多思、多说、多练,努力做到教法、学法的最优组合.
三、教学方法
A
O
B
E
D
C
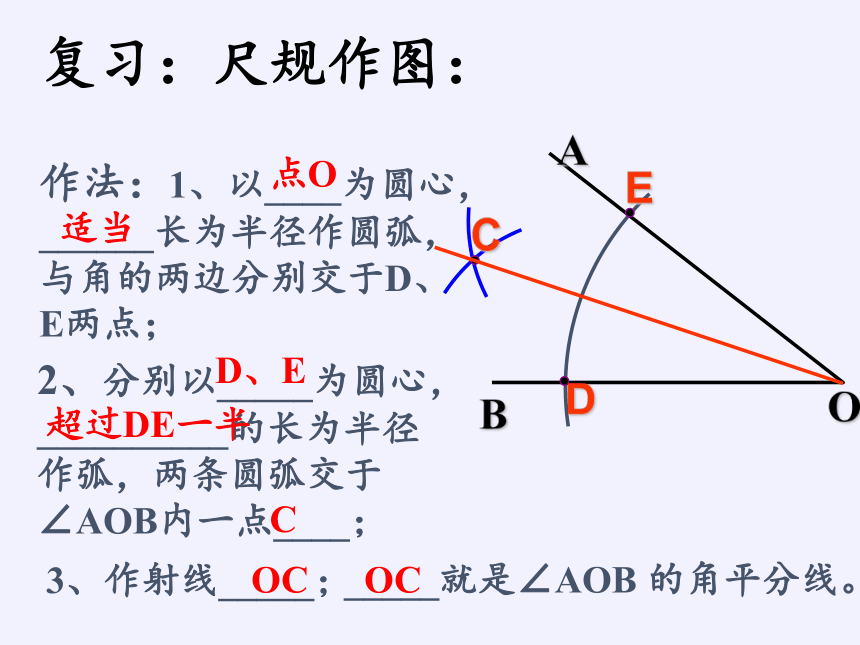
复习:尺规作图:
作法:1、以____为圆心,
______长为半径作圆弧,
与角的两边分别交于D、
E两点;
2、分别以_____为圆心,
__________的长为半径
作弧,两条圆弧交于
∠AOB内一点____;
3、作射线_____;
_____就是∠AOB 的角平分线。
点O
适当
D、E
超过DE一半
C
OC
OC
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
角平分线上的点到角两边的距离相等。
D
P
E
A
O
B
C
角平分线的性质定理
角的平分线上的点到角两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵ ∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴ PD=PE
(角平分线上的点到角两边的距离相等)
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角平分线上的点到角两边的距离相等。
BD CD
(×)
判断:
练习1
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角平分线上的点到角两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
角平分线上的点到角两边的距离相等。
√
不必再证全等
如图,△ABC中, AD是∠BAC的平分线, ∠C=90°,DE⊥AB于E,BC=8,BD=5,求DE.
A
C
D
B
E
例1
在△OAB中,OE是它的角平分线,且EA=EB,EC、ED分别垂直OA,OB,垂足为C,D.求证:AC=BD.
O
A
B
E
C
D
例2
练习2
1、在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BD=7,DE=3.求BC的长
E
D
C
B
A
2 . 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。
60
BF
3.已知△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
4、 如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB
A
C
D
E
B
F
◆这节课我们学习了哪些知识?
小 结
已知:在等腰Rt△ABC中,AC = BC
∠C=90°,AD平分∠ BAC,DE⊥AB于点E。
求证:BD+DE =AC
E
C
D
B
A
巩固提高
谢 谢
一、教学背景的分析
1.教学内容分析
本节课是在七年级学习了角平分线的概念和前面刚学完证明三角形全等的基础上进行教学的.内容包括角平分线的性质及初步应用. 角平分线的性质是全等三角形知识的延续,为证明线段或角相等开辟了新的途径,同时也为后面角平分线的判定定理的学习奠定了基础.因此,本节内容在数学知识体系中起到了承上启下的作用.
2.教学对象分析
刚进入初二的学生观察、操作、猜想能力较强,但归纳、运用数学意识的思想比较薄弱,思维的广阔性、敏捷性、灵活性比较欠缺,需要在课堂教学中进一步加强引导.
一、教学背景的分析
重点:理解角的平分线的性质并能初步
运用.
难点:(1)对定理中 点 到角两边的
距离的正确理解;
(2)对于性质定理的运用
一、教学背景的分析
3.教学重点、难点
1.知识与技能
理解角的平分线的性质并能初步运用.
2.数学思考
通过让学生经历观察,猜想,验证,应用等过程,培养学生用数学知识解决问题的能力.
二、教学目标
1.教学方法
本节课我坚持“教与学、知识与能力的辩证统一”和“使每个学生都得到充分发展”的原则,采用引导发现法、主动探究法、讲授教学法,指导学生“动手操作,合作交流,自主探究”.鼓励学生多思、多说、多练,努力做到教法、学法的最优组合.
三、教学方法
A
O
B
E
D
C
复习:尺规作图:
作法:1、以____为圆心,
______长为半径作圆弧,
与角的两边分别交于D、
E两点;
2、分别以_____为圆心,
__________的长为半径
作弧,两条圆弧交于
∠AOB内一点____;
3、作射线_____;
_____就是∠AOB 的角平分线。
点O
适当
D、E
超过DE一半
C
OC
OC
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴ PD=PE(全等三角形的对应边相等)
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO(AAS)
角平分线上的点到角两边的距离相等。
D
P
E
A
O
B
C
角平分线的性质定理
角的平分线上的点到角两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵ ∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴ PD=PE
(角平分线上的点到角两边的距离相等)
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
角平分线上的点到角两边的距离相等。
BD CD
(×)
判断:
练习1
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角平分线上的点到角两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
角平分线上的点到角两边的距离相等。
√
不必再证全等
如图,△ABC中, AD是∠BAC的平分线, ∠C=90°,DE⊥AB于E,BC=8,BD=5,求DE.
A
C
D
B
E
例1
在△OAB中,OE是它的角平分线,且EA=EB,EC、ED分别垂直OA,OB,垂足为C,D.求证:AC=BD.
O
A
B
E
C
D
例2
练习2
1、在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BD=7,DE=3.求BC的长
E
D
C
B
A
2 . 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。
60
BF
3.已知△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
4、 如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB
A
C
D
E
B
F
◆这节课我们学习了哪些知识?
小 结
已知:在等腰Rt△ABC中,AC = BC
∠C=90°,AD平分∠ BAC,DE⊥AB于点E。
求证:BD+DE =AC
E
C
D
B
A
巩固提高
谢 谢
