华东师大版八年级上册 数学 课件 :13.5.3角平分线1(26张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件 :13.5.3角平分线1(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 08:43:09 | ||
图片预览







文档简介
八年级数学(上册)第13章
华东师范大学出版社
《义务教育教科书》
如图,两条小河交汇形成的三角区,土壤肥沃,气候宜人,小牛看中了这块宝地,想在这里建一个小房子,并使房子到两条小河的距离相等,但它不知该如何选址,你能帮帮它吗?
新课导入
请你帮帮它
房子该建在哪儿呢?
§13.5.3 角平分线
1.探索并掌握角平分线的性质定理和判定定理.
2.能灵活运用角平分线的性质定理和判定定理解决有关问题.
学习重难点:灵活运用角的平分线性质定理和判定定理定理解题
学习目标:(1分钟)
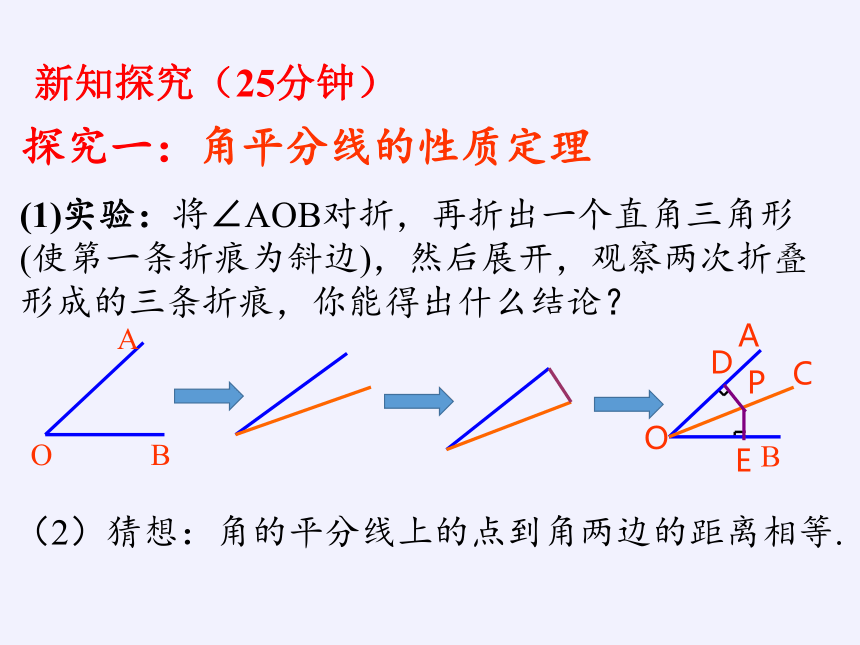
(2)猜想:角的平分线上的点到角两边的距离相等.
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
A
O
B
B
A
O
C
D
P
E
新知探究(25分钟)
探究一:角平分线的性质定理
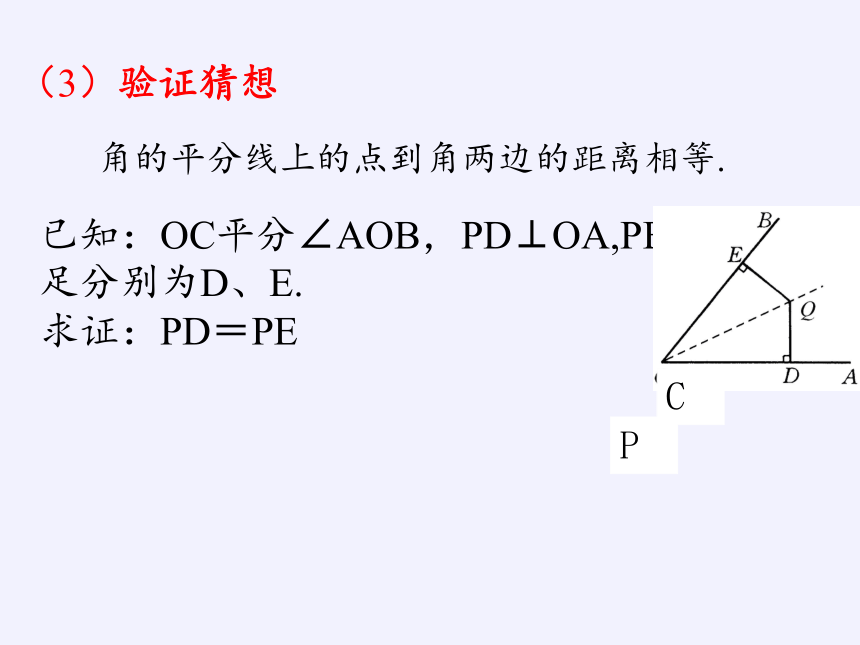
(3)验证猜想
已知:OC平分∠AOB,PD⊥OA,PE⊥OB垂足分别为D、E.
求证:PD=PE
角的平分线上的点到角两边的距离相等.
P
C
P
C
(4)归纳总结:
角平分线的性质定理:
角平分线上的点到角两边的距离相等。
用几何语言表示为:
∵ OP是∠AOB的平分线
PD⊥OA,PE⊥OB
∴ PD=PE
推理的理由有三个,必须写完全,不能少了任何一个。
B
思考:
如图所示,OC是∠AOB 的平分线,P 是OC上任意一点.则PE是否等于PD呢?为什么?
O
A
E
D
C
P
PD,PE没有垂直OA,OB,它们不是角平分线上任一点到这个角两边的距离,所以不一定相等.
例1、如图,D是∠AOB的平分线上一点,DC⊥OA,ED⊥OB,垂足分别为点C和点E,连接CE.
求证:∠DCE=∠DEC
A
典例剖析
1、如图,在△ABC中,AD=4,AB=3,AC平分∠BAD,则S△ABC:S△ACD= .
拓展提升
D
C
A
B
探究二:角平分线的判定定理
(1)角平分线的性质定理反过来会有什么样的结果呢?
这个命题是否正确?你能用逻辑推理的方法加以验证吗?试一试.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
条件
结论
性质定理
逆命题
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角平分线上的点
到角两边的距离相等
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}到角两边的距离相等的点
在角的平分线上
已知:如图,PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE.
(2)证明命题
到角两边距离相等的点在角的平分线上.
P
C
求证:点P在∠AOB的平分线上.
P
C
(3)得出结论:
角平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上.
用几何语言表示为:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P在∠AOB的平分线上.
推理的理由有三个,必须写完全,不能少了任何一个。
例2、已知:如图,BF⊥AC,CE⊥AB,BF与CE交于点D,且BE=CF.
求证:AD平分∠BAC.
F
A
E
D
B
C
典例剖析
如图,△ABC中∠ABC、∠ACB的角平分线交于点P,PF⊥AB,PG⊥AC,PE⊥BC.
(1)求证:PF=PG=PE.
(2)点P是否在∠BAC平分线上?
由此你能得出什么结论?
A
B
C
P
E
F
G
三角形的三条角平分线交与一点,且这一点到三角形三边的距离相等.
结论
如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
小试牛刀
(2015.上海)已知:如图,在Rt△ABC中∠A=90°,∠ABC 的平分线BD交AC于点D,AD=2, BC=10,则△BCD的面积为 .
A
B
D
C
体验中考
1、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4,则PE=______.
A
D
O
B
E
P
C
巩固练习,拓展提高(5分钟)
2、如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为 .
A
C
D
B
E
3.已知:如图,在梯形ABCD中,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:AM平分∠DAB.
D
M
C
B
A
N
课堂小结(2分钟)
1.角平分线的性质定理:
角平分线上的点到角两边的距离相等.
2.角平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上.
3.三角形的三条角平分线交于一点,且这一点到三角形三边的距离相等.
检测指导:
1、 闭卷检测,独立完成(4分钟)
2、 出示答案,对子互批(1分钟)
3、 自主纠错,反思错因(1分钟)
4、 组汇报,师生点拨(1分钟)
达标检测,当堂反馈(7分钟)
1、D
2、2
3、4:5:6
4、证明:
过点F分别作AE、BC、AD的垂线,P、M、N为垂足
∵CF是∠BCE的平分线,
∴FP=FM.
同理:FM=FN.
∴FP=FN.
∴点F在∠DAE的平分线上.
达标测试答案
P
M
N
强化补救
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是7,DE=2,AB=4,则AC的长是( )
A 4 B 3 C 6 D 5
作业
课本第99页 4、5题
谢 谢
华东师范大学出版社
《义务教育教科书》
如图,两条小河交汇形成的三角区,土壤肥沃,气候宜人,小牛看中了这块宝地,想在这里建一个小房子,并使房子到两条小河的距离相等,但它不知该如何选址,你能帮帮它吗?
新课导入
请你帮帮它
房子该建在哪儿呢?
§13.5.3 角平分线
1.探索并掌握角平分线的性质定理和判定定理.
2.能灵活运用角平分线的性质定理和判定定理解决有关问题.
学习重难点:灵活运用角的平分线性质定理和判定定理定理解题
学习目标:(1分钟)
(2)猜想:角的平分线上的点到角两边的距离相等.
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
A
O
B
B
A
O
C
D
P
E
新知探究(25分钟)
探究一:角平分线的性质定理
(3)验证猜想
已知:OC平分∠AOB,PD⊥OA,PE⊥OB垂足分别为D、E.
求证:PD=PE
角的平分线上的点到角两边的距离相等.
P
C
P
C
(4)归纳总结:
角平分线的性质定理:
角平分线上的点到角两边的距离相等。
用几何语言表示为:
∵ OP是∠AOB的平分线
PD⊥OA,PE⊥OB
∴ PD=PE
推理的理由有三个,必须写完全,不能少了任何一个。
B
思考:
如图所示,OC是∠AOB 的平分线,P 是OC上任意一点.则PE是否等于PD呢?为什么?
O
A
E
D
C
P
PD,PE没有垂直OA,OB,它们不是角平分线上任一点到这个角两边的距离,所以不一定相等.
例1、如图,D是∠AOB的平分线上一点,DC⊥OA,ED⊥OB,垂足分别为点C和点E,连接CE.
求证:∠DCE=∠DEC
A
典例剖析
1、如图,在△ABC中,AD=4,AB=3,AC平分∠BAD,则S△ABC:S△ACD= .
拓展提升
D
C
A
B
探究二:角平分线的判定定理
(1)角平分线的性质定理反过来会有什么样的结果呢?
这个命题是否正确?你能用逻辑推理的方法加以验证吗?试一试.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
条件
结论
性质定理
逆命题
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角平分线上的点
到角两边的距离相等
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}到角两边的距离相等的点
在角的平分线上
已知:如图,PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE.
(2)证明命题
到角两边距离相等的点在角的平分线上.
P
C
求证:点P在∠AOB的平分线上.
P
C
(3)得出结论:
角平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上.
用几何语言表示为:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P在∠AOB的平分线上.
推理的理由有三个,必须写完全,不能少了任何一个。
例2、已知:如图,BF⊥AC,CE⊥AB,BF与CE交于点D,且BE=CF.
求证:AD平分∠BAC.
F
A
E
D
B
C
典例剖析
如图,△ABC中∠ABC、∠ACB的角平分线交于点P,PF⊥AB,PG⊥AC,PE⊥BC.
(1)求证:PF=PG=PE.
(2)点P是否在∠BAC平分线上?
由此你能得出什么结论?
A
B
C
P
E
F
G
三角形的三条角平分线交与一点,且这一点到三角形三边的距离相等.
结论
如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
小试牛刀
(2015.上海)已知:如图,在Rt△ABC中∠A=90°,∠ABC 的平分线BD交AC于点D,AD=2, BC=10,则△BCD的面积为 .
A
B
D
C
体验中考
1、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4,则PE=______.
A
D
O
B
E
P
C
巩固练习,拓展提高(5分钟)
2、如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为 .
A
C
D
B
E
3.已知:如图,在梯形ABCD中,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:AM平分∠DAB.
D
M
C
B
A
N
课堂小结(2分钟)
1.角平分线的性质定理:
角平分线上的点到角两边的距离相等.
2.角平分线的判定定理:
角的内部到角两边距离相等的点在角的平分线上.
3.三角形的三条角平分线交于一点,且这一点到三角形三边的距离相等.
检测指导:
1、 闭卷检测,独立完成(4分钟)
2、 出示答案,对子互批(1分钟)
3、 自主纠错,反思错因(1分钟)
4、 组汇报,师生点拨(1分钟)
达标检测,当堂反馈(7分钟)
1、D
2、2
3、4:5:6
4、证明:
过点F分别作AE、BC、AD的垂线,P、M、N为垂足
∵CF是∠BCE的平分线,
∴FP=FM.
同理:FM=FN.
∴FP=FN.
∴点F在∠DAE的平分线上.
达标测试答案
P
M
N
强化补救
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是7,DE=2,AB=4,则AC的长是( )
A 4 B 3 C 6 D 5
作业
课本第99页 4、5题
谢 谢
