华东师大版八年级上册 数学 课件: 14.1.2直角三角形的判定(17张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件: 14.1.2直角三角形的判定(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 08:44:12 | ||
图片预览




文档简介
直角三角形的判定
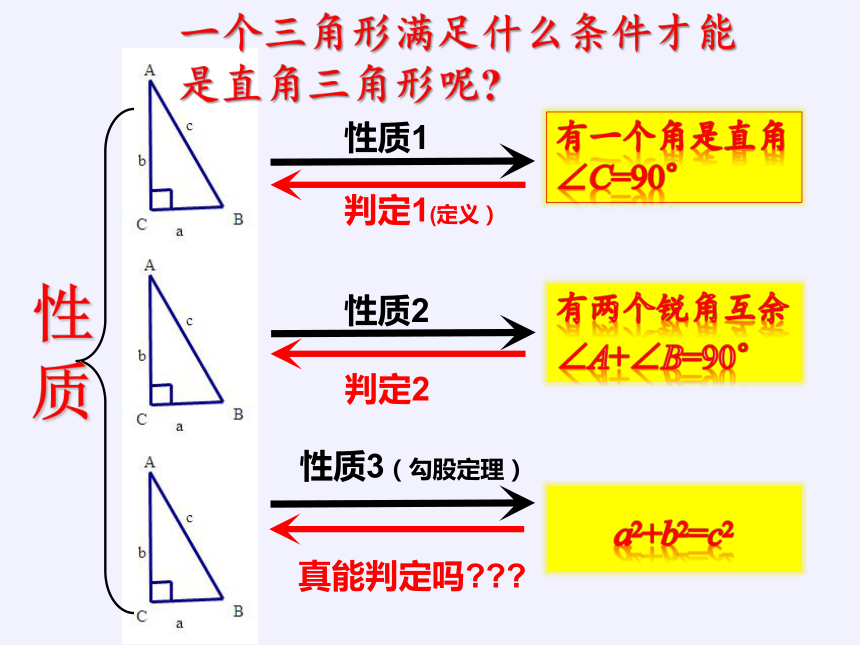
有一个角是直角∠C=90°
有两个锐角互余
∠A+∠B=90°
a2+b2=c2
性质
一个三角形满足什么条件才能是直角三角形呢?
性质1
判定1(定义)
性质2
判定2
性质3(勾股定理)
真能判定吗???
按照这种做法真能得到一个直角三角形吗?
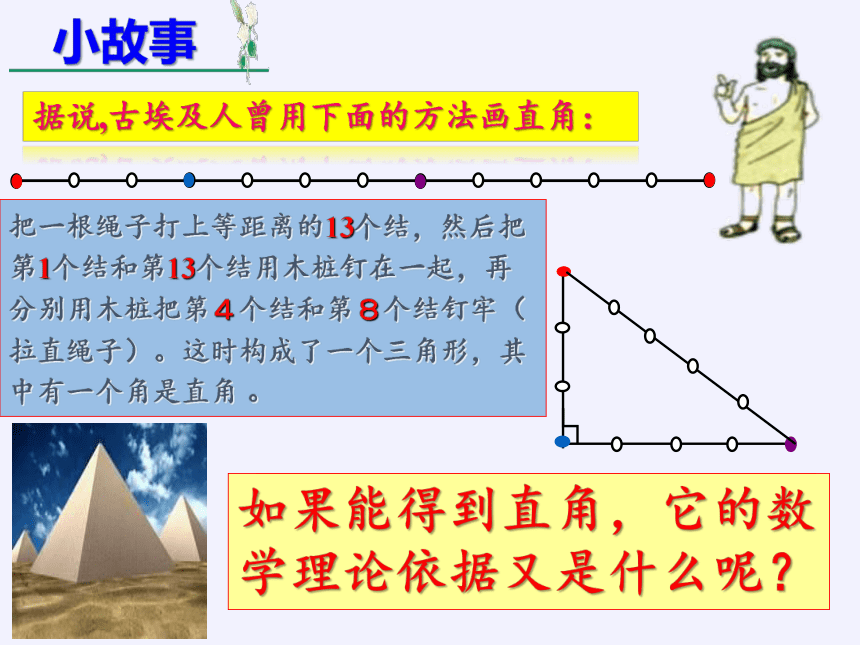
据说,古埃及人曾用下面的方法画直角:
小故事
把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。这时构成了一个三角形,其中有一个角是直角 。
如果能得到直角,它的数学理论依据又是什么呢?
合作探究
探讨三边长度分别为如下数据的三角形,猜想它们是些什么形状的三角形?(单位:cm 请按角分类)
请比较上述每个三角形的两条较短边的平方和与最长边的平方之间的大小关系.
直角三角形
52+122 = 132
画板
三角形的边满足什么条件才是直角三角形?
如果三角形的三边长a、b、c满足a2 + b2=c2
那么这个三角形是直角三角形。
直角三角形
62+82 = 102
52+62 > 72
锐角三角形
(3)5,6,7
(2)5,12,13
(1)6,8,10
命 题 : 如果三角形的三边长a、b、c满足a2 + b2=c2 ,那么这个三角形是直角三角形。
已知△ABC,AB=c,AC=b,BC=a,且a2+b2=c2
求证: ∠C=90 °
证明:作Rt△A′B′C′,
使∠C′=90°,A′C′=b,B′C′=a
∴△ABC≌ △A′B′C′(SSS)
∴∠C= ∠C′=90°
则
A
C
a
B
b
c
又∵ a2 + b2= c2
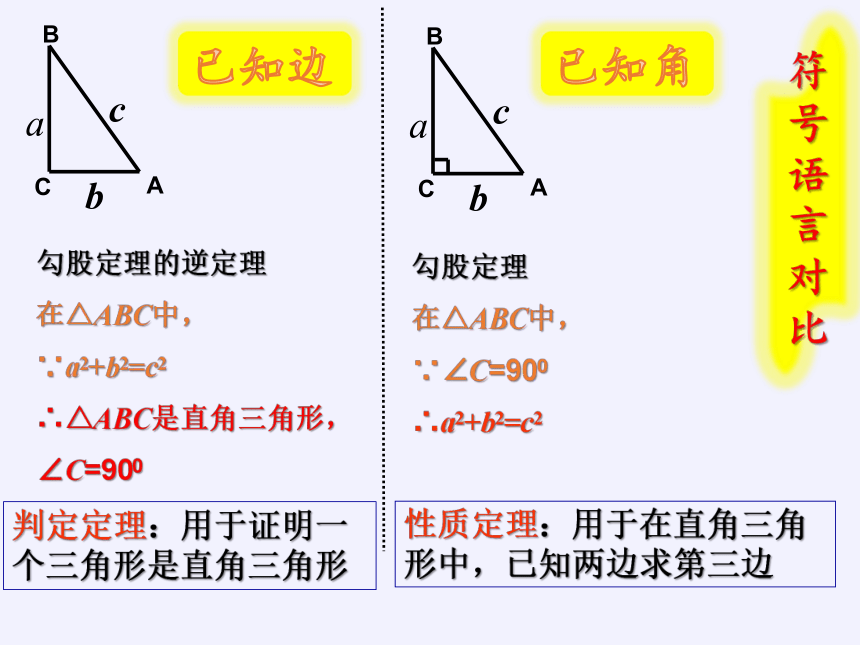
勾股定理的逆定理:
同一证法
文字语言对比
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
如果三角形的三边长 a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
勾股定理的逆定理:
(即一个三角形的两条较短边的平方和等于最长边的平方,那么这个三角形是直角三角形。)
勾股定理的逆定理
在△ABC中,
∵a2+b2=c2
∴△ABC是直角三角形,
∠C=900
勾股定理
在△ABC中,
∵∠C=900
∴a2+b2=c2
判定定理:用于证明一个三角形是直角三角形
性质定理:用于在直角三角形中,已知两边求第三边
a
c
b
B
C
A
a
c
b
B
C
A
符
号
语
言
对
比
已知角
已知边
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最大边长的平方.
例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=4,b=5,c=6
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为6
∵42+52=16+25=41
62 =36
∴42+ 52 ≠ 62
∴以4, 5, 6为边长的三角形不是直角三角形
方法:找、算、比、判
(3) a=1 b=2 c= ____ _____ ;
下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一条边所对的角是直角?
(1) a= b=2 c=1 ____ _____ ;
(2) a=3 b=4 c= 3 ____ _____ ;
yes
No
yes
边a
边b
小试牛刀
方法:找、算、比、判
(4) a=3 b=4 c= 6 ____ _____ ;
No
已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c, ,b=2n,
(n>1的正整数)
求证:△ABC是直角三角形
证明:
大展身手
∴△ABC是直角三角形
方法:找、算、比、判
当n=2时
a=3,b=4,c=5
当n=3时
a=8,b=6,c=10
当n=4时
a=15,b=8,c=17
………….
像3、4、5;6、8、10等能构成为直角三角形三条边长的三个正整数,称为勾股数
又∵
∵
例2 已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
A
B
C
D
3
4
12
13
5
∟
3
4
12
13
典例剖析
提示:勾股定理 勾股定理的逆定理
不规则图形求面积方法之一:分割
有一块田地的形状和尺寸如图所示∠ADC=90°,试求它的面积。
投影仪
巩固提高
A
B
C
3
4
13
12
D
不规则图形求面积方法之二:补全
课堂小结
通过本节课的学习,同学们掌握了哪些知识及其解题方法?
有一个角是直角∠C=90°
有两个锐角互余
∠A+∠B=90°
a2+b2=c2
性质
直角三角形的判定(角、边)
性质1
判定1(定义)
性质2
判定2
性质3(勾股定理)
判定3(勾股定理的逆定理)
判定
数学解题方法
勾股定理的逆定理运用方法:
找、算、比、判
不规则图形求面积方法:
分割、补全
课堂检测
1.(1)5,4,2;
(2)6,8,4;
(3)3a,4a,5a(a>0)
以上各组数能组成直角三角形的是__________(填序号).
2.如右图,网格图由边长为1的小正方形组成,求△ABC的面积。
谢 谢
有一个角是直角∠C=90°
有两个锐角互余
∠A+∠B=90°
a2+b2=c2
性质
一个三角形满足什么条件才能是直角三角形呢?
性质1
判定1(定义)
性质2
判定2
性质3(勾股定理)
真能判定吗???
按照这种做法真能得到一个直角三角形吗?
据说,古埃及人曾用下面的方法画直角:
小故事
把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。这时构成了一个三角形,其中有一个角是直角 。
如果能得到直角,它的数学理论依据又是什么呢?
合作探究
探讨三边长度分别为如下数据的三角形,猜想它们是些什么形状的三角形?(单位:cm 请按角分类)
请比较上述每个三角形的两条较短边的平方和与最长边的平方之间的大小关系.
直角三角形
52+122 = 132
画板
三角形的边满足什么条件才是直角三角形?
如果三角形的三边长a、b、c满足a2 + b2=c2
那么这个三角形是直角三角形。
直角三角形
62+82 = 102
52+62 > 72
锐角三角形
(3)5,6,7
(2)5,12,13
(1)6,8,10
命 题 : 如果三角形的三边长a、b、c满足a2 + b2=c2 ,那么这个三角形是直角三角形。
已知△ABC,AB=c,AC=b,BC=a,且a2+b2=c2
求证: ∠C=90 °
证明:作Rt△A′B′C′,
使∠C′=90°,A′C′=b,B′C′=a
∴△ABC≌ △A′B′C′(SSS)
∴∠C= ∠C′=90°
则
A
C
a
B
b
c
又∵ a2 + b2= c2
勾股定理的逆定理:
同一证法
文字语言对比
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
如果三角形的三边长 a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
勾股定理的逆定理:
(即一个三角形的两条较短边的平方和等于最长边的平方,那么这个三角形是直角三角形。)
勾股定理的逆定理
在△ABC中,
∵a2+b2=c2
∴△ABC是直角三角形,
∠C=900
勾股定理
在△ABC中,
∵∠C=900
∴a2+b2=c2
判定定理:用于证明一个三角形是直角三角形
性质定理:用于在直角三角形中,已知两边求第三边
a
c
b
B
C
A
a
c
b
B
C
A
符
号
语
言
对
比
已知角
已知边
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最大边长的平方.
例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=4,b=5,c=6
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为6
∵42+52=16+25=41
62 =36
∴42+ 52 ≠ 62
∴以4, 5, 6为边长的三角形不是直角三角形
方法:找、算、比、判
(3) a=1 b=2 c= ____ _____ ;
下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一条边所对的角是直角?
(1) a= b=2 c=1 ____ _____ ;
(2) a=3 b=4 c= 3 ____ _____ ;
yes
No
yes
边a
边b
小试牛刀
方法:找、算、比、判
(4) a=3 b=4 c= 6 ____ _____ ;
No
已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c, ,b=2n,
(n>1的正整数)
求证:△ABC是直角三角形
证明:
大展身手
∴△ABC是直角三角形
方法:找、算、比、判
当n=2时
a=3,b=4,c=5
当n=3时
a=8,b=6,c=10
当n=4时
a=15,b=8,c=17
………….
像3、4、5;6、8、10等能构成为直角三角形三条边长的三个正整数,称为勾股数
又∵
∵
例2 已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
A
B
C
D
3
4
12
13
5
∟
3
4
12
13
典例剖析
提示:勾股定理 勾股定理的逆定理
不规则图形求面积方法之一:分割
有一块田地的形状和尺寸如图所示∠ADC=90°,试求它的面积。
投影仪
巩固提高
A
B
C
3
4
13
12
D
不规则图形求面积方法之二:补全
课堂小结
通过本节课的学习,同学们掌握了哪些知识及其解题方法?
有一个角是直角∠C=90°
有两个锐角互余
∠A+∠B=90°
a2+b2=c2
性质
直角三角形的判定(角、边)
性质1
判定1(定义)
性质2
判定2
性质3(勾股定理)
判定3(勾股定理的逆定理)
判定
数学解题方法
勾股定理的逆定理运用方法:
找、算、比、判
不规则图形求面积方法:
分割、补全
课堂检测
1.(1)5,4,2;
(2)6,8,4;
(3)3a,4a,5a(a>0)
以上各组数能组成直角三角形的是__________(填序号).
2.如右图,网格图由边长为1的小正方形组成,求△ABC的面积。
谢 谢
