华东师大版八年级上册 数学 14.2 勾股定理的应用课件(共24张PPT)
文档属性
| 名称 | 华东师大版八年级上册 数学 14.2 勾股定理的应用课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 495.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 08:40:52 | ||
图片预览





文档简介
14.2 勾股定理的应用
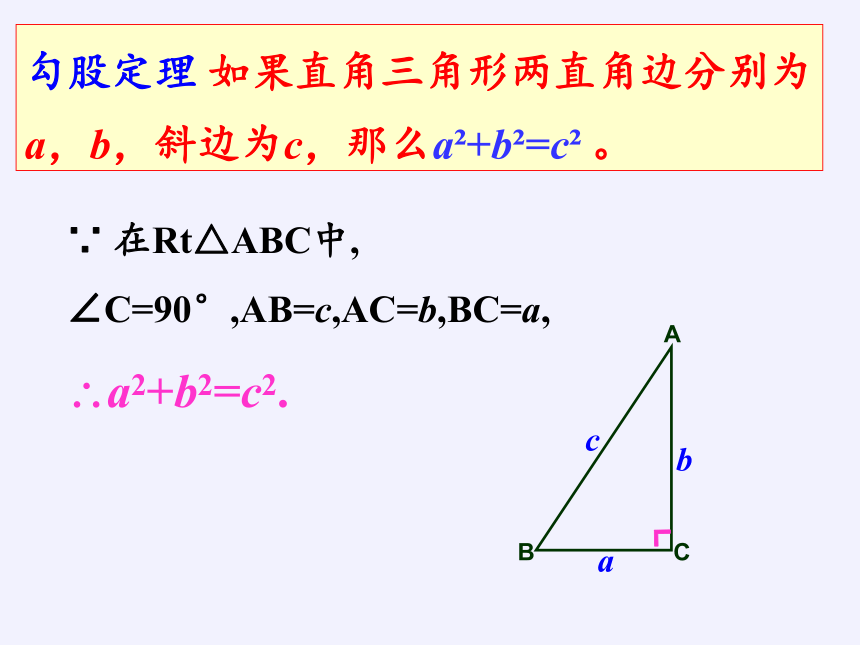
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a?+b?=c? 。
c
a
b
A
B
C
∵ 在Rt△ABC中, ∠C=90°,AB=c,AC=b,BC=a,
?a2+b2=c2.
┏
设境导入 :
?
如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
3
4
“路”
A
B
C
5
几何画板演示
4
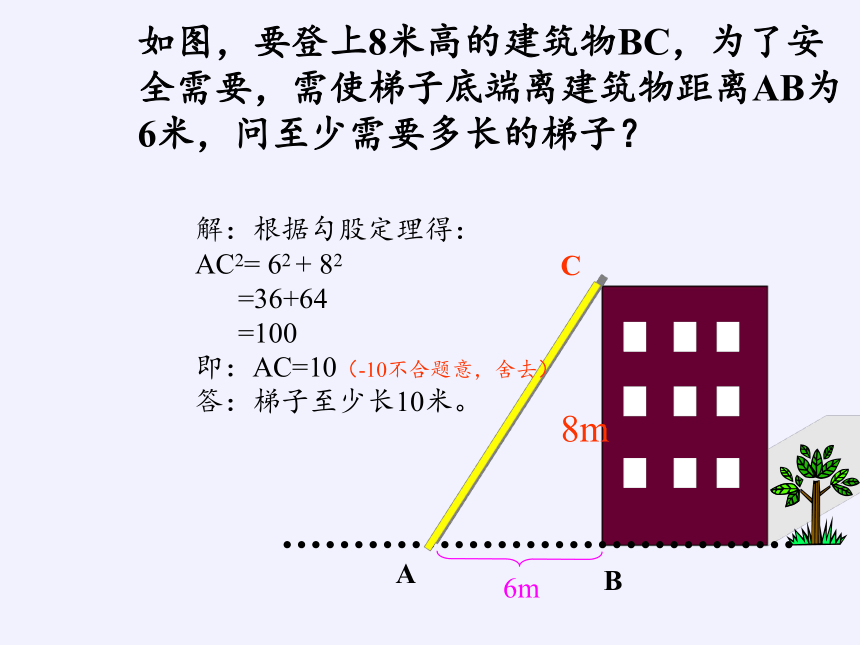
如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8m
B
C
A
6m
解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合题意,舍去)
答:梯子至少长10米。
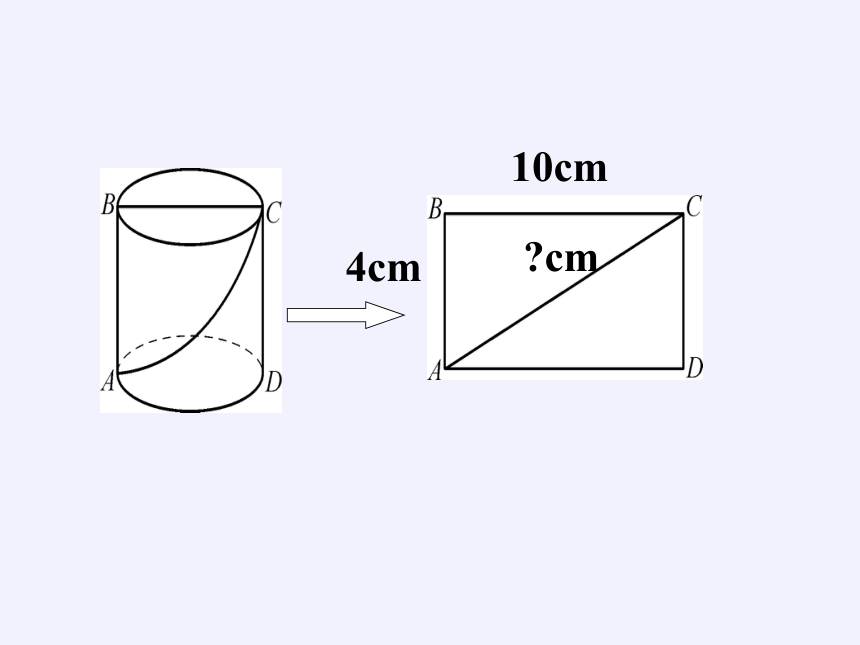
例1 如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
新知探究
(1)自制一个圆柱,尝试从A点到C点沿圆柱侧面画出几条路线,你认为哪条路线最短呢?
(2)如图,将圆柱侧面剪开展成一个长方形,从A点到C点的最短路程是什么?你画对了吗?
(3)蚂蚁从A点出发,想吃到C点上的食物,它沿圆柱侧面爬行的最短路程是多少?
10cm
4cm
?cm
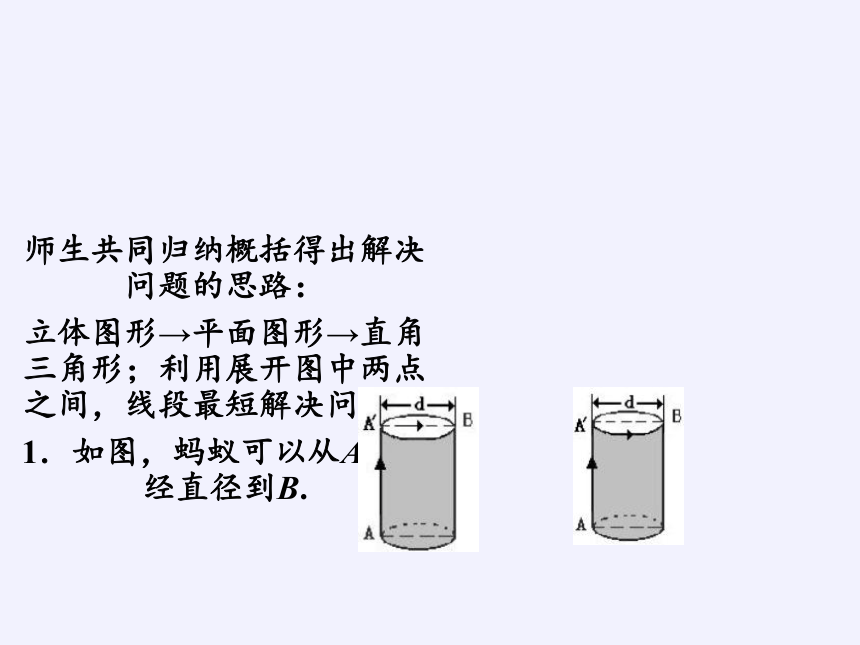
师生共同归纳概括得出解决问题的思路:
立体图形→平面图形→直角三角形;利用展开图中两点之间,线段最短解决问题。
1.如图,蚂蚁可以从A到A′经直径到B.
(1) (2)
2.如图,蚂蚁可以从A到A′经上底面圆周到B
3.情形(1)中A→B的路线长 为:A A′+d,
情形(2)中A→B的路线长为:AA′+πd/2
4.所以情形(1)的路线比情形(2)要短.
5.还有如图(3)(4)的两种情况,但我不知道如何求这两种情况的路线长度
(3) (4)
如图:
(1)中A→B的路线长为:AA′+d;
(2)中A→B的路线长为:AA′+ A′B>AB;
(3)中A→B的路线长为:AO +OB >AB;
(4)中A→B的路线长为:AB.
?? 例2
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。
A
B
C
D
2米
2.3米
A
B
M
N
O
C
┏
D
分析
H
2米
2.3米
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.
解:
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
因此高度上有0.4米的余量,所以卡车能通过厂门.
在Rt△OCD中,由勾股定理得
=
=0.6米,
A
B
M
N
O
C
┏
D
H
2米
2.3米
勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,把立体图形转换为平面图形。
如果盒子换成如图长为4cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从A点出发爬到对角顶点C1处,问怎样走路线最短?最短路程是多少?
A
C1
达标检测
4
2
1
分析:蚂蚁由A爬到C1过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
A
C1
2
4
A
B
1
C
4
2
1
B
C
A
4
2
1
B
C
A
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
A
C1
2
4
A
C1
1
AB=
=
=
5
(2)当蚂蚁经过前面和右面时,如图,最短路程为
A
B
3
2
1
B
C
A
AB=
=
=
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
A
B
AB=
=
=
4
2
1
B
C
A
∴最短路程为5cm
如果圆柱换成如图的长、宽都是3,高是8的长方体盒子,一只蚂蚁从顶点A沿着表面爬到需要爬到顶点B处,它所走的最短路程是多少?
A
B
达标检测
A
B
8
3
3
B
C
A
本节课你学到了哪些知识?
学会了解决哪些问题?
学会了哪些解决问题的方法?
你最想提出的问题是······
反馈提升
布置作业
1. 同步练习册
第69页 第三题 (1)(3)
2. 课后拓展探究题
谢 谢
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a?+b?=c? 。
c
a
b
A
B
C
∵ 在Rt△ABC中, ∠C=90°,AB=c,AC=b,BC=a,
?a2+b2=c2.
┏
设境导入 :
?
如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
3
4
“路”
A
B
C
5
几何画板演示
4
如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8m
B
C
A
6m
解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合题意,舍去)
答:梯子至少长10米。
例1 如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
新知探究
(1)自制一个圆柱,尝试从A点到C点沿圆柱侧面画出几条路线,你认为哪条路线最短呢?
(2)如图,将圆柱侧面剪开展成一个长方形,从A点到C点的最短路程是什么?你画对了吗?
(3)蚂蚁从A点出发,想吃到C点上的食物,它沿圆柱侧面爬行的最短路程是多少?
10cm
4cm
?cm
师生共同归纳概括得出解决问题的思路:
立体图形→平面图形→直角三角形;利用展开图中两点之间,线段最短解决问题。
1.如图,蚂蚁可以从A到A′经直径到B.
(1) (2)
2.如图,蚂蚁可以从A到A′经上底面圆周到B
3.情形(1)中A→B的路线长 为:A A′+d,
情形(2)中A→B的路线长为:AA′+πd/2
4.所以情形(1)的路线比情形(2)要短.
5.还有如图(3)(4)的两种情况,但我不知道如何求这两种情况的路线长度
(3) (4)
如图:
(1)中A→B的路线长为:AA′+d;
(2)中A→B的路线长为:AA′+ A′B>AB;
(3)中A→B的路线长为:AO +OB >AB;
(4)中A→B的路线长为:AB.
?? 例2
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。
A
B
C
D
2米
2.3米
A
B
M
N
O
C
┏
D
分析
H
2米
2.3米
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.
解:
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
因此高度上有0.4米的余量,所以卡车能通过厂门.
在Rt△OCD中,由勾股定理得
=
=0.6米,
A
B
M
N
O
C
┏
D
H
2米
2.3米
勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,把立体图形转换为平面图形。
如果盒子换成如图长为4cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从A点出发爬到对角顶点C1处,问怎样走路线最短?最短路程是多少?
A
C1
达标检测
4
2
1
分析:蚂蚁由A爬到C1过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
A
C1
2
4
A
B
1
C
4
2
1
B
C
A
4
2
1
B
C
A
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
A
C1
2
4
A
C1
1
AB=
=
=
5
(2)当蚂蚁经过前面和右面时,如图,最短路程为
A
B
3
2
1
B
C
A
AB=
=
=
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
A
B
AB=
=
=
4
2
1
B
C
A
∴最短路程为5cm
如果圆柱换成如图的长、宽都是3,高是8的长方体盒子,一只蚂蚁从顶点A沿着表面爬到需要爬到顶点B处,它所走的最短路程是多少?
A
B
达标检测
A
B
8
3
3
B
C
A
本节课你学到了哪些知识?
学会了解决哪些问题?
学会了哪些解决问题的方法?
你最想提出的问题是······
反馈提升
布置作业
1. 同步练习册
第69页 第三题 (1)(3)
2. 课后拓展探究题
谢 谢
