京改版七年级上册 数学 课件: 1.2 用数轴上的点表示有理数(29张)
文档属性
| 名称 | 京改版七年级上册 数学 课件: 1.2 用数轴上的点表示有理数(29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览






文档简介
1.2 用数轴上的点表示有理数
1.什么叫有理数?
答:整数和分数统称有理数。
复习
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
整数
分数
正整数
负整数
正分数
负分数
零
有理数的分类
学习目标
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.(重点)
2.会正确的画出数轴,利用数轴上的点表示有理数.(难点)
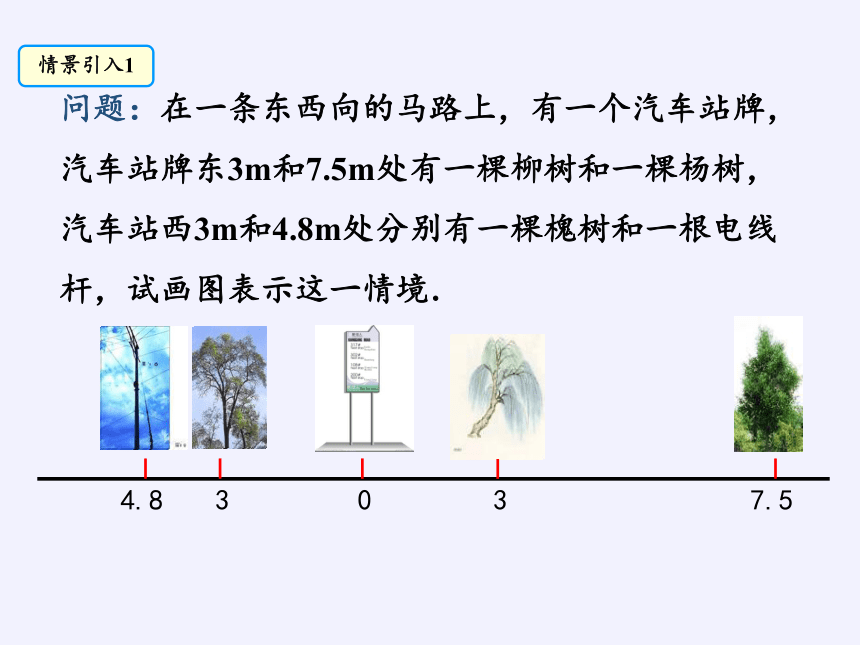
问题:在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
情景引入1
图中没有表示出来东西方向,那我们怎样表示出东西方向呢?
东西方向可以用前面我们学过的相反意义的量来表示.
0
3
7.5
3
4.8
思考:怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
为了使表达更清楚,我们规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
-4.8 -3 0 1 3 7.5
我们把正数、0和负数用一条直线上的点表示出来.
B
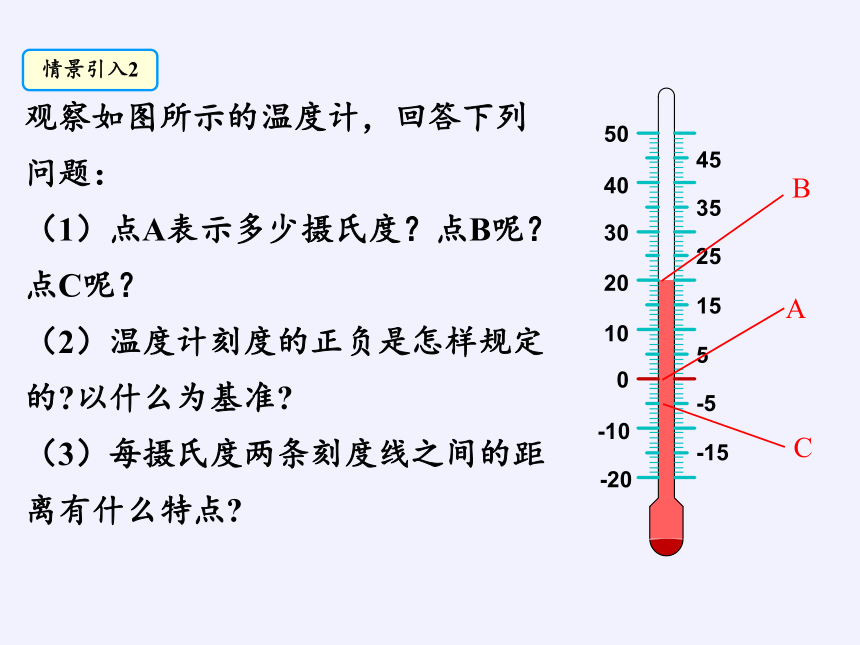
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的?以什么为基准?
(3)每摄氏度两条刻度线之间的距离有什么特点?
A
C
情景引入2
0
活动:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗?
数轴的概念
一
温度计的启示
横放的温度计
O
1
-1
-2
2
3
定义:规定了原点、正方向、单位长度的直线叫数轴.
考一考你: 数轴有哪些要素?
1、原点
2、正方向
3、单位长度
原点
正方向
单位长度
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从
原点向左)则为负方向.
3.选择适当的长度为单位长度.
?
0
0
1
2
3
-1
-2
-3
?
?
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、正方向、单位长度一个也不能少.
试一试:判断下面所画数轴是否正确,并说明理由
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻
度均匀.
画数轴注意事项:
归纳总结
0
-3 -2 -1 1 2 3
思考:
3.如何用数轴上的点来表示分数或小数?
如:1.5,- — 怎样表示.
2
3
.
.
在数轴上表示有理数
二
1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
例1 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
典例精析
任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
归纳
右
a
a
左
0
1 2
-2 -1
例2 在下面数轴上,A,B,C,D各点分别表示什么数?
D C B A
(4) D点表示-1.5
(1)A 点表示2;
(2) B 点表示0.25;
(3)C点表示-0.75;
解:
.
.
.
.
例3 从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是 ,再向右移动5个单位长度到达点C,则点C表示的数是 .
0
-3 -2 -1 1 2 3
C
.
.
解析:如图,
左移2个
右移5个
.
B
-3
2
拓展一
1. 书店A、冷饮店B、商店C依次坐落在一条东西走向的商业街上。冷饮店在书店西边20米处,商店位于书店东边100米处。小明从书店沿街向东走了40米,接着又向西走了60米,此时小明的位置在哪儿?
0
20
40
80
60
100
-20
-40
-60
-80
-100
-120
B
A
C
40米
60米
答:小明在冷饮店。
解:
0
1
2
4
3
5
-1
-2
-3
-4
-5
-6
拓展二
数轴上的点P与表示有理数3的点A距离是2
1、试确定点P表示的有理数?
2、将点A向右移动2个单位到B点,点B表示的有理 数是多少?
3、再将点B向左移动4个单位长度到C点,则点C表示的有理数是多少?
答:1、点P表示5和1;
2、点B是5;
3.点C是1
C
A
P
解:
P
2
B
4
点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-6
C.2或-6 D.不同于以上
变式训练
C
分析:点A可能向左移,也可能向右移,所以需分情况讨论.
0
1000
-2000
-1000
2000
请同学们开动你的脑筋想一想,我们选择什么的数轴,能标出1000,5000,-2000,-4000的大数呢?
5000
-4000
1000
-2000
注意:对很大(或很小)的数,我们要选适当 的单
位长度确定数轴再在数轴上标出所求的大数(或
很小)的数
拓展三
当堂练习
C
1.下列说法中正确的是( )
A. 在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C. 一个有理数总可以在数轴上找到一个表示它的点
D. 所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
2.与原点距离是2.5个单位长度的点所表示的有理数是( )
A.2.5 B.-2.5
C.±2.5 D.这个数无法确定
3.在数轴上表示数6的点在原点_____侧,到原点的距离是_____个单位长度,表示数-8的点在原点的_____侧,到原点的距离是_____个单位长度.表示数6的点
到表示数-8的点的距离是______个单位长度.
4.在数轴上到表示-2的点相距8个单位长度的点表示的数为________.
C
右
6
左
8
14
-10或6
5.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是
0,-2,1,2.5,-3.
6. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
小结
这堂课你什么收获?
你还有什么疑问?
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,0是正负数的分界点
课堂小结
谢 谢
1.什么叫有理数?
答:整数和分数统称有理数。
复习
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
整数
分数
正整数
负整数
正分数
负分数
零
有理数的分类
学习目标
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.(重点)
2.会正确的画出数轴,利用数轴上的点表示有理数.(难点)
问题:在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
情景引入1
图中没有表示出来东西方向,那我们怎样表示出东西方向呢?
东西方向可以用前面我们学过的相反意义的量来表示.
0
3
7.5
3
4.8
思考:怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
为了使表达更清楚,我们规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
-4.8 -3 0 1 3 7.5
我们把正数、0和负数用一条直线上的点表示出来.
B
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的?以什么为基准?
(3)每摄氏度两条刻度线之间的距离有什么特点?
A
C
情景引入2
0
活动:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗?
数轴的概念
一
温度计的启示
横放的温度计
O
1
-1
-2
2
3
定义:规定了原点、正方向、单位长度的直线叫数轴.
考一考你: 数轴有哪些要素?
1、原点
2、正方向
3、单位长度
原点
正方向
单位长度
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从
原点向左)则为负方向.
3.选择适当的长度为单位长度.
?
0
0
1
2
3
-1
-2
-3
?
?
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、正方向、单位长度一个也不能少.
试一试:判断下面所画数轴是否正确,并说明理由
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻
度均匀.
画数轴注意事项:
归纳总结
0
-3 -2 -1 1 2 3
思考:
3.如何用数轴上的点来表示分数或小数?
如:1.5,- — 怎样表示.
2
3
.
.
在数轴上表示有理数
二
1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
例1 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
典例精析
任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
归纳
右
a
a
左
0
1 2
-2 -1
例2 在下面数轴上,A,B,C,D各点分别表示什么数?
D C B A
(4) D点表示-1.5
(1)A 点表示2;
(2) B 点表示0.25;
(3)C点表示-0.75;
解:
.
.
.
.
例3 从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是 ,再向右移动5个单位长度到达点C,则点C表示的数是 .
0
-3 -2 -1 1 2 3
C
.
.
解析:如图,
左移2个
右移5个
.
B
-3
2
拓展一
1. 书店A、冷饮店B、商店C依次坐落在一条东西走向的商业街上。冷饮店在书店西边20米处,商店位于书店东边100米处。小明从书店沿街向东走了40米,接着又向西走了60米,此时小明的位置在哪儿?
0
20
40
80
60
100
-20
-40
-60
-80
-100
-120
B
A
C
40米
60米
答:小明在冷饮店。
解:
0
1
2
4
3
5
-1
-2
-3
-4
-5
-6
拓展二
数轴上的点P与表示有理数3的点A距离是2
1、试确定点P表示的有理数?
2、将点A向右移动2个单位到B点,点B表示的有理 数是多少?
3、再将点B向左移动4个单位长度到C点,则点C表示的有理数是多少?
答:1、点P表示5和1;
2、点B是5;
3.点C是1
C
A
P
解:
P
2
B
4
点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-6
C.2或-6 D.不同于以上
变式训练
C
分析:点A可能向左移,也可能向右移,所以需分情况讨论.
0
1000
-2000
-1000
2000
请同学们开动你的脑筋想一想,我们选择什么的数轴,能标出1000,5000,-2000,-4000的大数呢?
5000
-4000
1000
-2000
注意:对很大(或很小)的数,我们要选适当 的单
位长度确定数轴再在数轴上标出所求的大数(或
很小)的数
拓展三
当堂练习
C
1.下列说法中正确的是( )
A. 在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C. 一个有理数总可以在数轴上找到一个表示它的点
D. 所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
2.与原点距离是2.5个单位长度的点所表示的有理数是( )
A.2.5 B.-2.5
C.±2.5 D.这个数无法确定
3.在数轴上表示数6的点在原点_____侧,到原点的距离是_____个单位长度,表示数-8的点在原点的_____侧,到原点的距离是_____个单位长度.表示数6的点
到表示数-8的点的距离是______个单位长度.
4.在数轴上到表示-2的点相距8个单位长度的点表示的数为________.
C
右
6
左
8
14
-10或6
5.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是
0,-2,1,2.5,-3.
6. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
小结
这堂课你什么收获?
你还有什么疑问?
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,0是正负数的分界点
课堂小结
谢 谢
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
