京改版八年级上册 数学 课件: 12.11 勾股定理(24张)
文档属性
| 名称 | 京改版八年级上册 数学 课件: 12.11 勾股定理(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 928.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览







文档简介
12.11 勾股定理
情境引入
在古老的数学王国,有一种树木它很奇妙,生长速度大的惊人,它是什么呢?下面让我们带着这个疑问一同到数学王国去欣赏吧!
学习目标
1
2
认识勾股定理,利用勾股定理进行简单的计算和实际运用;
3
体会数形结合思想和化归思想的运用,增强解决问题的能力;
进一步丰富数学活动经验,锻炼推理能力,感受勾股定理的文化价值.
自主学习任务1:阅读课本2页-3页,掌握下列知识要点。
课前自主学习
勾股定理的内容是什么?
本节课我们用什么方法发现了勾股定理?
上述方法体现了什么数学思想?
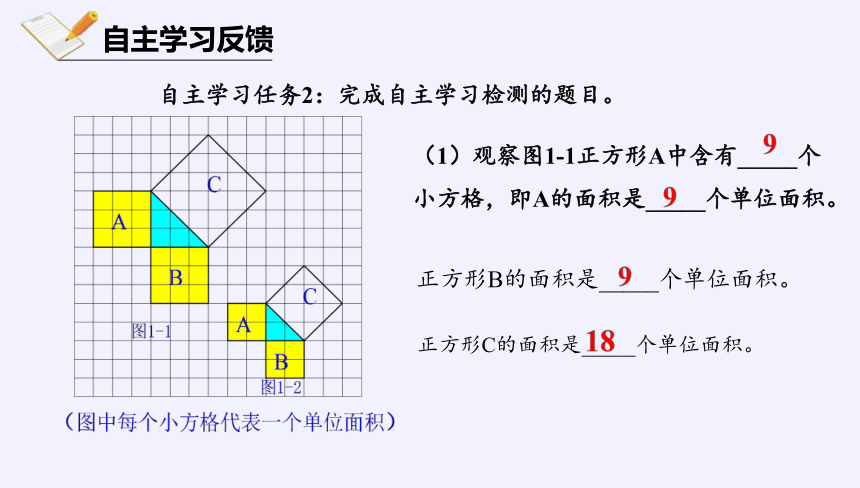
自主学习任务2:完成自主学习检测的题目。
自主学习反馈
(1)观察图1-1正方形A中含有_____个小方格,即A的面积是_____个单位面积。
正方形B的面积是_____个单位面积。
正方形C的面积是_____个单位面积。
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积S1、S2、S3之间有什么关系吗?
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。
自主学习反馈
自主学习任务2:完成自主学习检测的题目。
4,4,8
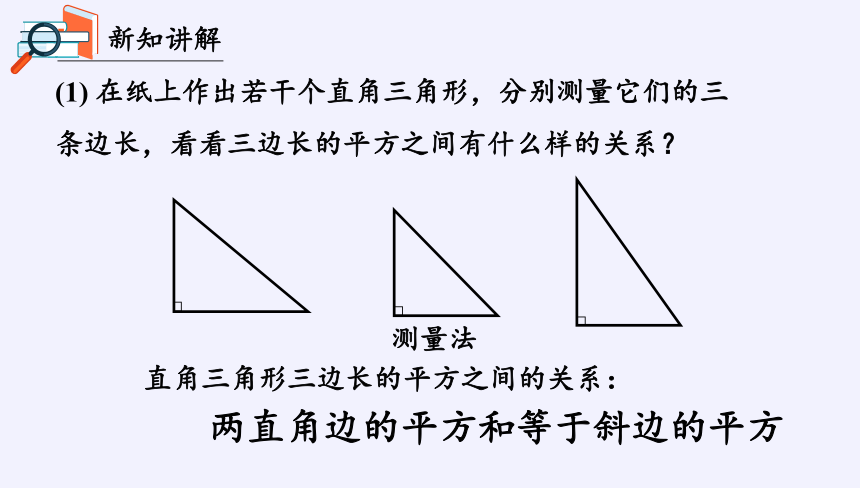
(1) 在纸上作出若干个直角三角形,分别测量它们的三条边长,看看三边长的平方之间有什么样的关系?
直角三角形三边长的平方之间的关系:
两直角边的平方和等于斜边的平方
测量法
新知讲解
(2) 如图,直角三角形三边的平方分别是多少,它们满足上面所猜想的数量关系?你是如何计算的?
ⅰ、三边的平方分别是
各正方形的面积;
ⅱ、满足“两直角边的平
方和等于斜边的平方”。
数格子法
新知讲解
新知讲解
一般的直角三角形,上述
结论成立吗?
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理
新知讲解
如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
解:在Rt△ABC中,由勾股定理得,
AB?=AC?+BC?,
AB2=122+52.
∴AB2=169.
∴AB=13.
答:斜边AB的长度为13厘米 .
新知讲解
做一做下面的题目,看谁做得又快又准确。
分层教学
A组
B组
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.
求CD的长.
争先恐后
我来
我来
我来
我来
小组展示
归纳:已知直角三角形的两边,求第三边,是勾股定理的一个重要应用.
解析一览
解:∵ ∠ACB=90°,AC=3,BC=4,
∴ AB2=AC2+BC2=25,
即AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
?=325
x=8
1.求下列图中字母所表示的正方形的面积
=625
随堂检测
2.阴影部分是一个正方形,则此正方形的面积为_______.
随堂检测
3. 小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你能解释这是为什么吗?
随堂检测
学以致用
分组探讨学习,看哪个组做得又快又准确。
A组
B组
一直角三角形的两边长分别是3和4,则第三边长的平方为( )
A.25 B .7
C.5 D 25或7.
一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解析一览
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7.
归纳:应用勾股定理的前提是直角三角形,即只有在直角三角形中,三边才满足关系式a2+b2=c2,尤其注意斜边的确定.
一直角三角形的两边长分别是3和4,则第三边长的平方为( )
A.25 B .7
C.5 D. 25或7
D
1、勾股定理:
直角三角形两直角边的平方和等于斜边的平方。
2、验证“勾股定理”的方法:
(1)测量法
(2)数格子法
3、“勾股定理”的应用:
已知直角三角形两边,求第三边。
课堂小结
定理内容
勾股
定理
定理运用
重要的思想方法及数学思想
从特殊到一般、数形结合思想
课堂小结
个性化作业
1.完成八年级上册1.1.1探索勾股定理A组 课后作业。
2.预习课本4页-6页,完成1.1.2探索勾股定理自主学习检测题目。
1.完成八年级上册1.1.1探索勾股定理B组 课后作业。
2.预习课本4页-6页,完成1.1.2探索勾股定理自主学习检测题目。
A组
B组
谢 谢
情境引入
在古老的数学王国,有一种树木它很奇妙,生长速度大的惊人,它是什么呢?下面让我们带着这个疑问一同到数学王国去欣赏吧!
学习目标
1
2
认识勾股定理,利用勾股定理进行简单的计算和实际运用;
3
体会数形结合思想和化归思想的运用,增强解决问题的能力;
进一步丰富数学活动经验,锻炼推理能力,感受勾股定理的文化价值.
自主学习任务1:阅读课本2页-3页,掌握下列知识要点。
课前自主学习
勾股定理的内容是什么?
本节课我们用什么方法发现了勾股定理?
上述方法体现了什么数学思想?
自主学习任务2:完成自主学习检测的题目。
自主学习反馈
(1)观察图1-1正方形A中含有_____个小方格,即A的面积是_____个单位面积。
正方形B的面积是_____个单位面积。
正方形C的面积是_____个单位面积。
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积S1、S2、S3之间有什么关系吗?
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。
自主学习反馈
自主学习任务2:完成自主学习检测的题目。
4,4,8
(1) 在纸上作出若干个直角三角形,分别测量它们的三条边长,看看三边长的平方之间有什么样的关系?
直角三角形三边长的平方之间的关系:
两直角边的平方和等于斜边的平方
测量法
新知讲解
(2) 如图,直角三角形三边的平方分别是多少,它们满足上面所猜想的数量关系?你是如何计算的?
ⅰ、三边的平方分别是
各正方形的面积;
ⅱ、满足“两直角边的平
方和等于斜边的平方”。
数格子法
新知讲解
新知讲解
一般的直角三角形,上述
结论成立吗?
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理
新知讲解
如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
解:在Rt△ABC中,由勾股定理得,
AB?=AC?+BC?,
AB2=122+52.
∴AB2=169.
∴AB=13.
答:斜边AB的长度为13厘米 .
新知讲解
做一做下面的题目,看谁做得又快又准确。
分层教学
A组
B组
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.
求CD的长.
争先恐后
我来
我来
我来
我来
小组展示
归纳:已知直角三角形的两边,求第三边,是勾股定理的一个重要应用.
解析一览
解:∵ ∠ACB=90°,AC=3,BC=4,
∴ AB2=AC2+BC2=25,
即AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
?=325
x=8
1.求下列图中字母所表示的正方形的面积
=625
随堂检测
2.阴影部分是一个正方形,则此正方形的面积为_______.
随堂检测
3. 小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你能解释这是为什么吗?
随堂检测
学以致用
分组探讨学习,看哪个组做得又快又准确。
A组
B组
一直角三角形的两边长分别是3和4,则第三边长的平方为( )
A.25 B .7
C.5 D 25或7.
一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解析一览
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7.
归纳:应用勾股定理的前提是直角三角形,即只有在直角三角形中,三边才满足关系式a2+b2=c2,尤其注意斜边的确定.
一直角三角形的两边长分别是3和4,则第三边长的平方为( )
A.25 B .7
C.5 D. 25或7
D
1、勾股定理:
直角三角形两直角边的平方和等于斜边的平方。
2、验证“勾股定理”的方法:
(1)测量法
(2)数格子法
3、“勾股定理”的应用:
已知直角三角形两边,求第三边。
课堂小结
定理内容
勾股
定理
定理运用
重要的思想方法及数学思想
从特殊到一般、数形结合思想
课堂小结
个性化作业
1.完成八年级上册1.1.1探索勾股定理A组 课后作业。
2.预习课本4页-6页,完成1.1.2探索勾股定理自主学习检测题目。
1.完成八年级上册1.1.1探索勾股定理B组 课后作业。
2.预习课本4页-6页,完成1.1.2探索勾股定理自主学习检测题目。
A组
B组
谢 谢
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
