苏科版八年级上册 数学 课件: 2.4 线段、角的轴对称性(17张)
文档属性
| 名称 | 苏科版八年级上册 数学 课件: 2.4 线段、角的轴对称性(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览





文档简介
2.4 线段、角的轴对称性
(1)折痕MN与线段AB的位置关系是________________;
直线MN垂直平分AB
是
PA=PB
活动1
在纸上画一条线段AB,如图,折纸使两个端点A、B重合.
(2)线段AB________(填“是”或“不是”)轴对称图形;
(3)在折痕上找一点P,连接PA,PB.再次沿MN折叠,PA与PB的关系是__________.
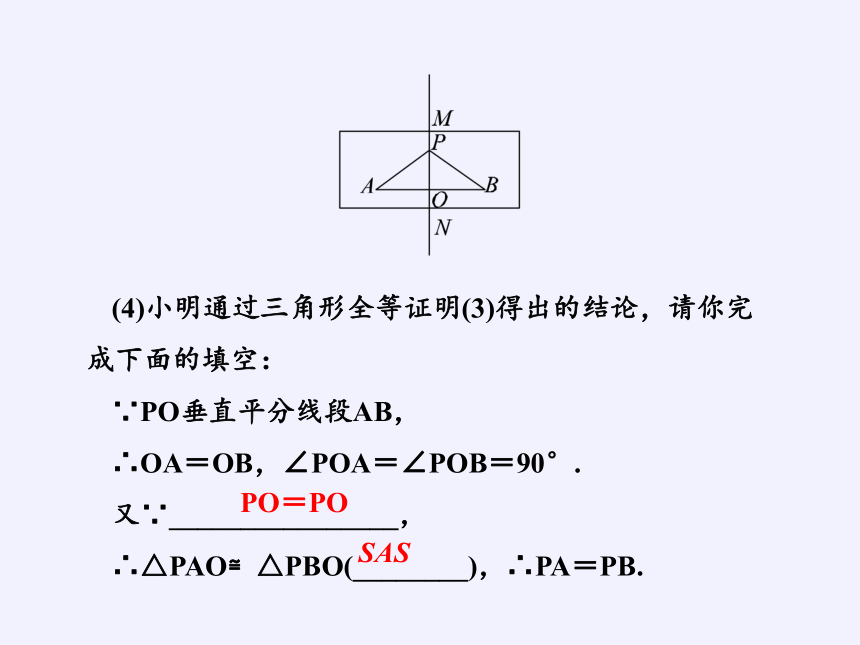
(4)小明通过三角形全等证明(3)得出的结论,请你完成下面的填空:
∵PO垂直平分线段AB,
∴OA=OB,∠POA=∠POB=90°.
又∵________________,
∴△PAO≌△PBO(________),∴PA=PB.
PO=PO
SAS
[答案]小明考虑的不够全面,当P点在线段AB上时,点P为AB的中点,故PA=PB,此时不存在上面的全等三角形,P不在AB上时,才可以用小明的方法证明.
小明考虑的全面吗?为什么?
你能运用图形运动的方法,说明上述结论吗?
[答案]把△PAO沿直线MN翻折,因为∠PAO=∠POB,所以OA落在射线OB上.因为OA=OB,所以点A与点B重合.依据基本事实“两点确定一条直线”,可知PA与PB重合,所以PA=PB.
知识梳理
线段的轴对称性:线段是________图形,线段的____________是它的对称轴.
线段的垂直平分线的性质:线段垂直平分线上的点到________
_______________.
轴对称
垂直平分线
线段两端
的距离相等
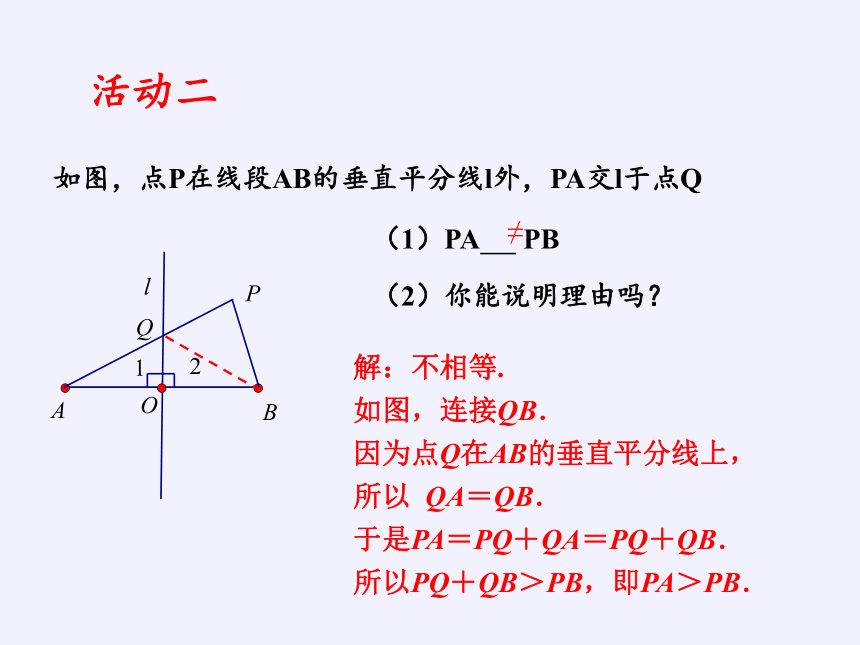
如图,点P在线段AB的垂直平分线l外,PA交l于点Q
活动二
解:不相等.
如图,连接QB.
因为点Q在AB的垂直平分线上,
所以 QA=QB.
于是PA=PQ+QA=PQ+QB.
所以PQ+QB>PB,即PA>PB.
O
2
1
l
B
A
P
Q
(1)PA PB
≠
(2)你能说明理由吗?
例题精讲
例1、如图,在△ABC中,AB+AC=6 cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为多少?
[变式]如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N.若△BCN的周长是7 cm,求BC的长
例题精讲
例题精讲
例2、如图,要在公路旁设一个公交车的停车站,停车站应设在什么地方,才能使A、B两村到车站的距离相等?
[变式]如图,要在公路旁设一个公共汽车站,车站应建在什么地方,才能使A、B两村到车站的距离相等?
例题精讲
例3、利用网格线画线段PQ的垂直平分线.
例题精讲
当堂检测
1.如图1,PO是AB的垂直平分线,则下列结论:①PA=PB,②OA=OB,③∠A=∠B,④∠APO=∠BPO.其中正确的有( )
A.①②③ B.①②④ C.①②③④ D.②③④
2.如图2,△ABC的垂直平分线DE交AB于点E,交BC于点D,连接AD,已知AC=5 cm,△ADC的周长为17 cm,则BC的长为________ cm.
3.如图3,在正方形方格纸上有一个△ABC,利用网格在BC边上确定一个到A,B距离相等的点D.
4.如图4,OM垂直平分AB,ON垂直平分AC,BC分别交OM,ON于点D,E.
(1)若BC=10,求△ADE的周长;
(2)连接OB,OC,则OB与OC有什么数量关系?为什么?
说说你本节课你有什么收获?
课堂小结
伴你学 2.4(1)随堂练习
迁移运用(选做)
课后作业
1.如图,在△ABC中,AB=AC,D是AB边的中点,且DE⊥AB,△BCE的周长为8 cm,且AC-BC=2 cm,求AB,BC的长.
2.如图,在△ABC中,D是BC边的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,交AB于点E,连接EG.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并证明你的结论.
拓展延伸
谢 谢
(1)折痕MN与线段AB的位置关系是________________;
直线MN垂直平分AB
是
PA=PB
活动1
在纸上画一条线段AB,如图,折纸使两个端点A、B重合.
(2)线段AB________(填“是”或“不是”)轴对称图形;
(3)在折痕上找一点P,连接PA,PB.再次沿MN折叠,PA与PB的关系是__________.
(4)小明通过三角形全等证明(3)得出的结论,请你完成下面的填空:
∵PO垂直平分线段AB,
∴OA=OB,∠POA=∠POB=90°.
又∵________________,
∴△PAO≌△PBO(________),∴PA=PB.
PO=PO
SAS
[答案]小明考虑的不够全面,当P点在线段AB上时,点P为AB的中点,故PA=PB,此时不存在上面的全等三角形,P不在AB上时,才可以用小明的方法证明.
小明考虑的全面吗?为什么?
你能运用图形运动的方法,说明上述结论吗?
[答案]把△PAO沿直线MN翻折,因为∠PAO=∠POB,所以OA落在射线OB上.因为OA=OB,所以点A与点B重合.依据基本事实“两点确定一条直线”,可知PA与PB重合,所以PA=PB.
知识梳理
线段的轴对称性:线段是________图形,线段的____________是它的对称轴.
线段的垂直平分线的性质:线段垂直平分线上的点到________
_______________.
轴对称
垂直平分线
线段两端
的距离相等
如图,点P在线段AB的垂直平分线l外,PA交l于点Q
活动二
解:不相等.
如图,连接QB.
因为点Q在AB的垂直平分线上,
所以 QA=QB.
于是PA=PQ+QA=PQ+QB.
所以PQ+QB>PB,即PA>PB.
O
2
1
l
B
A
P
Q
(1)PA PB
≠
(2)你能说明理由吗?
例题精讲
例1、如图,在△ABC中,AB+AC=6 cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为多少?
[变式]如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N.若△BCN的周长是7 cm,求BC的长
例题精讲
例题精讲
例2、如图,要在公路旁设一个公交车的停车站,停车站应设在什么地方,才能使A、B两村到车站的距离相等?
[变式]如图,要在公路旁设一个公共汽车站,车站应建在什么地方,才能使A、B两村到车站的距离相等?
例题精讲
例3、利用网格线画线段PQ的垂直平分线.
例题精讲
当堂检测
1.如图1,PO是AB的垂直平分线,则下列结论:①PA=PB,②OA=OB,③∠A=∠B,④∠APO=∠BPO.其中正确的有( )
A.①②③ B.①②④ C.①②③④ D.②③④
2.如图2,△ABC的垂直平分线DE交AB于点E,交BC于点D,连接AD,已知AC=5 cm,△ADC的周长为17 cm,则BC的长为________ cm.
3.如图3,在正方形方格纸上有一个△ABC,利用网格在BC边上确定一个到A,B距离相等的点D.
4.如图4,OM垂直平分AB,ON垂直平分AC,BC分别交OM,ON于点D,E.
(1)若BC=10,求△ADE的周长;
(2)连接OB,OC,则OB与OC有什么数量关系?为什么?
说说你本节课你有什么收获?
课堂小结
伴你学 2.4(1)随堂练习
迁移运用(选做)
课后作业
1.如图,在△ABC中,AB=AC,D是AB边的中点,且DE⊥AB,△BCE的周长为8 cm,且AC-BC=2 cm,求AB,BC的长.
2.如图,在△ABC中,D是BC边的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,交AB于点E,连接EG.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并证明你的结论.
拓展延伸
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
