苏科版八年级上册 数学 课件 :2.5 等腰三角形的轴对称性(13张)
文档属性
| 名称 | 苏科版八年级上册 数学 课件 :2.5 等腰三角形的轴对称性(13张) |  | |
| 格式 | pptx | ||
| 文件大小 | 487.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 14:34:10 | ||
图片预览




文档简介
2.5 等腰三角形的轴对称性
【情境引入】
1. 任意一个三角形是轴对称图形吗?
3.怎样验证你的想法是正确的呢?
2. 当三角形满足什么条件时才是轴对称图形呢?
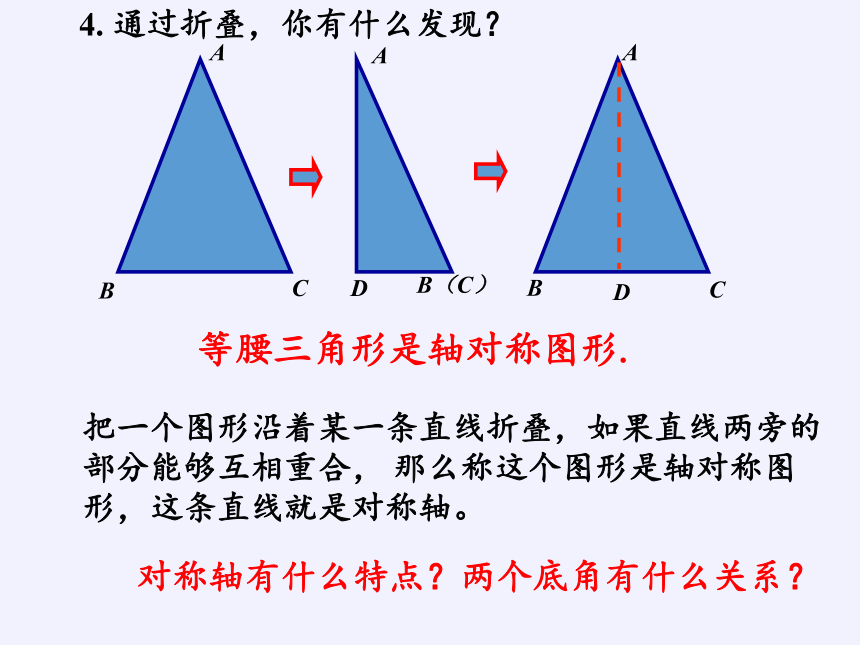
4. 通过折叠,你有什么发现?
A
B
C
A
D
B(C)
A
B
C
D
等腰三角形是轴对称图形.
把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合, 那么称这个图形是轴对称图形,这条直线就是对称轴。
对称轴有什么特点?两个底角有什么关系?
【归纳总结】
1.等腰三角形的两底角相等。
思考:如何证明我们的发现?
2.等腰三角形底边上的高线、中线及顶角平分线重合。
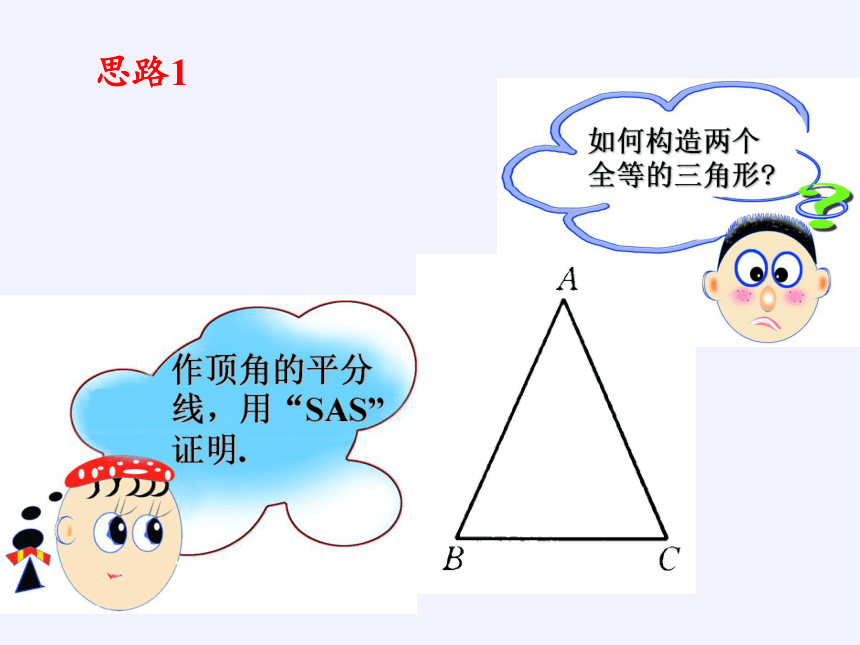
如何构造两个全等的三角形?
作顶角的平分线,用“SAS”证明.
思路1
A
B
C
则有∠1=∠2,
D
1
2
在△ABD和△ACD中,
证明:作顶角的平分线AD,
AB=AC,
∠1=∠2,
AD=AD
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等).
BD=CD (全等三角形对应边相等).
(即AD是BC边上的中线)
∠ ADB=∠ADC=90°
(即AD是BC边上的高)
思考:你还可用什么方法证明上述定理?
也可作底边上的高,用“HL”证明.
作底边上的中线,用“SSS”证明.
1.等腰三角形的两底角相等(简称“等边对等角”)
【归纳总结】
因为AB=AC
2.等腰三角形底边上的高线、中线及顶角平分线重合。 (简称“三线合一”)
(1)因为AB=AC , ∠B AD=∠CAD
(2)因为AB=AC , BD=CD
(3)因为AB=AC , AD ┴ BC
所以∠B=∠C
所以BD=CD ,AD ┴ BC
所以∠B AD=∠CAD, AD ┴ BC
所以∠B AD=∠CAD, BD=CD
练一练:
在△ABC中,AB=AC.
⑴ 如果∠B=70°,那么∠C=___,∠A=____.
⑵ 如果∠A=70°,那么∠B=____,∠C= ___.
⑶ 如果有一个角等于120°,
那么∠A=___ °,∠B=___ °,∠C =___ °.
⑷ 如果有一个角等于50°,那么另两个角等于多少度?
【例题讲解 】
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
1
2
1.如图的房屋人字梁架中,AB=AC ,AD⊥BC, ∠BAC=110°,求∠B、∠C 、∠BAD、∠CAD的度数.
试一试
【课堂小结】
通过本节课学习你有什么收获?
(1)思考问题的方法
(2)知识点归纳
谢 谢
【情境引入】
1. 任意一个三角形是轴对称图形吗?
3.怎样验证你的想法是正确的呢?
2. 当三角形满足什么条件时才是轴对称图形呢?
4. 通过折叠,你有什么发现?
A
B
C
A
D
B(C)
A
B
C
D
等腰三角形是轴对称图形.
把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合, 那么称这个图形是轴对称图形,这条直线就是对称轴。
对称轴有什么特点?两个底角有什么关系?
【归纳总结】
1.等腰三角形的两底角相等。
思考:如何证明我们的发现?
2.等腰三角形底边上的高线、中线及顶角平分线重合。
如何构造两个全等的三角形?
作顶角的平分线,用“SAS”证明.
思路1
A
B
C
则有∠1=∠2,
D
1
2
在△ABD和△ACD中,
证明:作顶角的平分线AD,
AB=AC,
∠1=∠2,
AD=AD
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等).
BD=CD (全等三角形对应边相等).
(即AD是BC边上的中线)
∠ ADB=∠ADC=90°
(即AD是BC边上的高)
思考:你还可用什么方法证明上述定理?
也可作底边上的高,用“HL”证明.
作底边上的中线,用“SSS”证明.
1.等腰三角形的两底角相等(简称“等边对等角”)
【归纳总结】
因为AB=AC
2.等腰三角形底边上的高线、中线及顶角平分线重合。 (简称“三线合一”)
(1)因为AB=AC , ∠B AD=∠CAD
(2)因为AB=AC , BD=CD
(3)因为AB=AC , AD ┴ BC
所以∠B=∠C
所以BD=CD ,AD ┴ BC
所以∠B AD=∠CAD, AD ┴ BC
所以∠B AD=∠CAD, BD=CD
练一练:
在△ABC中,AB=AC.
⑴ 如果∠B=70°,那么∠C=___,∠A=____.
⑵ 如果∠A=70°,那么∠B=____,∠C= ___.
⑶ 如果有一个角等于120°,
那么∠A=___ °,∠B=___ °,∠C =___ °.
⑷ 如果有一个角等于50°,那么另两个角等于多少度?
【例题讲解 】
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
1
2
1.如图的房屋人字梁架中,AB=AC ,AD⊥BC, ∠BAC=110°,求∠B、∠C 、∠BAD、∠CAD的度数.
试一试
【课堂小结】
通过本节课学习你有什么收获?
(1)思考问题的方法
(2)知识点归纳
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
