苏科版八年级上册 数学6.1 函数 课件 (30张ppt)
文档属性
| 名称 | 苏科版八年级上册 数学6.1 函数 课件 (30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览









文档简介
6.1 函数
我们生活在一个瞬息万变的世界里,在这个世界里,许多东西相互之间是有一定联系的.今天,就让我们用数学的眼睛,来一同观察这些“变化”与“联系”......
我们的学习从这里开始……
国庆黄金周天气晴朗,小薇一家开着车去苏州舅舅家作客.请同学们一起跟随小薇踏上旅程,开始我们今天的探索与学习.
在加油的过程中,哪些量是变化的,哪些量是不变的
油的单价不变
油量是变化的,金额是变化的
观察
在某一变化过程中,
数值保持不变的量叫做常量;
可以取不同数值的量叫做变量.
相信你能认识
1.汽车以60 km/h 的速度匀速行驶,行驶时间为 t h,行驶路程为 s km.
常量: ,
变量: .
60
t ,s
试一试
找出下面问题中常量和变量:
2.圆形水波慢慢地扩大,在这一变化的过程中,当圆的半径为r ,圆的面积为S ,在这个变化的过程中,变化的量是?
r,s
变量: .
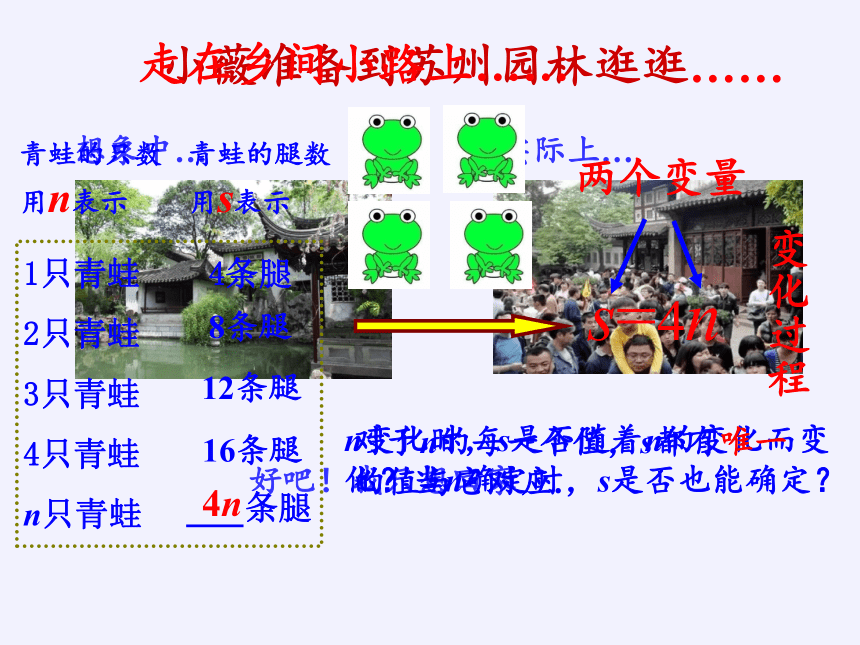
小薇准备到苏州园林逛逛……
想象中…
实际上…
好吧!我只想回家
s=4n
4n
8条腿
12条腿
16条腿
两个变量
青蛙的只数用n表示
青蛙的腿数用s表示
1只青蛙 4条腿
2只青蛙
3只青蛙
4只青蛙
n只青蛙
条腿
变化过程
n变化时,s是否随着n的变化而变化?当n确定时,s是否也能确定?
对于n的每一个值,s都有唯一的值与它对应.
走在乡间小路上……
小薇数着青蛙往舅舅家走去……
在门口碰到了做作业的表弟,貌似小表弟在做数学,表弟是这样做的:
同学们,你们觉得对吗?
为了让表弟改正自己的错误,小薇随即列了一张表格让表弟填写:
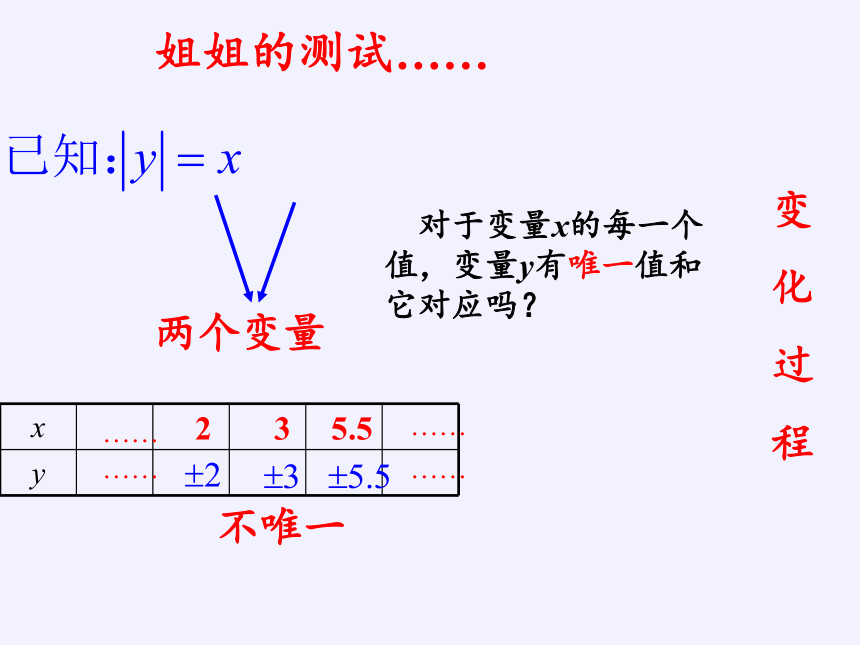
x
y
2
3
5.5
……
两个变量
对于变量x的每一个值,变量y有唯一值和它对应吗?
……
……
……
变
化
过
程
不唯一
姐姐的测试……
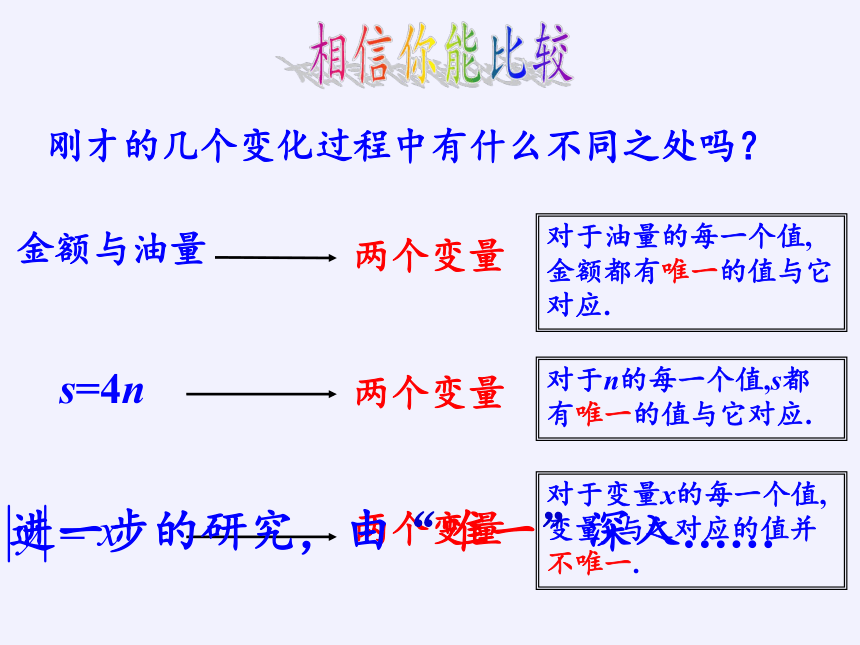
相信你能比较
刚才的几个变化过程中有什么不同之处吗?
s=4n
两个变量
两个变量
对于n的每一个值,s都有唯一的值与它对应.
对于变量x的每一个值,变量y与之对应的值并不唯一.
金额与油量
两个变量
对于油量的每一个值,金额都有唯一的值与它对应.
进一步的研究,由“唯一”深入……
新中国成立以来,我国已经进行了六次人口普查. 下表是我国六次人口普查的人口数统计表.
年份
人口数(亿)
1953
6.02
1964
7.23
1982
10.32
1990
11.60
2000
12.95
2010
13.71
(1)在这一变化过程中,有几个变量?分别是什么?
(2)在这一变化过程中,两个变量之间有什么关系?
随着 的变化而变化.
人口数
年份
对于 的每一个值, 都有唯一的值与它对应.
年份
人口数
饭后铺在桌上的一张旧报纸引起了小薇的注意……
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
下图是苏州冬季一天的气温变化曲线.
随着 的变化而变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于 的每一个值, 都有唯一的值与它对应.
在这一变化过程中,两个变量之间有什么关系?
温度
时间
时间
温度
?
?
?
同学们,你们能从刚才的几个变化过程中找到它们的共同之处吗?
对于 的每一个值,
有_____值与之对应.
S=4n
相信你能发现
金额与油量
两
唯一
随之变化
人口数与年份
温度T与时间t
每个变化过程中都有___个变量,
其中 变化时,
也___________;
x 和 y
x
y
x
y
一个变量
另一个变量
其中一个变量
另一个变量
其中,x是自变量, y是因变量.
一般地, 在一个变化过程中的两个变量x和y,如果对于x的每一个值, y都有唯一的值与它对应,那么我们称y是x的函数.
相信你能理解
函数小史
function
莱布尼兹
(德国)
李善兰
(清代)
凡此变数函彼变数,则此为彼之函数 .
(这里的“函”有包含的意思.)
函数
翻译
S =4n
金额与油量
金额是油量的函数吗?
想一想
s是n的函数吗?
年份
人口数(亿)
1953
6.02
1964
7.23
1982
10.32
1990
11.60
2000
12.95
2010
13.71
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
人口数是年份的函数吗?
温度T是时间t的函数吗?
中,y是x的函数吗?
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
解析法
列表法
图像法
函数的三种表示方法
S =4n
年份
人口数(亿)
1953
6.02
1964
7.23
1982
10.32
1990
11.60
2000
12.95
2010
13.71
(函数解析式)
舅舅说最近村子里有黄鼠狼,小薇准备帮助舅舅用一段20m长的栅栏围一个长方形鸡舍……
(1)当长方形的宽为2m时,长为 ____ m;
(2)当长方形的宽为4m时,长为 ____ m;
(3)当长方形的宽为b m时,长为 ______ m.
8
6
(10-b)
(4)长方形的长是宽的函数吗?为什么?
帮舅舅围鸡舍……
(5)长方形的宽是长的函数吗?为什么?
(6)长方形的面积是宽的函数吗?为什么?
我们的探索和研究也接近尾声,
下面就请同学们运用函数的概念
来解决几个小问题.
忙碌中,小薇假期的一天结束了
1.下列表格反映了一个变化过程中y与x的关系,其中y 是x的函数吗?
(2)
(1)
练一练
2.在平行四边形面积公式 (a表示平行四边形的底,h表示底边上的高),若a固定,h是自变量,则a是____量,而面积S是____的函数;若h固定,a是自变量,则常量是____,而面积S是____的函数;
常
h
h
a
练一练
若S 固定,则常量是____,____是____的函数
3.(1)若每吨民用自来水的价格为2.8元,所交水 费金额为y(元),使用自来水的数量为x(吨),
则 y 是 x 的函数吗?为什么?
(2)底边为6(m)的三角形面积为s(㎡),高为h (m), s是h的函数吗?为什么?
练一练
?
?
4.根据小鱼的条数与所需火柴棒的根数的关系,
说说你从中获得的信息.
6n+2
s=6n+2
……
……
8
14
20
n
火柴的根数(s)
小鱼条数(n)
2
1
3
……
……
练一练
5.为了加强居民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水x吨(x>10),应交水费y元.请求出y和x的表达式,并判断y是否为x的函数.
练一练
y =12+1.8(x-10)
=1.8x-6
6.用60m的篱笆围成长方形,使长方形一边靠墙
(墙足够长),另三边用篱笆围成
墙
a
a
b
(3)写出长方形面积s(m2)与平行于墙的一边长
b(m)的关系式;
(4)并指出上式中的函数与自变量.
(1)写出长方形面积s(m2)与垂直于墙的一边长
a(m)的关系式;
(2)指出上式中的函数与自变量.
练一练
小结
2.函数:
1.常量和变量:
在某一变化过程中,数值保持不变的量叫做常量;
可以取不同数值的量叫做变量.
一般地,设在一个变化的过程中有两个变量x和y,
并且对于变量x的每一个值,变量y都有唯一的值
与它对应,那么我们称y是x的函数(function).
其中,x是自变量,y是因变量.
自己找一个实际生活中表示函数关系例子.
小组交流的要求:
每个人轮流说说自己编的函数实例,推荐一名同学准备班级交流.
相信你能应用
时间是一个“变量”,愿你们在飞驰而去的时间波涛上,乘风破浪,驶向成功的彼岸;
人生也是个“变量”,愿你们在前行的道路上,用自己的双手建造幸运的大厦。
谢 谢
我们生活在一个瞬息万变的世界里,在这个世界里,许多东西相互之间是有一定联系的.今天,就让我们用数学的眼睛,来一同观察这些“变化”与“联系”......
我们的学习从这里开始……
国庆黄金周天气晴朗,小薇一家开着车去苏州舅舅家作客.请同学们一起跟随小薇踏上旅程,开始我们今天的探索与学习.
在加油的过程中,哪些量是变化的,哪些量是不变的
油的单价不变
油量是变化的,金额是变化的
观察
在某一变化过程中,
数值保持不变的量叫做常量;
可以取不同数值的量叫做变量.
相信你能认识
1.汽车以60 km/h 的速度匀速行驶,行驶时间为 t h,行驶路程为 s km.
常量: ,
变量: .
60
t ,s
试一试
找出下面问题中常量和变量:
2.圆形水波慢慢地扩大,在这一变化的过程中,当圆的半径为r ,圆的面积为S ,在这个变化的过程中,变化的量是?
r,s
变量: .
小薇准备到苏州园林逛逛……
想象中…
实际上…
好吧!我只想回家
s=4n
4n
8条腿
12条腿
16条腿
两个变量
青蛙的只数用n表示
青蛙的腿数用s表示
1只青蛙 4条腿
2只青蛙
3只青蛙
4只青蛙
n只青蛙
条腿
变化过程
n变化时,s是否随着n的变化而变化?当n确定时,s是否也能确定?
对于n的每一个值,s都有唯一的值与它对应.
走在乡间小路上……
小薇数着青蛙往舅舅家走去……
在门口碰到了做作业的表弟,貌似小表弟在做数学,表弟是这样做的:
同学们,你们觉得对吗?
为了让表弟改正自己的错误,小薇随即列了一张表格让表弟填写:
x
y
2
3
5.5
……
两个变量
对于变量x的每一个值,变量y有唯一值和它对应吗?
……
……
……
变
化
过
程
不唯一
姐姐的测试……
相信你能比较
刚才的几个变化过程中有什么不同之处吗?
s=4n
两个变量
两个变量
对于n的每一个值,s都有唯一的值与它对应.
对于变量x的每一个值,变量y与之对应的值并不唯一.
金额与油量
两个变量
对于油量的每一个值,金额都有唯一的值与它对应.
进一步的研究,由“唯一”深入……
新中国成立以来,我国已经进行了六次人口普查. 下表是我国六次人口普查的人口数统计表.
年份
人口数(亿)
1953
6.02
1964
7.23
1982
10.32
1990
11.60
2000
12.95
2010
13.71
(1)在这一变化过程中,有几个变量?分别是什么?
(2)在这一变化过程中,两个变量之间有什么关系?
随着 的变化而变化.
人口数
年份
对于 的每一个值, 都有唯一的值与它对应.
年份
人口数
饭后铺在桌上的一张旧报纸引起了小薇的注意……
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
下图是苏州冬季一天的气温变化曲线.
随着 的变化而变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于 的每一个值, 都有唯一的值与它对应.
在这一变化过程中,两个变量之间有什么关系?
温度
时间
时间
温度
?
?
?
同学们,你们能从刚才的几个变化过程中找到它们的共同之处吗?
对于 的每一个值,
有_____值与之对应.
S=4n
相信你能发现
金额与油量
两
唯一
随之变化
人口数与年份
温度T与时间t
每个变化过程中都有___个变量,
其中 变化时,
也___________;
x 和 y
x
y
x
y
一个变量
另一个变量
其中一个变量
另一个变量
其中,x是自变量, y是因变量.
一般地, 在一个变化过程中的两个变量x和y,如果对于x的每一个值, y都有唯一的值与它对应,那么我们称y是x的函数.
相信你能理解
函数小史
function
莱布尼兹
(德国)
李善兰
(清代)
凡此变数函彼变数,则此为彼之函数 .
(这里的“函”有包含的意思.)
函数
翻译
S =4n
金额与油量
金额是油量的函数吗?
想一想
s是n的函数吗?
年份
人口数(亿)
1953
6.02
1964
7.23
1982
10.32
1990
11.60
2000
12.95
2010
13.71
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
人口数是年份的函数吗?
温度T是时间t的函数吗?
中,y是x的函数吗?
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
解析法
列表法
图像法
函数的三种表示方法
S =4n
年份
人口数(亿)
1953
6.02
1964
7.23
1982
10.32
1990
11.60
2000
12.95
2010
13.71
(函数解析式)
舅舅说最近村子里有黄鼠狼,小薇准备帮助舅舅用一段20m长的栅栏围一个长方形鸡舍……
(1)当长方形的宽为2m时,长为 ____ m;
(2)当长方形的宽为4m时,长为 ____ m;
(3)当长方形的宽为b m时,长为 ______ m.
8
6
(10-b)
(4)长方形的长是宽的函数吗?为什么?
帮舅舅围鸡舍……
(5)长方形的宽是长的函数吗?为什么?
(6)长方形的面积是宽的函数吗?为什么?
我们的探索和研究也接近尾声,
下面就请同学们运用函数的概念
来解决几个小问题.
忙碌中,小薇假期的一天结束了
1.下列表格反映了一个变化过程中y与x的关系,其中y 是x的函数吗?
(2)
(1)
练一练
2.在平行四边形面积公式 (a表示平行四边形的底,h表示底边上的高),若a固定,h是自变量,则a是____量,而面积S是____的函数;若h固定,a是自变量,则常量是____,而面积S是____的函数;
常
h
h
a
练一练
若S 固定,则常量是____,____是____的函数
3.(1)若每吨民用自来水的价格为2.8元,所交水 费金额为y(元),使用自来水的数量为x(吨),
则 y 是 x 的函数吗?为什么?
(2)底边为6(m)的三角形面积为s(㎡),高为h (m), s是h的函数吗?为什么?
练一练
?
?
4.根据小鱼的条数与所需火柴棒的根数的关系,
说说你从中获得的信息.
6n+2
s=6n+2
……
……
8
14
20
n
火柴的根数(s)
小鱼条数(n)
2
1
3
……
……
练一练
5.为了加强居民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水x吨(x>10),应交水费y元.请求出y和x的表达式,并判断y是否为x的函数.
练一练
y =12+1.8(x-10)
=1.8x-6
6.用60m的篱笆围成长方形,使长方形一边靠墙
(墙足够长),另三边用篱笆围成
墙
a
a
b
(3)写出长方形面积s(m2)与平行于墙的一边长
b(m)的关系式;
(4)并指出上式中的函数与自变量.
(1)写出长方形面积s(m2)与垂直于墙的一边长
a(m)的关系式;
(2)指出上式中的函数与自变量.
练一练
小结
2.函数:
1.常量和变量:
在某一变化过程中,数值保持不变的量叫做常量;
可以取不同数值的量叫做变量.
一般地,设在一个变化的过程中有两个变量x和y,
并且对于变量x的每一个值,变量y都有唯一的值
与它对应,那么我们称y是x的函数(function).
其中,x是自变量,y是因变量.
自己找一个实际生活中表示函数关系例子.
小组交流的要求:
每个人轮流说说自己编的函数实例,推荐一名同学准备班级交流.
相信你能应用
时间是一个“变量”,愿你们在飞驰而去的时间波涛上,乘风破浪,驶向成功的彼岸;
人生也是个“变量”,愿你们在前行的道路上,用自己的双手建造幸运的大厦。
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
