3.3 指数和指数函数习题课 课件(33张ppt)
文档属性
| 名称 | 3.3 指数和指数函数习题课 课件(33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 476.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 09:17:33 | ||
图片预览











文档简介
指数和指数函数
习题课
1.化简:(式中的字母均是正数)
习题讲解
(1)
(2)
2.计算下列各式的值:
(1) (2)
习题讲解
问题1 进行指数运算时的运算依据是什么?在运算时需要注意什么?
进行指数运算的运算依据是实数指数幂的运算性质.在运算时,要尽量把根式写成指数幂的形式,并注意 与 的区别.
1.化简:(式中的字母均是正数)
习题讲解
(1)
(2)
解:(1)
1.化简:(式中的字母均是正数)
习题讲解
(1)
(2)
解:(2)
习题讲解
2.计算下列各式的值:
(1) (2)
解:(1)
(2)
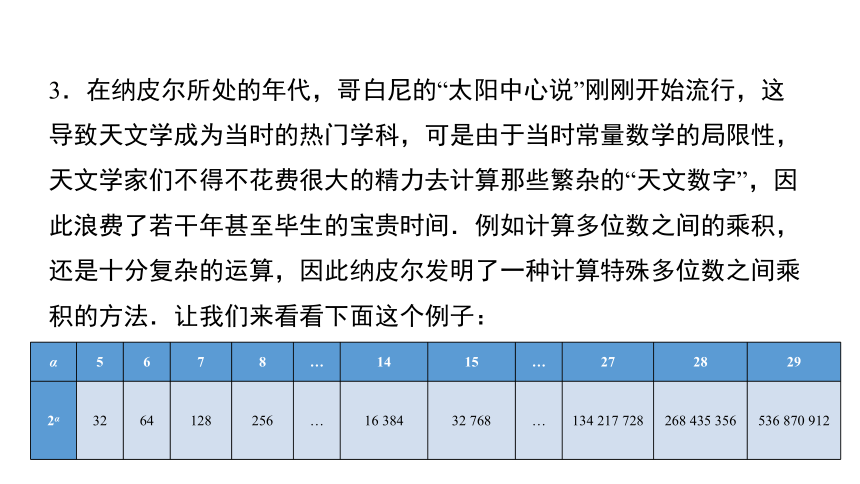
3.在纳皮尔所处的年代,哥白尼的“太阳中心说”刚刚开始流行,这导致天文学成为当时的热门学科,可是由于当时常量数学的局限性,天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵时间.例如计算多位数之间的乘积,还是十分复杂的运算,因此纳皮尔发明了一种计算特殊多位数之间乘积的方法.让我们来看看下面这个例子:
习题讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}α
5
6
7
8
…
14
15
…
27
28
29
2α
32
64
128
256
…
16 384
32 768
…
134 217 728
268 435 356
536 870 912
这两行数字之间的关系是极为明确的:第一行表示2的指数,第二行表示2的对应幂.如果我们要计算第二行中两个数的乘积,可以通过第一行对应数字的和来实现.比如计算64×256的值,就可以先查第一行的对应数字:64对应6,256对应8,然后再把第一行中的对应数字加起来6+8=14;第一行中的14,对应第二行中的16 384,所以有64×256=16 384.
习题讲解
按照这样的方法计算16 384×32 768=____________.
4.已知 ,则 ____________.
习题讲解
问题2 指数运算中,对于同底数指数幂的乘除运算,反映在指数上有什么特点?由此可知,同底数指数幂的乘法运算,如果指数互为相反数,那么运算结果是什么?
同底数指数幂的乘除运算,反映在指数上为指数的相加减,这样就由二级运算乘除法,变成了一级运算加减法.特别地,如果同底数指数幂相乘,指数互为相反数,那么运算结果为该底数的0次幂,即结果为1.
习题讲解
3.按照这样的方法计算16 384×32 768=____________.
解:16 384对应14,32 768对应15,而14+15=29,查表可得第一行中的29对应第二行中的536 870 912,所以16 384×32 768=536 870 912.
536 870 912
习题讲解
4.已知 ,则 ____________.
解:由 ,可得 .
由 ,可得 .
所以 ,则
-4
5.若函数 是指数函数,则a的值是__________.
习题讲解
6.某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为__________.
习题讲解
问题3 判断一个函数是否为指数函数的依据是什么?什么是指数型函数?怎样判断指数型函数是增长的还是衰减的?
判断依据是指数函数解析式的特征:①底数a>0且a≠1;②ax的系数为1;③自变量x的系数为1.形如y=kax的函数为指数型函数,其中k为常数.一般当k>0时,若a>1,则刻画指数增长变化规律,若0<a<1,则刻画指数衰减变化规律.
5.若函数 是指数函数,则a的值是__________.
习题讲解
解得a=1(舍)或a=3.所以a=3.
解:因为 是指数函数,所以 ,
3
6.某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为__________.
习题讲解
当t=1时,y=20,所以20=10ek,即ek=2.
解:由题意可知,初始时有10个细菌,
1280
所以y=10·2t,若t=7,则可得此时的细菌数为y=10·2t =1280.
7.若函数 (a>0且a≠1)的图象恒过点 ,则m+n=____________.
习题讲解
8.函数 (a>1)的图象的大致形状是( )
A B C D
9.已知a=0.80.7,b=0.80.9 ,c=1.20.8,则a,b,c的大小关系是( )
习题讲解
A.b>a>c B.c>a>b
C.c>b>a D.a>b>c
习题讲解
问题4 我们在研究指数函数的图象和性质时,研究了它的哪些性质?
我们研究了指数函数的定义域、值域、单调性,并且还发现了指数函数恒过定点(0,1).
7.若函数 (a>0且a≠1)的图象恒过点 ,则m+n=____________.
习题讲解
解:由于指数函数 (a>0且a≠1)的图象恒过定点 ,所以
(a>0且a≠1)的图象可以看成是由指数函数
的图象先向左平移m个单位变成 ,此时的图象恒过点
然后再纵向拉伸2倍变成 ,此时的图象恒过点 .最后再向下平移n个单位变成 ,此时的图象恒过点
由于 的图象恒过点 ,所以m=1,n=-2.
7.若函数 (a>0且a≠1)的图象恒过点 ,则m+n=____________.
习题讲解
也可以考虑,指数函数 (a>0且a≠1)之所以恒过定点 ,
是因为对于任意的a>0且a≠1,都有 .所以对于函数
,令 ,可得 ,即该函数恒过
点 ,所以m=1,n=-2.
因此m+n=-1.
-1
习题讲解
8.函数 (a>1)的图象的大致形状是( )
A B C D
所以根据指数函数的图象性质,选C.
解:易知 ,且a>1,
C
9.已知a=0.80.7,b=0.80.9 ,c=1.20.8,则a,b,c的大小关系是( )
习题讲解
A.b>a>c B.c>a>b
C.c>b>a D.a>b>c
解:因为指数函数 在其定义域上是减函数,
所以 ,即a>b.
又因为 , ,所以c>a.
综上有c>a>b,选B.
B
10.求函数 的单调递增区间.
习题讲解
11.函数 的值域为____________.
12.若函数 (a>0且a≠1),满足 ,则 的单调递减区间是____________.
习题讲解
问题5 在求解与指数函数相关的复合函数的问题时,应当注意什么?可以用什么样的方法,让问题的讨论变得简化?
需要充分考虑指数函数的定义域、值域、单调性,并且还要注意多个函数复合以后,所带来的定义域、值域、单调性的改变.可以采取换元的方法,将复合函数看成是指数函数与其它简单函数的复合,分层逐次讨论各个函数的性质.
10.求函数 的单调递增区间.
习题讲解
解:令 ,则 .
因为 ,可得t的增区间为 .
因为函数 在R上是增函数,
所以函数 的单调递增区间为 .
习题讲解
解:令 ,则 .
因为 ,可得t的值域为 .
因为函数 在R上是减函数,
11.函数 的值域为____________.
当t=1时, ,所以函数 的值域为 .
习题讲解
解:由 ,得 ,
所以 ,即 .
因为 在R上是减函数,
所以只需考虑 的单调递增区间,
12.若函数 (a>0且a≠1),满足 ,则 的单调递减区间是____________.
令 ,则 .
易知其单调递增区间为 .
习题讲解
解:所以函数 的单调递减区间是 .
12.若函数 (a>0且a≠1),满足 ,则 的单调递减区间是____________.
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
的使用条件为 .例如 ,此时底数 ,如果利用该性质得到 ,这显然是错误的.
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
的使用条件为 .例如
,此时底数 ,如果利用该性质得到
,这显然是错误的.
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
指数函数的解析式的特征为:①底数a>0且a≠1;②ax的系数为1;③自变量x的系数为1.即 (a>0且a≠1).
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
在解与指数函数相关的问题时,要注意其底数、值域都有特定的取值范围,即底数a>0且a≠1,值域为 .并且还要注意指数函数为单调函数,当0<a<1是为减函数,当a>1时为增函数,并且恒过定点(0,1).
再见
习题课
1.化简:(式中的字母均是正数)
习题讲解
(1)
(2)
2.计算下列各式的值:
(1) (2)
习题讲解
问题1 进行指数运算时的运算依据是什么?在运算时需要注意什么?
进行指数运算的运算依据是实数指数幂的运算性质.在运算时,要尽量把根式写成指数幂的形式,并注意 与 的区别.
1.化简:(式中的字母均是正数)
习题讲解
(1)
(2)
解:(1)
1.化简:(式中的字母均是正数)
习题讲解
(1)
(2)
解:(2)
习题讲解
2.计算下列各式的值:
(1) (2)
解:(1)
(2)
3.在纳皮尔所处的年代,哥白尼的“太阳中心说”刚刚开始流行,这导致天文学成为当时的热门学科,可是由于当时常量数学的局限性,天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵时间.例如计算多位数之间的乘积,还是十分复杂的运算,因此纳皮尔发明了一种计算特殊多位数之间乘积的方法.让我们来看看下面这个例子:
习题讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}α
5
6
7
8
…
14
15
…
27
28
29
2α
32
64
128
256
…
16 384
32 768
…
134 217 728
268 435 356
536 870 912
这两行数字之间的关系是极为明确的:第一行表示2的指数,第二行表示2的对应幂.如果我们要计算第二行中两个数的乘积,可以通过第一行对应数字的和来实现.比如计算64×256的值,就可以先查第一行的对应数字:64对应6,256对应8,然后再把第一行中的对应数字加起来6+8=14;第一行中的14,对应第二行中的16 384,所以有64×256=16 384.
习题讲解
按照这样的方法计算16 384×32 768=____________.
4.已知 ,则 ____________.
习题讲解
问题2 指数运算中,对于同底数指数幂的乘除运算,反映在指数上有什么特点?由此可知,同底数指数幂的乘法运算,如果指数互为相反数,那么运算结果是什么?
同底数指数幂的乘除运算,反映在指数上为指数的相加减,这样就由二级运算乘除法,变成了一级运算加减法.特别地,如果同底数指数幂相乘,指数互为相反数,那么运算结果为该底数的0次幂,即结果为1.
习题讲解
3.按照这样的方法计算16 384×32 768=____________.
解:16 384对应14,32 768对应15,而14+15=29,查表可得第一行中的29对应第二行中的536 870 912,所以16 384×32 768=536 870 912.
536 870 912
习题讲解
4.已知 ,则 ____________.
解:由 ,可得 .
由 ,可得 .
所以 ,则
-4
5.若函数 是指数函数,则a的值是__________.
习题讲解
6.某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为__________.
习题讲解
问题3 判断一个函数是否为指数函数的依据是什么?什么是指数型函数?怎样判断指数型函数是增长的还是衰减的?
判断依据是指数函数解析式的特征:①底数a>0且a≠1;②ax的系数为1;③自变量x的系数为1.形如y=kax的函数为指数型函数,其中k为常数.一般当k>0时,若a>1,则刻画指数增长变化规律,若0<a<1,则刻画指数衰减变化规律.
5.若函数 是指数函数,则a的值是__________.
习题讲解
解得a=1(舍)或a=3.所以a=3.
解:因为 是指数函数,所以 ,
3
6.某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为__________.
习题讲解
当t=1时,y=20,所以20=10ek,即ek=2.
解:由题意可知,初始时有10个细菌,
1280
所以y=10·2t,若t=7,则可得此时的细菌数为y=10·2t =1280.
7.若函数 (a>0且a≠1)的图象恒过点 ,则m+n=____________.
习题讲解
8.函数 (a>1)的图象的大致形状是( )
A B C D
9.已知a=0.80.7,b=0.80.9 ,c=1.20.8,则a,b,c的大小关系是( )
习题讲解
A.b>a>c B.c>a>b
C.c>b>a D.a>b>c
习题讲解
问题4 我们在研究指数函数的图象和性质时,研究了它的哪些性质?
我们研究了指数函数的定义域、值域、单调性,并且还发现了指数函数恒过定点(0,1).
7.若函数 (a>0且a≠1)的图象恒过点 ,则m+n=____________.
习题讲解
解:由于指数函数 (a>0且a≠1)的图象恒过定点 ,所以
(a>0且a≠1)的图象可以看成是由指数函数
的图象先向左平移m个单位变成 ,此时的图象恒过点
然后再纵向拉伸2倍变成 ,此时的图象恒过点 .最后再向下平移n个单位变成 ,此时的图象恒过点
由于 的图象恒过点 ,所以m=1,n=-2.
7.若函数 (a>0且a≠1)的图象恒过点 ,则m+n=____________.
习题讲解
也可以考虑,指数函数 (a>0且a≠1)之所以恒过定点 ,
是因为对于任意的a>0且a≠1,都有 .所以对于函数
,令 ,可得 ,即该函数恒过
点 ,所以m=1,n=-2.
因此m+n=-1.
-1
习题讲解
8.函数 (a>1)的图象的大致形状是( )
A B C D
所以根据指数函数的图象性质,选C.
解:易知 ,且a>1,
C
9.已知a=0.80.7,b=0.80.9 ,c=1.20.8,则a,b,c的大小关系是( )
习题讲解
A.b>a>c B.c>a>b
C.c>b>a D.a>b>c
解:因为指数函数 在其定义域上是减函数,
所以 ,即a>b.
又因为 , ,所以c>a.
综上有c>a>b,选B.
B
10.求函数 的单调递增区间.
习题讲解
11.函数 的值域为____________.
12.若函数 (a>0且a≠1),满足 ,则 的单调递减区间是____________.
习题讲解
问题5 在求解与指数函数相关的复合函数的问题时,应当注意什么?可以用什么样的方法,让问题的讨论变得简化?
需要充分考虑指数函数的定义域、值域、单调性,并且还要注意多个函数复合以后,所带来的定义域、值域、单调性的改变.可以采取换元的方法,将复合函数看成是指数函数与其它简单函数的复合,分层逐次讨论各个函数的性质.
10.求函数 的单调递增区间.
习题讲解
解:令 ,则 .
因为 ,可得t的增区间为 .
因为函数 在R上是增函数,
所以函数 的单调递增区间为 .
习题讲解
解:令 ,则 .
因为 ,可得t的值域为 .
因为函数 在R上是减函数,
11.函数 的值域为____________.
当t=1时, ,所以函数 的值域为 .
习题讲解
解:由 ,得 ,
所以 ,即 .
因为 在R上是减函数,
所以只需考虑 的单调递增区间,
12.若函数 (a>0且a≠1),满足 ,则 的单调递减区间是____________.
令 ,则 .
易知其单调递增区间为 .
习题讲解
解:所以函数 的单调递减区间是 .
12.若函数 (a>0且a≠1),满足 ,则 的单调递减区间是____________.
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
的使用条件为 .例如 ,此时底数 ,如果利用该性质得到 ,这显然是错误的.
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
的使用条件为 .例如
,此时底数 ,如果利用该性质得到
,这显然是错误的.
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
指数函数的解析式的特征为:①底数a>0且a≠1;②ax的系数为1;③自变量x的系数为1.即 (a>0且a≠1).
归纳小结
问题6 在运用实数指数幂的运算性质 和
时,要注意什么?你能举个例子来说明吗?指数函数的解析式有什么特征?在解与指数函数相关的问题时,需要注意什么?
在解与指数函数相关的问题时,要注意其底数、值域都有特定的取值范围,即底数a>0且a≠1,值域为 .并且还要注意指数函数为单调函数,当0<a<1是为减函数,当a>1时为增函数,并且恒过定点(0,1).
再见
同课章节目录
