2020年秋苏科版九年级数学上册随堂练——2.7弧长及扇形的面积提升练习(word版,含答案)
文档属性
| 名称 | 2020年秋苏科版九年级数学上册随堂练——2.7弧长及扇形的面积提升练习(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览


文档简介
2.7弧长及扇形的面积提升练习
一、选择题
1.一个扇形的半径为8cm,弧长为
cm,则扇形的圆心角为(??
)
A.?60°?????????????????????????????????????B.?120°???????????????????????????????????
C.?150°???????????????????????????????????D.?180°
2.在半径为1的⊙O中,120°的圆心角所对的弧长是
()
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为(
)
A.10π
B.
C.
D.π
4.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为(?
)
A.??????????????????????????????????B.?2π???????????????????????????????????????C.?3π?????????????????????????????????????D.?12π
5.如图,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是(
)
A.2π
cm
B.4π
cm
C.8π
cm
D.16π
cm
6.如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )
A.2-
B.2-
C.4-
D.4-
7.如图,一根5m长的绳子,一端拴在互相垂直的围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是(
)
A.
m2
B.
m2
C.
m2
D.
m2
8.若扇形的圆心角为90°,半径为6,则该扇形的弧长为(
??)
A.???????????????????????????????????????B.??????????????????????????????????????
C.???????????????????????????????????????D.?
9.挂钟分针的长10cm,经过20分钟,它的针尖转过的路程是(?????
)
A.?cm??????????????????????????????B.?cm???????????????????????????????C.?cm????????????????????????????D.?cm
二、填空题
10.一个扇形的弧长是π
cm,半径是6
cm,则此扇形的圆心角是________度.
11.如图
,在边长为4的正方形ABCD中,以点B为圆心,以AB长为半径画弧,交对角线BD于点E,则图中阴影部分的面积是________(结果保留π).
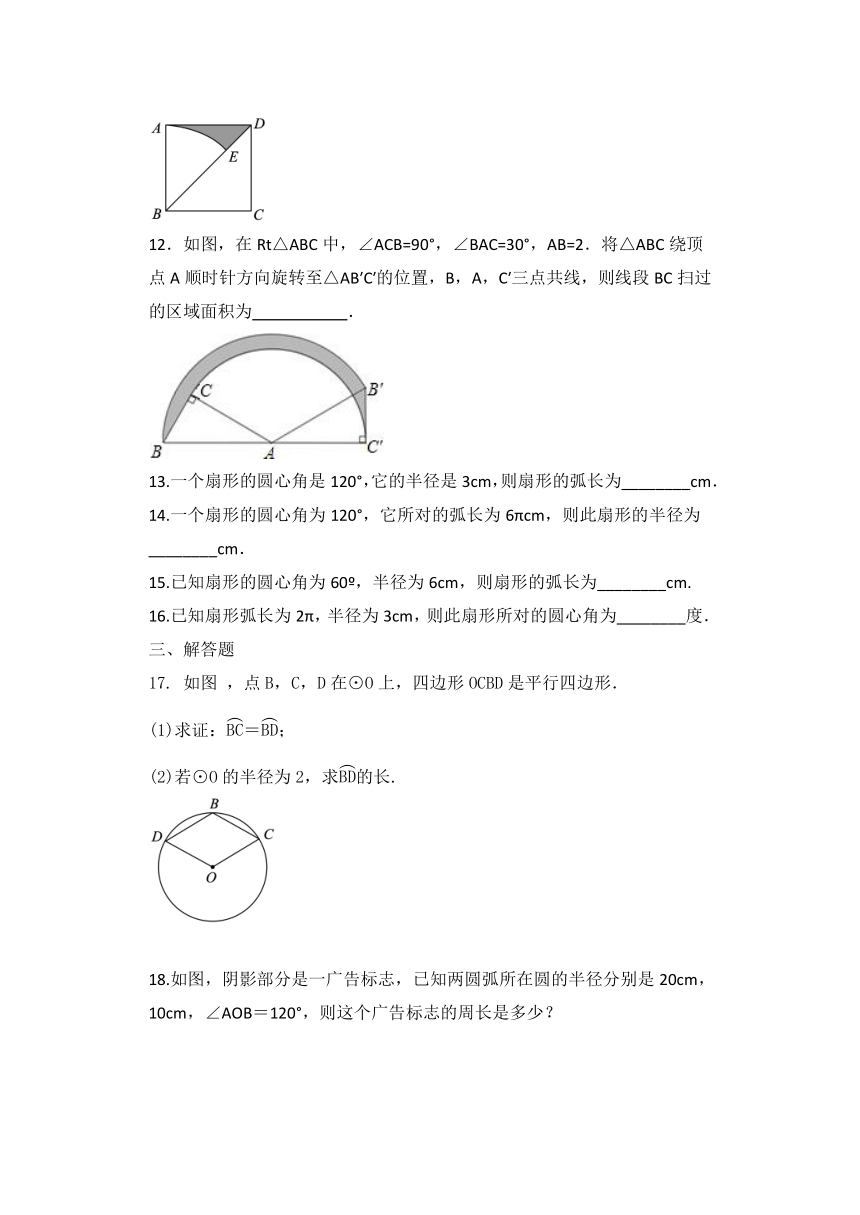
12.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为
.
13.一个扇形的圆心角是120°,它的半径是3cm,则扇形的弧长为________cm.
14.一个扇形的圆心角为120°,它所对的弧长为6πcm,则此扇形的半径为________cm.
15.已知扇形的圆心角为60?,半径为6cm,则扇形的弧长为________cm.
16.已知扇形弧长为2π,半径为3cm,则此扇形所对的圆心角为________度.
三、解答题
17.
如图
,点B,C,D在⊙O上,四边形OCBD是平行四边形.
(1)求证:=;
(2)若⊙O的半径为2,求的长.
18.如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
19.方程思想如图
所示,在△ABC中,∠C=90°,AC+BC=9,O是斜边AB上一点,以点O为圆心,2为半径的圆分别与AC,BC相切于点D,E.
(1)求AC,BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(π取3.14).
答案
1.
B
2.
B
3.
C
4.
C
5.
B
6.
A
7.
D
8.
C
9.
A
10.
36
11.
8-2π
12.
13.
14.
9
15.
16.
120
17.
解:(1)证明:如图,连接OB.
∵四边形OCBD是平行四边形,
∴OC=BD,OD=BC,
而OC=OD,
∴BD=BC,
∴=.
(2)由(1)知OD=OB=OC=BD=BC,
∴△OBD和△OBC均为等边三角形,
∴∠BOC=∠BOD=60°,
∴的长为=π.
18.
解:
,AC=BD=20-10=10cm,
∴周长=(
)cm
19.
解:(1)如图,连接OD,OC,OE.
∵D,E为⊙O的切点,
∴OD⊥AC,OE⊥BC,OD=OE=2.
∵S△ABC=S△AOC+S△BOC,AC+BC=9,
∴AC·BC=AC·OD+BC·OE,
∴AC×2+BC×2=AC+BC=9,
即AC·BC=18.
又∵AC+BC=9,
∴AC,BC的长是方程x2-9x+18=0的两个根,
解得x=3或x=6.
∴AC=3,BC=6或AC=6,BC=3.
(2)如图,连接DE,则S阴影=S△BDE+S扇形ODE-S△ODE.
∵AC=3,∴BC=6.
∵OD⊥AC,OE⊥BC,∠ACB=90°,OD=OE,
∴四边形OECD是正方形,
∴EC=OE=2,
∴BE=BC-EC=6-2=4,
∴S△BDE=BE·DC=×4×2=4,S扇形ODE=π×22=π,S△ODE=OD·OE=2,
∴S阴影=4+π-2=2+π≈5.14.
一、选择题
1.一个扇形的半径为8cm,弧长为
cm,则扇形的圆心角为(??
)
A.?60°?????????????????????????????????????B.?120°???????????????????????????????????
C.?150°???????????????????????????????????D.?180°
2.在半径为1的⊙O中,120°的圆心角所对的弧长是
()
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为(
)
A.10π
B.
C.
D.π
4.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为(?
)
A.??????????????????????????????????B.?2π???????????????????????????????????????C.?3π?????????????????????????????????????D.?12π
5.如图,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是(
)
A.2π
cm
B.4π
cm
C.8π
cm
D.16π
cm
6.如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )
A.2-
B.2-
C.4-
D.4-
7.如图,一根5m长的绳子,一端拴在互相垂直的围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是(
)
A.
m2
B.
m2
C.
m2
D.
m2
8.若扇形的圆心角为90°,半径为6,则该扇形的弧长为(
??)
A.???????????????????????????????????????B.??????????????????????????????????????
C.???????????????????????????????????????D.?
9.挂钟分针的长10cm,经过20分钟,它的针尖转过的路程是(?????
)
A.?cm??????????????????????????????B.?cm???????????????????????????????C.?cm????????????????????????????D.?cm
二、填空题
10.一个扇形的弧长是π
cm,半径是6
cm,则此扇形的圆心角是________度.
11.如图
,在边长为4的正方形ABCD中,以点B为圆心,以AB长为半径画弧,交对角线BD于点E,则图中阴影部分的面积是________(结果保留π).
12.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为
.
13.一个扇形的圆心角是120°,它的半径是3cm,则扇形的弧长为________cm.
14.一个扇形的圆心角为120°,它所对的弧长为6πcm,则此扇形的半径为________cm.
15.已知扇形的圆心角为60?,半径为6cm,则扇形的弧长为________cm.
16.已知扇形弧长为2π,半径为3cm,则此扇形所对的圆心角为________度.
三、解答题
17.
如图
,点B,C,D在⊙O上,四边形OCBD是平行四边形.
(1)求证:=;
(2)若⊙O的半径为2,求的长.
18.如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
19.方程思想如图
所示,在△ABC中,∠C=90°,AC+BC=9,O是斜边AB上一点,以点O为圆心,2为半径的圆分别与AC,BC相切于点D,E.
(1)求AC,BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(π取3.14).
答案
1.
B
2.
B
3.
C
4.
C
5.
B
6.
A
7.
D
8.
C
9.
A
10.
36
11.
8-2π
12.
13.
14.
9
15.
16.
120
17.
解:(1)证明:如图,连接OB.
∵四边形OCBD是平行四边形,
∴OC=BD,OD=BC,
而OC=OD,
∴BD=BC,
∴=.
(2)由(1)知OD=OB=OC=BD=BC,
∴△OBD和△OBC均为等边三角形,
∴∠BOC=∠BOD=60°,
∴的长为=π.
18.
解:
,AC=BD=20-10=10cm,
∴周长=(
)cm
19.
解:(1)如图,连接OD,OC,OE.
∵D,E为⊙O的切点,
∴OD⊥AC,OE⊥BC,OD=OE=2.
∵S△ABC=S△AOC+S△BOC,AC+BC=9,
∴AC·BC=AC·OD+BC·OE,
∴AC×2+BC×2=AC+BC=9,
即AC·BC=18.
又∵AC+BC=9,
∴AC,BC的长是方程x2-9x+18=0的两个根,
解得x=3或x=6.
∴AC=3,BC=6或AC=6,BC=3.
(2)如图,连接DE,则S阴影=S△BDE+S扇形ODE-S△ODE.
∵AC=3,∴BC=6.
∵OD⊥AC,OE⊥BC,∠ACB=90°,OD=OE,
∴四边形OECD是正方形,
∴EC=OE=2,
∴BE=BC-EC=6-2=4,
∴S△BDE=BE·DC=×4×2=4,S扇形ODE=π×22=π,S△ODE=OD·OE=2,
∴S阴影=4+π-2=2+π≈5.14.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
