苏科版七年级上册数学 2.5有理数的加法与减法课件(共54张PPT)
文档属性
| 名称 | 苏科版七年级上册数学 2.5有理数的加法与减法课件(共54张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 10:01:07 | ||
图片预览










文档简介
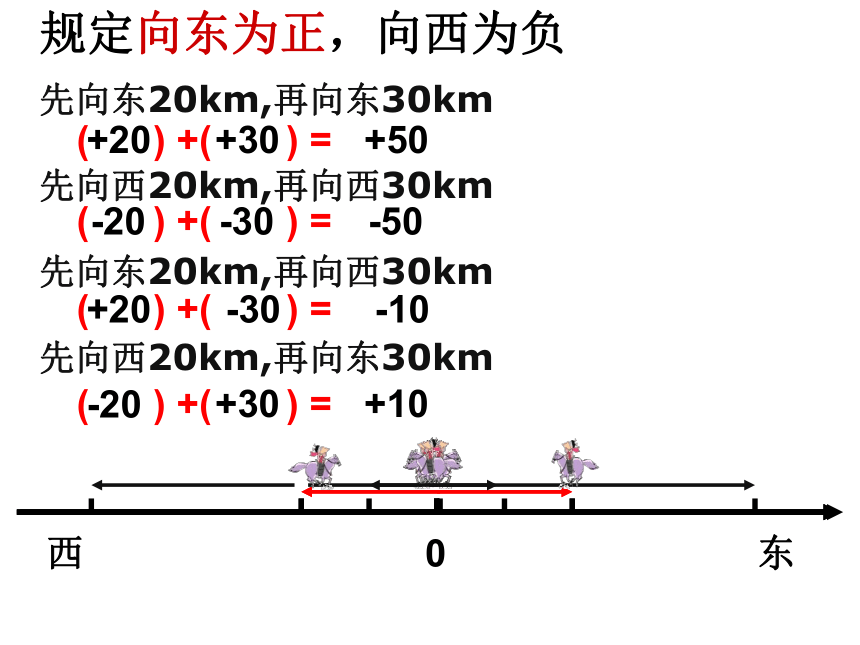
小明骑马行驶在东西方向大道上,先走了20km,又走了30km, 此时你能确定小明的位置吗?
你能将所有的情况设想完整吗?
先向东20km,再向东30km
先向西20km,再向西30km
先向东20km,再向西30km
先向西20km,再向东30km
规定向东为正,向西为负
+20
+30
+50
-20
-30
-50
+20
-30
-10
-20
+30
+10
( ) +( ) =
( ) +( ) =
( ) +( ) =
( ) +( ) =
东
西
0
这四个算式跟小学时的算式有什么不一样?
+20
+30
+50
( ) +( ) =
-20
-30
-50
( ) +( ) =
+20
-30
-10
( ) +( ) =
-20
+30
+10
( ) +( ) =
+20
+30
+50
( ) +( ) =
-20
-30
-50
( ) +( ) =
+20
-30
-10
( ) +( ) =
-20
+30
+10
( ) +( ) =
两个有理数相加,和的符号怎样确定?和的绝
对值怎样确定?
同号两数相加,,取相同的符号,并把绝对值相加;
异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(1)(-3)+3 = ?
(2) 5+(-5)= ?
(3)(-3)+0 = ?
(4) 0 +3 = ?
有理数加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)异号两数相加,
绝对值相等时,和为0;
绝对值不等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)一个数与0相加,仍得这个数.
例
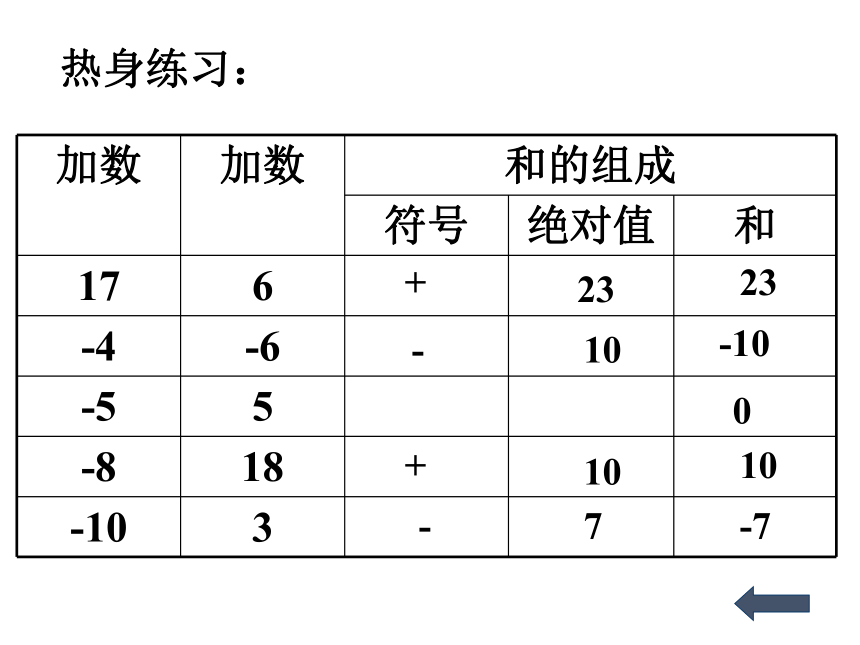
加数
加数
和的组成
符号
绝对值
和
17
6
-4
-6
-5
5
-8
18
-10
3
热身练习:
0
+
+
-
-
23
23
10
10
10
-10
7
-7
例1、计算:
(1)(-15)+(-3) (2)(-180)+(+20)
(3)5+(-25)
(4)5+(-5) (5)0+(-2)
(1)选择运算法则;
(2)确定和的符号(同号取同,异号取大);
(3)确定和的绝对值.
1、下列计算正确的是( )
A. (+20)+(-30) B. (-31)+(-11)
=-(30+20) =-(31-11)
=-50 =-20
C.(-3)+(+3)=0 D. (-2.5)+(+2.1)
=+(2.5-2.1)
=0.4
2、计算:P32 T1
(1)(-13)+25 (2)(52)+(-17)
(3)(-52)+(-7) (4)(-23)+0
(5)(-4.5)+4.5
(6) (7)
2、在括号内填上适当的数,使等式成立:
(1)( )+(-5)= 0
(2)( )+(-5)=-8
(3)(-5)+( )=-1
(4)(-5)+( )= 9
3
某商场经理对今年上半年每月的利润作了如下记录:1,2,5,6月盈利分别是13万元,12万元,12.5万元,10万元,3,4亏损分别是0.7万元和0.8万元。试用正负数表示各月的利润,并算出该商场上半年的总利润.
2.5有理数的加法与减法(二)
1、有理数加法法则是什么?
2、进行有理数加法运算的一般步骤什么?
问题: 你知道该如何计算吗?
问题:引入负数后,加法的交换律和结合律还成立吗?
情景1:
3
﹢
-5
﹦
_
-2
-5
3
﹢
﹦
_
-2
活动1:
你们能再举一些数字也符合这样的结论吗?试试看!
情景2:
3
-5
﹢
﹦
_
)
-7
-9
(
﹢
3
-5
﹢
﹢
﹦
_
-7
-9
(
)
活动2:
你们能再举一些数字也符合这样的结论吗?试试看!
规律探究:相信你能行!
加法的交换律:
a+b=b+a
加法的结合律:
(a+b)+c=a+(b+c)
总结提
加法的交换律:a+b=b+a
加法的结合律:(a+b)+c=a+(b+c)
交换律改变
加数的前后位置
结合律改变
运算的前后顺序
计算:
(1)(-23)+(+58)+(-17)
(2)(-2.8)+(-3.6)+(-1.5)+3.6
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
符号相同的先结合
互为相反数的先结合
分母相同的先结合
相加得整的结合
(4)(+4.56)+(-3.45)+(+4.44)+2.45
巩固
计算
(1) (-11)+8+(-14)
(2)(- —)+ (- —) + (- —) + —
(3)0.35+(-0.6)+0.25+(-5.4)
3
4
2
3
4
1
3
2
简便运算可以从以下几方面考虑:
(1) 相反数结合法:互为相反数的两个数先相加
(2) 凑整法:几个数相加得到整数,先相加
(3) 同分母结合法:分母相同的数先相加
(4) 同号结合法:符号相同的两个数相加
(5) 同型结合法:整数与整数,小数与小数相加
注:有时需先统一成分数或小数
比一比看谁算得好
计算:
(4) 8+(-2)+(-4)+1+(-3)
巩固
考考你自己!
1. 计算: (-5)+9+(-6)+7 = ____
2. 绝对值小于5的所有整数的和为_ _ ____
3. 在括号里填写每步运算的根据:
(-8)+(-5)+8
=(-8)+8+(-5) ( )
=〔(-8)+8〕+(-5) ( )
=0+(-5) ( )
=-5 ( )
加法交换律
加法结合律
互为相反数的两数之和为0
0与任何数相加仍得这个数
5
0
能力提升
计算:
4 . -1+2+(-3)+4+ …+2015+(-2016)
拓展
5. 小虫从某点O出发,在一直线上来回爬行,假定向右爬行记为正数,向左爬行记为负数,爬行的过程依次为(单位:厘米):
+5, -3,+10, -8, -6, +12, -13.
试问:(1)小虫最后能否回到出发点O?
(2)若不在点O,小虫在哪里?
(3)小虫爬行的总路程是多少?
1、(+2)+( )=+1
试一试:
2、(-3)+( )= -10
3、( )+ ( -5 )= 1.5
4、( )+( + )= 1.5
5、(+0.1 )+( )= 0
6、 +( )= 2
1.使用加法运算律, 可使运算简便.
课堂小结:
1.你对你自己的表现如何?
2.你对同桌的的学习表现如何?
3.通过这节课的学习,你有什么收获?
体会:
2.培养了概括力和符号感.
5 - (-3) = _____?
一天中的最高气温与最低气温的差叫做日温差.
如果某天最高气温是5℃,最低气温是-3℃,
那么这天的日温差是_____.
8℃
小学里学过减法是加法的逆运算.因为8+(-3)=5,所以5-(-3)=8.
加法
减法
从上往下看,从5℃到-3℃,温度下降了5+3=8℃
于是得到 5-(-3)= 5+3
5 -(-3) = 8
5 + 3 = 8
减号变为加号
-3变成它的相反数3
总 结
有理数减法法则
减去一个数,等于加上这个数的相反数.
【试一试】
填空:
(1)(-3)-5 = (-3)+____
(2) 3-(-5) = 3+____
(-5)
5
(3) 3-5 = 3+____
(-5)
(4) (-3)-(-5) =(-3)+____
5
【例题精讲】
例1、计算
(2) 8.5-(-1.5)
(1) 0-(-22)
(4)
(3) (+4)-16
练习1:
(1) 3 – 5 ; (2) 3 – ( – 5);
(3)( – 3)– 5; (4)(– 3) –( –5);
(5)( – 6)– 6; (6) 6-(-6) ;
(7) (–6)–(–6) ; (8)– 7 – 0 .
例2、根据天气
预报图, 计算
右图中各城市
的日温差.
【例题精讲】
分别输入0,1,-1,按图所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行计算).并写出输出的结果.
输入
+4
-(-3)
-5
>2
输出
是
否
练习2:
(1)( )+(-8)=-12;
(2)(+8)+( )=-12;
(3)( )-(-7.1)=8;
(4)(-2)-( )=-7;
(5)在数轴上表示数7的点与表示-1的点之间
的距离是 ;
表示数-2的点与表示-6的点之间的距离
是 .
你能发现所得的距离与这两数的差有什么关系吗
【能力升级】
(6) 已知|a|=5,|b|=3,则a-b的值为____.
例4、计算
(1) (-20)-7-(-13)-(-16)
(2) (-3.4)+5.8-(+8.6)+12
【例题精讲】
练习3:
计算:
(1) 7-(-4)+(-5)
(2)(-21)-12+33+12-67
有理数的加法法则和减法法则
(1)5-8
计算:
(2)2+5-8
(3)14-(-12)+(-25)-17
有理数的加减混合运算可以统一成加法运算
(1)-3-5+4
(2)
例1、计算:
例如:-3+(-5)+4 可以写成 -3-5+4
在把有理数加减混合运算统一为加法的算式中,
负数前面的加号可以省略不写.
也就是 -3-5+4 表示 -3、-5与4 的和.
(1) -3-5+4
(2) -26+43-24+13-46
【例题精讲】
例2、计算:
练习:计算
(1)-21-12+33+12-67
(3)
(2)5.4-2.3+1.5-4.2
(1)(-5)-(-12)+(-7)-(+8)
(3)(-4)+9-(-7)-13
(2)
【例题精讲】
例3、计算
例4:若a=-3,b=2,c=-4,求下列各值:
(1)、a+b-c
(3)、a-b+c
(2)、
(4)、-a-b-c
【例题精讲】
【例题精讲】
例5、巡道员沿东西方向的铁路进行巡视维护.
他从住地出发,先向东行走了7km,休息之后
继续向东行走了3km;然后折返向西行走了11.5km.此时他在住地的什么方向?与住地的
距离是多少?
思考
(1)、当b>0时,a,a-b,a+b 哪个最大?哪个最小?
(2)、当b<0时,a,a-b,a+b 哪个最大?哪个最小?
你能将所有的情况设想完整吗?
先向东20km,再向东30km
先向西20km,再向西30km
先向东20km,再向西30km
先向西20km,再向东30km
规定向东为正,向西为负
+20
+30
+50
-20
-30
-50
+20
-30
-10
-20
+30
+10
( ) +( ) =
( ) +( ) =
( ) +( ) =
( ) +( ) =
东
西
0
这四个算式跟小学时的算式有什么不一样?
+20
+30
+50
( ) +( ) =
-20
-30
-50
( ) +( ) =
+20
-30
-10
( ) +( ) =
-20
+30
+10
( ) +( ) =
+20
+30
+50
( ) +( ) =
-20
-30
-50
( ) +( ) =
+20
-30
-10
( ) +( ) =
-20
+30
+10
( ) +( ) =
两个有理数相加,和的符号怎样确定?和的绝
对值怎样确定?
同号两数相加,,取相同的符号,并把绝对值相加;
异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(1)(-3)+3 = ?
(2) 5+(-5)= ?
(3)(-3)+0 = ?
(4) 0 +3 = ?
有理数加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)异号两数相加,
绝对值相等时,和为0;
绝对值不等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)一个数与0相加,仍得这个数.
例
加数
加数
和的组成
符号
绝对值
和
17
6
-4
-6
-5
5
-8
18
-10
3
热身练习:
0
+
+
-
-
23
23
10
10
10
-10
7
-7
例1、计算:
(1)(-15)+(-3) (2)(-180)+(+20)
(3)5+(-25)
(4)5+(-5) (5)0+(-2)
(1)选择运算法则;
(2)确定和的符号(同号取同,异号取大);
(3)确定和的绝对值.
1、下列计算正确的是( )
A. (+20)+(-30) B. (-31)+(-11)
=-(30+20) =-(31-11)
=-50 =-20
C.(-3)+(+3)=0 D. (-2.5)+(+2.1)
=+(2.5-2.1)
=0.4
2、计算:P32 T1
(1)(-13)+25 (2)(52)+(-17)
(3)(-52)+(-7) (4)(-23)+0
(5)(-4.5)+4.5
(6) (7)
2、在括号内填上适当的数,使等式成立:
(1)( )+(-5)= 0
(2)( )+(-5)=-8
(3)(-5)+( )=-1
(4)(-5)+( )= 9
3
某商场经理对今年上半年每月的利润作了如下记录:1,2,5,6月盈利分别是13万元,12万元,12.5万元,10万元,3,4亏损分别是0.7万元和0.8万元。试用正负数表示各月的利润,并算出该商场上半年的总利润.
2.5有理数的加法与减法(二)
1、有理数加法法则是什么?
2、进行有理数加法运算的一般步骤什么?
问题: 你知道该如何计算吗?
问题:引入负数后,加法的交换律和结合律还成立吗?
情景1:
3
﹢
-5
﹦
_
-2
-5
3
﹢
﹦
_
-2
活动1:
你们能再举一些数字也符合这样的结论吗?试试看!
情景2:
3
-5
﹢
﹦
_
)
-7
-9
(
﹢
3
-5
﹢
﹢
﹦
_
-7
-9
(
)
活动2:
你们能再举一些数字也符合这样的结论吗?试试看!
规律探究:相信你能行!
加法的交换律:
a+b=b+a
加法的结合律:
(a+b)+c=a+(b+c)
总结提
加法的交换律:a+b=b+a
加法的结合律:(a+b)+c=a+(b+c)
交换律改变
加数的前后位置
结合律改变
运算的前后顺序
计算:
(1)(-23)+(+58)+(-17)
(2)(-2.8)+(-3.6)+(-1.5)+3.6
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
符号相同的先结合
互为相反数的先结合
分母相同的先结合
相加得整的结合
(4)(+4.56)+(-3.45)+(+4.44)+2.45
巩固
计算
(1) (-11)+8+(-14)
(2)(- —)+ (- —) + (- —) + —
(3)0.35+(-0.6)+0.25+(-5.4)
3
4
2
3
4
1
3
2
简便运算可以从以下几方面考虑:
(1) 相反数结合法:互为相反数的两个数先相加
(2) 凑整法:几个数相加得到整数,先相加
(3) 同分母结合法:分母相同的数先相加
(4) 同号结合法:符号相同的两个数相加
(5) 同型结合法:整数与整数,小数与小数相加
注:有时需先统一成分数或小数
比一比看谁算得好
计算:
(4) 8+(-2)+(-4)+1+(-3)
巩固
考考你自己!
1. 计算: (-5)+9+(-6)+7 = ____
2. 绝对值小于5的所有整数的和为_ _ ____
3. 在括号里填写每步运算的根据:
(-8)+(-5)+8
=(-8)+8+(-5) ( )
=〔(-8)+8〕+(-5) ( )
=0+(-5) ( )
=-5 ( )
加法交换律
加法结合律
互为相反数的两数之和为0
0与任何数相加仍得这个数
5
0
能力提升
计算:
4 . -1+2+(-3)+4+ …+2015+(-2016)
拓展
5. 小虫从某点O出发,在一直线上来回爬行,假定向右爬行记为正数,向左爬行记为负数,爬行的过程依次为(单位:厘米):
+5, -3,+10, -8, -6, +12, -13.
试问:(1)小虫最后能否回到出发点O?
(2)若不在点O,小虫在哪里?
(3)小虫爬行的总路程是多少?
1、(+2)+( )=+1
试一试:
2、(-3)+( )= -10
3、( )+ ( -5 )= 1.5
4、( )+( + )= 1.5
5、(+0.1 )+( )= 0
6、 +( )= 2
1.使用加法运算律, 可使运算简便.
课堂小结:
1.你对你自己的表现如何?
2.你对同桌的的学习表现如何?
3.通过这节课的学习,你有什么收获?
体会:
2.培养了概括力和符号感.
5 - (-3) = _____?
一天中的最高气温与最低气温的差叫做日温差.
如果某天最高气温是5℃,最低气温是-3℃,
那么这天的日温差是_____.
8℃
小学里学过减法是加法的逆运算.因为8+(-3)=5,所以5-(-3)=8.
加法
减法
从上往下看,从5℃到-3℃,温度下降了5+3=8℃
于是得到 5-(-3)= 5+3
5 -(-3) = 8
5 + 3 = 8
减号变为加号
-3变成它的相反数3
总 结
有理数减法法则
减去一个数,等于加上这个数的相反数.
【试一试】
填空:
(1)(-3)-5 = (-3)+____
(2) 3-(-5) = 3+____
(-5)
5
(3) 3-5 = 3+____
(-5)
(4) (-3)-(-5) =(-3)+____
5
【例题精讲】
例1、计算
(2) 8.5-(-1.5)
(1) 0-(-22)
(4)
(3) (+4)-16
练习1:
(1) 3 – 5 ; (2) 3 – ( – 5);
(3)( – 3)– 5; (4)(– 3) –( –5);
(5)( – 6)– 6; (6) 6-(-6) ;
(7) (–6)–(–6) ; (8)– 7 – 0 .
例2、根据天气
预报图, 计算
右图中各城市
的日温差.
【例题精讲】
分别输入0,1,-1,按图所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行计算).并写出输出的结果.
输入
+4
-(-3)
-5
>2
输出
是
否
练习2:
(1)( )+(-8)=-12;
(2)(+8)+( )=-12;
(3)( )-(-7.1)=8;
(4)(-2)-( )=-7;
(5)在数轴上表示数7的点与表示-1的点之间
的距离是 ;
表示数-2的点与表示-6的点之间的距离
是 .
你能发现所得的距离与这两数的差有什么关系吗
【能力升级】
(6) 已知|a|=5,|b|=3,则a-b的值为____.
例4、计算
(1) (-20)-7-(-13)-(-16)
(2) (-3.4)+5.8-(+8.6)+12
【例题精讲】
练习3:
计算:
(1) 7-(-4)+(-5)
(2)(-21)-12+33+12-67
有理数的加法法则和减法法则
(1)5-8
计算:
(2)2+5-8
(3)14-(-12)+(-25)-17
有理数的加减混合运算可以统一成加法运算
(1)-3-5+4
(2)
例1、计算:
例如:-3+(-5)+4 可以写成 -3-5+4
在把有理数加减混合运算统一为加法的算式中,
负数前面的加号可以省略不写.
也就是 -3-5+4 表示 -3、-5与4 的和.
(1) -3-5+4
(2) -26+43-24+13-46
【例题精讲】
例2、计算:
练习:计算
(1)-21-12+33+12-67
(3)
(2)5.4-2.3+1.5-4.2
(1)(-5)-(-12)+(-7)-(+8)
(3)(-4)+9-(-7)-13
(2)
【例题精讲】
例3、计算
例4:若a=-3,b=2,c=-4,求下列各值:
(1)、a+b-c
(3)、a-b+c
(2)、
(4)、-a-b-c
【例题精讲】
【例题精讲】
例5、巡道员沿东西方向的铁路进行巡视维护.
他从住地出发,先向东行走了7km,休息之后
继续向东行走了3km;然后折返向西行走了11.5km.此时他在住地的什么方向?与住地的
距离是多少?
思考
(1)、当b>0时,a,a-b,a+b 哪个最大?哪个最小?
(2)、当b<0时,a,a-b,a+b 哪个最大?哪个最小?
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
