湘教版七年级上册数学1.6有理数的乘方课件(22张ppt)
文档属性
| 名称 | 湘教版七年级上册数学1.6有理数的乘方课件(22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览






文档简介
1.6 有理数的乘方
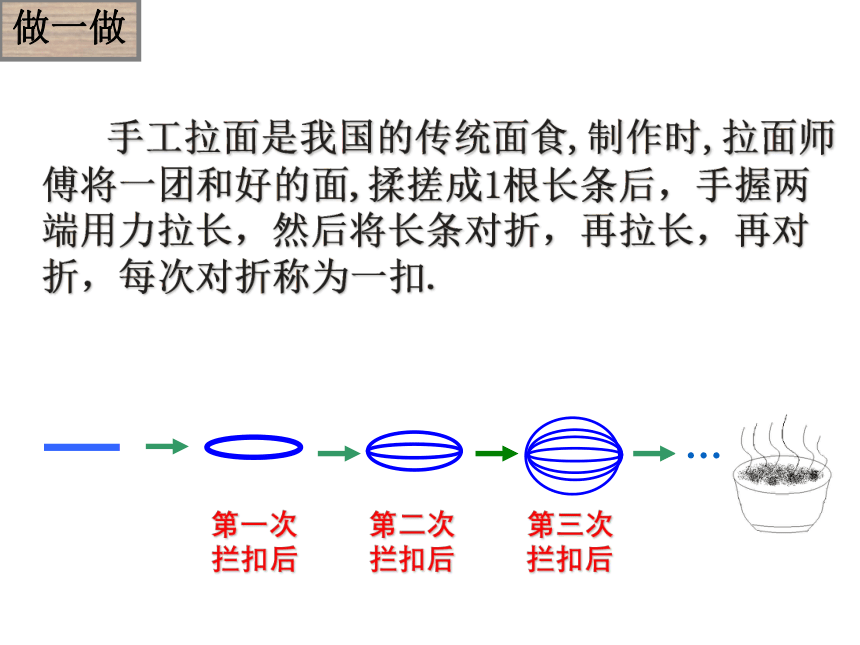
手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣.
第一次
拦扣后
第二次
拦扣后
第三次
拦扣后
…
做一做
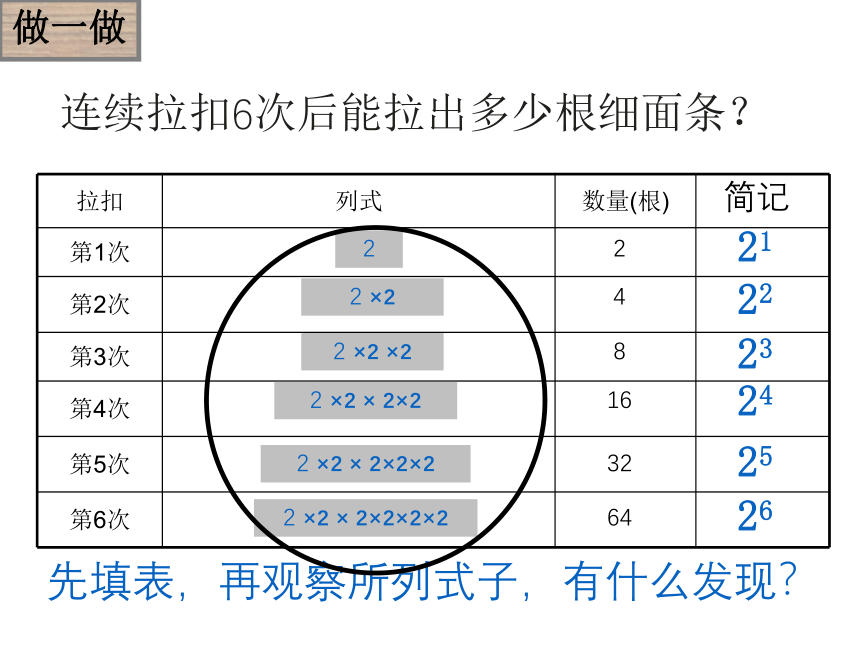
连续拉扣6次后能拉出多少根细面条?
拉扣
列式
数量(根)
第1次
第2次
第3次
第4次
第5次
第6次
简记
2
2 ×2
2 ×2 ×2
2 ×2 × 2×2
22
23
24
21
2
4
8
16
2 ×2 × 2×2×2
32
2 ×2 × 2×2×2×2
64
25
26
先填表,再观察所列式子,有什么发现?
做一做
问题一:(-2) × (-2) × (-2) × (-2) × (-2)
简记为
动动脑
(-2)5
问题二:a× a× a × a × a × a × a
简记为
问题三: a×a×a×……×a 简记为
n个a
a7
an
一般地,a是有理数,n是正整数,则把
a × a × a ×…×a 简记作an,即
n个
an =a × a × a ×…×a.
n个
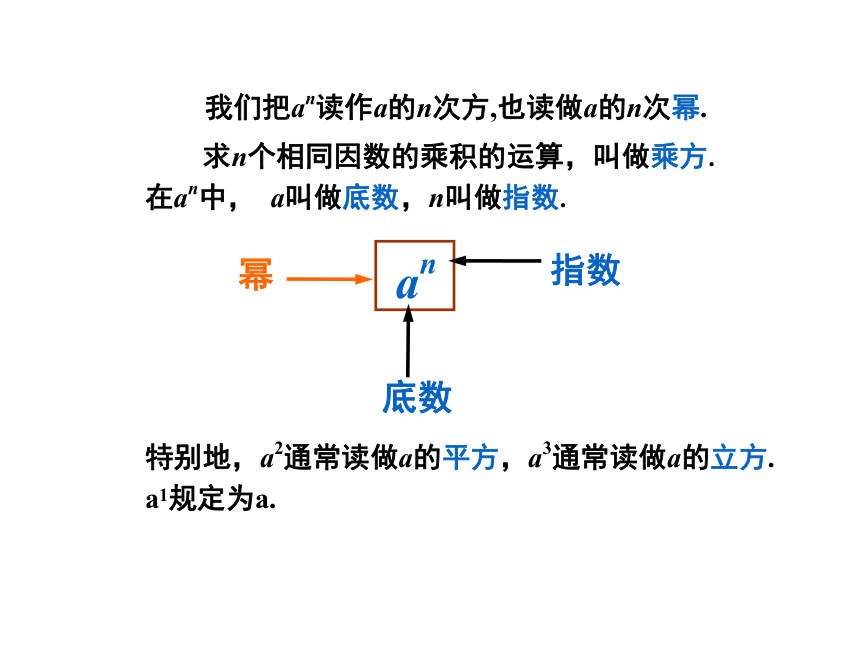
我们把an读作a的n次方,也读做a的n次幂.
求n个相同因数的乘积的运算,叫做乘方.
在an中, a叫做底数,n叫做指数.
我们把an读作a的n次方,也读做a的n次幂.
an
幂
底数
指数
特别地,a2通常读做a的平方,a3通常读做a的立方.
a1规定为a.
(-2)4与-24的含义相同吗?它们的结果相同吗?(-2)3与-23的含义与结果也分别相同吗?
(-2)4表示-2的4次方.
-24表示2的4次方的相反数.
……
议一议:
例1 计算:
(1) (-3)3 ; (2) 07 ;
(3) ; (4) .
举
例
解
(1) (-3)3
= (-3)×(-3)×(-3)
(-3)的3次方,是3个(-3)相乘
3个(-3)相乘,结果为负
= -27;
解
(2) 07
= 0× 0× 0× 0× 0× 0× 0
0的7次方,结果还为0
= 0;
解
(3)
=
计算结果
解
(4)
=
4个负数相乘,结果为正
=
的三次方,是3个 相乘
=
的四次方,是4个 相乘
正数的任何正整数次幂都是什么数?
正数的任何正整数次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
负数的偶次幂是什么数?
负数的奇次幂是什么数?
0的任何正整数次幂是多少?
说一说:
例2 计算:
(1) ;
(2) -23 ×(-2)2 .
举
例
= 4;
解
= -8×4
= -32.
(1)
解
(2) -23 ×(-2)2 .
1.填表:
底数
-1
2
10
指数
3
5
4
幂
(-4)3
0.34
(-1)3
25
-4
3
4
0.3
104
2.判断:(对的画“√”,错的画“×”)
(1) 32 = 3×2 = 6 ( )
(2) (-2)3 = (-3)2 ( )
(3) -32 = (-3)2 ( )
×
×
×
练一练
(1) (-3)4; (2) (-2)5;
(3) (0)5 ; (4) .
解: (1) (-3)4 =(-3)×(-3)×(-3)×(-3)=81;
(2) (-2)5 =(-2)×(-2)×(-2)×(-2)×(-2)=-32;
(4) = × × = .
(3) (0)5 =(0)×(0)×(0)×(0) ×(0)=0;
3.计算:
在日常生活中,我们会遇到一些较大的数,如地球的表面积约为 511 000 000 km2,能不能用一种较简单的方式来表示这样的大数?
5.11×108
1. 102,103,104,… ,10n分别等于多少?你发现了什么?
探究
102= 100, 103= 1000
104= 10000 ,…,
10n= 1 000…0 .
2个0
3个0
4个0
n个0
10的n次幂就是1后面有n个0.
我们可以利用10的乘方来表示一些大数,
把一个绝对值大于10的数记做a×10n的形式,其中a是整数数位只有一位的数(即1≤|a|<10),这种记数法叫做科学记数法.
例如,
511000000 = 5.11× 100000000 = 5.11×108,
读做5.11乘10的8次方.
例3 用科学记数法表示下列各数:
(1)108 000 000; (2)-32 000 000.
(1)108 000 000=1.08×108;
解:
(2)-32 000 000= -3.2×107.
举
例
例4 2010年11月14日,半年评选一次的全球超级计算机500强名单正式公布,我国“天河一号”超级计算机以每秒2570万亿次的实测运算速度,成为世界运算最快的超级计算机.请用科学记数法表示“天河一号”的实测运算速度为每秒多少次.
解: 2570万亿就是2570000000000000.
用科学记数法表示为2.57 × 1015,
即“天河一号”的实测运算速度为
每秒2.57 × 1015次.
举
例
某种细胞每过30分钟便由1个分裂成2个.经过24小时,这种细胞由1个能分裂成多少个?
练一练:
248 = 281474976710656(个)
解:
每30分钟分裂一次,24小时后能分裂48次.
答:经过24小时,这种细胞由1个约能分裂成2.8×1014个.
≈2.8×1014(个)
课堂小结:
an读作a的n次方,也读做a的n次幂. 特别地,a2通常读做a的平方,a3通常读做a的立方.
求n个相同因数的乘积的运算,叫做乘方.在an中, a叫做底数,n叫做指数.
把一个绝对值大于10的数记做a×10n的形式,其中a是整数数位只有一位的数(即1≤|a|<10),这种记数法叫做科学记数法.
手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣.
第一次
拦扣后
第二次
拦扣后
第三次
拦扣后
…
做一做
连续拉扣6次后能拉出多少根细面条?
拉扣
列式
数量(根)
第1次
第2次
第3次
第4次
第5次
第6次
简记
2
2 ×2
2 ×2 ×2
2 ×2 × 2×2
22
23
24
21
2
4
8
16
2 ×2 × 2×2×2
32
2 ×2 × 2×2×2×2
64
25
26
先填表,再观察所列式子,有什么发现?
做一做
问题一:(-2) × (-2) × (-2) × (-2) × (-2)
简记为
动动脑
(-2)5
问题二:a× a× a × a × a × a × a
简记为
问题三: a×a×a×……×a 简记为
n个a
a7
an
一般地,a是有理数,n是正整数,则把
a × a × a ×…×a 简记作an,即
n个
an =a × a × a ×…×a.
n个
我们把an读作a的n次方,也读做a的n次幂.
求n个相同因数的乘积的运算,叫做乘方.
在an中, a叫做底数,n叫做指数.
我们把an读作a的n次方,也读做a的n次幂.
an
幂
底数
指数
特别地,a2通常读做a的平方,a3通常读做a的立方.
a1规定为a.
(-2)4与-24的含义相同吗?它们的结果相同吗?(-2)3与-23的含义与结果也分别相同吗?
(-2)4表示-2的4次方.
-24表示2的4次方的相反数.
……
议一议:
例1 计算:
(1) (-3)3 ; (2) 07 ;
(3) ; (4) .
举
例
解
(1) (-3)3
= (-3)×(-3)×(-3)
(-3)的3次方,是3个(-3)相乘
3个(-3)相乘,结果为负
= -27;
解
(2) 07
= 0× 0× 0× 0× 0× 0× 0
0的7次方,结果还为0
= 0;
解
(3)
=
计算结果
解
(4)
=
4个负数相乘,结果为正
=
的三次方,是3个 相乘
=
的四次方,是4个 相乘
正数的任何正整数次幂都是什么数?
正数的任何正整数次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
负数的偶次幂是什么数?
负数的奇次幂是什么数?
0的任何正整数次幂是多少?
说一说:
例2 计算:
(1) ;
(2) -23 ×(-2)2 .
举
例
= 4;
解
= -8×4
= -32.
(1)
解
(2) -23 ×(-2)2 .
1.填表:
底数
-1
2
10
指数
3
5
4
幂
(-4)3
0.34
(-1)3
25
-4
3
4
0.3
104
2.判断:(对的画“√”,错的画“×”)
(1) 32 = 3×2 = 6 ( )
(2) (-2)3 = (-3)2 ( )
(3) -32 = (-3)2 ( )
×
×
×
练一练
(1) (-3)4; (2) (-2)5;
(3) (0)5 ; (4) .
解: (1) (-3)4 =(-3)×(-3)×(-3)×(-3)=81;
(2) (-2)5 =(-2)×(-2)×(-2)×(-2)×(-2)=-32;
(4) = × × = .
(3) (0)5 =(0)×(0)×(0)×(0) ×(0)=0;
3.计算:
在日常生活中,我们会遇到一些较大的数,如地球的表面积约为 511 000 000 km2,能不能用一种较简单的方式来表示这样的大数?
5.11×108
1. 102,103,104,… ,10n分别等于多少?你发现了什么?
探究
102= 100, 103= 1000
104= 10000 ,…,
10n= 1 000…0 .
2个0
3个0
4个0
n个0
10的n次幂就是1后面有n个0.
我们可以利用10的乘方来表示一些大数,
把一个绝对值大于10的数记做a×10n的形式,其中a是整数数位只有一位的数(即1≤|a|<10),这种记数法叫做科学记数法.
例如,
511000000 = 5.11× 100000000 = 5.11×108,
读做5.11乘10的8次方.
例3 用科学记数法表示下列各数:
(1)108 000 000; (2)-32 000 000.
(1)108 000 000=1.08×108;
解:
(2)-32 000 000= -3.2×107.
举
例
例4 2010年11月14日,半年评选一次的全球超级计算机500强名单正式公布,我国“天河一号”超级计算机以每秒2570万亿次的实测运算速度,成为世界运算最快的超级计算机.请用科学记数法表示“天河一号”的实测运算速度为每秒多少次.
解: 2570万亿就是2570000000000000.
用科学记数法表示为2.57 × 1015,
即“天河一号”的实测运算速度为
每秒2.57 × 1015次.
举
例
某种细胞每过30分钟便由1个分裂成2个.经过24小时,这种细胞由1个能分裂成多少个?
练一练:
248 = 281474976710656(个)
解:
每30分钟分裂一次,24小时后能分裂48次.
答:经过24小时,这种细胞由1个约能分裂成2.8×1014个.
≈2.8×1014(个)
课堂小结:
an读作a的n次方,也读做a的n次幂. 特别地,a2通常读做a的平方,a3通常读做a的立方.
求n个相同因数的乘积的运算,叫做乘方.在an中, a叫做底数,n叫做指数.
把一个绝对值大于10的数记做a×10n的形式,其中a是整数数位只有一位的数(即1≤|a|<10),这种记数法叫做科学记数法.
同课章节目录
