人教版 初中数学八年级上册12.2全等三角形性质与判定小结与复习课件 (共23张PPT)
文档属性
| 名称 | 人教版 初中数学八年级上册12.2全等三角形性质与判定小结与复习课件 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 296.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:34:14 | ||
图片预览






文档简介
(共24张PPT)
全等三角形性质与判定
小结复习
1.全等三角形的性质:
对应角相等、对应边相等。
2.全等三角形的判定:
知识点
①一般三角形全等的判定:
SAS
②直角三角形全等的判定:
SSS、
SAS、ASA、AAS
温故而知新
SSS
ASA
AAS
HL
1
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
2
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
3
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
知识回顾
5
如果两个直角三角形的斜边和及一条直角边分别对应相等,那么这两个直角三角形全等(可以简写成“斜边直角边”或“HL”)。
4
有两角和其中一个角的对边对应相等的两个三角形全等(可以
简写成“角角边”或“AAS”)。
1、判断下列说法正确还是错误
(1)有两边一角对应相等的两个三角形全等.
(2)判定两个三角形全等的条件中至少有一边相等.
(3)两个锐角对应相等的两个直角三角形全等.
(4)有两组边相等且周长相等的两个三角形全等.
基础过关
2、下列判断正确的是(
)
A、等边三角形都全等
B、面积相等的两个三角形全等
C、腰长对应相等的两个等腰三角形全等
D、直角三角形和钝角三角形不可能全等
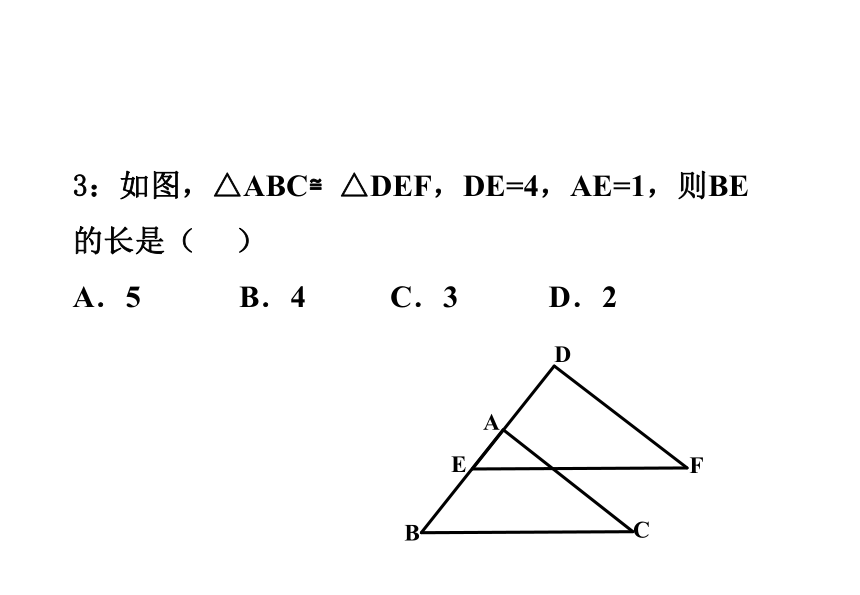
3:如图,△ABC≌△DEF,DE=4,AE=1,则BE的长是(
)
A.5
B.4
C.3
D.2
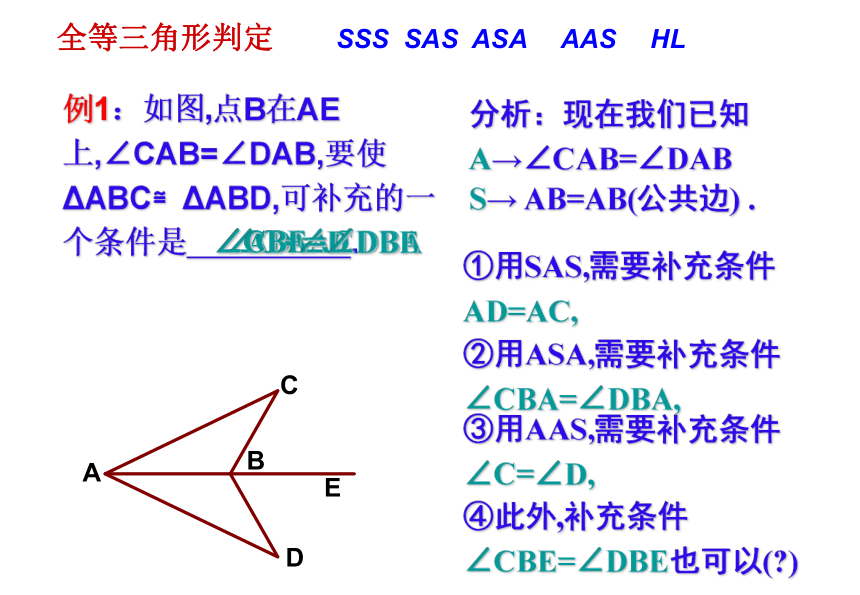
例1:如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是
.
分析:现在我们已知
A→∠CAB=∠DAB
①用SAS,需要补充条件AD=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以(?)
S→
AB=AB(公共边)
.
AD=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
全等三角形判定 SSS
SAS
ASA
AAS
HL
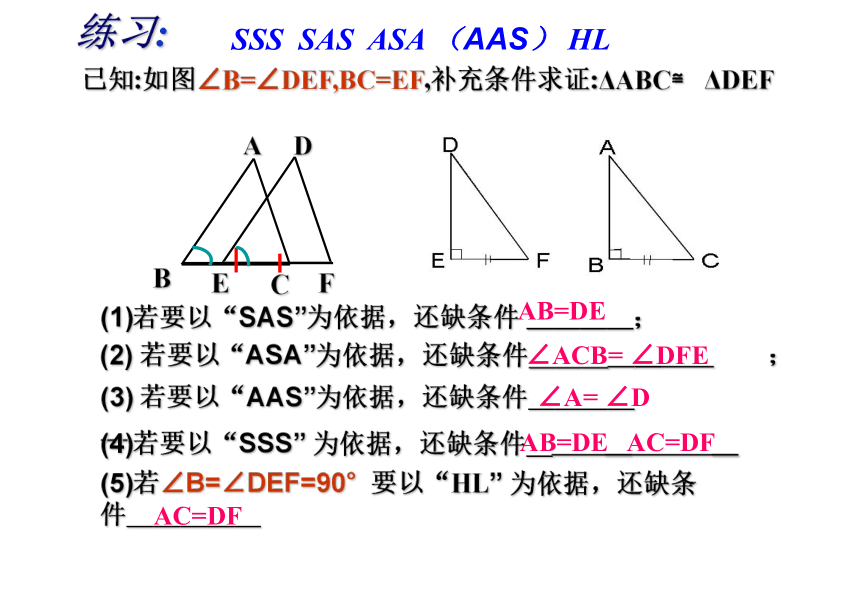
练习:
已知:如图∠B=∠DEF,BC=EF,补充条件求证:ΔABC≌
ΔDEF
D
E
F
A
B
C
(1)若要以“SAS”为依据,还缺条件
____;
AB=DE
(2)
若要以“ASA”为依据,还缺条件___ _ ;
∠ACB=
∠DFE
(3)
若要以“AAS”为依据,还缺条件_____
∠A=
∠D
(4)若要以“SSS”
为依据,还缺条件_ _ _
AB=DE
AC=DF
(5)若∠B=∠DEF=90°要以“HL”
为依据,还缺条件_____
AC=DF
SSS
SAS
ASA
(AAS)
HL
例2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是拿(
)去配.
发现:题目中的隐含条件通常有:
公共边、公共角、对顶角
探索归纳
如图已知∠CAB=∠DAB,AC
=
AD,
△ABC
是否与△ABD全等?为什么?
解:
△ABC
≌△ABD
理由:在△ABC
与△ABD中
AC
=
AD
∠CAB
=∠DAB
AB
=
AB
∴
ABC
≌△ABD
C
B
D
A
(一)
练习1.
已知:如图,
△ABC和△CDB中,AB=DC,AC=DB
求证:
∠ABD=
∠
DCA
O
证明两个角相等的方法有哪些?
证明:
∵
∠1=∠2
∴
∠1+
∠EAD=∠2
+∠EAD
即∠BAD
=
∠CAE
在△BAD
与△CAE中
AB
=
AC
∠BAD
=
∠CAE
AE
=
AD
∴
△
ABD≌△
ACE
∴
CE=BD
如图已知∠1=∠2,AB
=
AC,AE
=
AD,求证:CE
=BD
B
D
E
C
B
A
1
2
(二)
A
B
C
E
F
练习1
已知:如图,
△AEF
与△ABC中,
∠E
=∠B,
EF=BC.请你添加一个条件,使△AEF
≌
△ABC.
对于添加条件使两三角形全等的问题,当已有两个条件(包括隐含条件)时,如何思考?
2.
如图,点B、E、C、F在一条直线上,AB=DE,AB∥DE,∠A=∠D.
求证:BE=CF.
证明两条线段相等的方法有哪些?
3.如图所示,CD,C'D'分别是Rt?ABC,Rt?A'B'C'斜边上的高且CB=C'B',CD=C'D'.
求证?ABC≌?A'B'C'
A
A'
C
D
C
'
B'
D'
B'
1.如图1:△ABF≌
△CDE,∠B=30°,
∠BAE=
∠DCF=20
°.求∠EFC的度数.
练习题:
2
、如图2,已知:AD平分∠BAC,AB=AC,连接BD,CD,并延长相交AC、AB于F、E点.则图形中有(?
)对全等三角形.
A、2 B、3 C4 D、5
C
图1
图2
3、如图3,已知:△ABC中,DF=FE,BD=CE,AF⊥BC于F,则此图中全等三角形共有(?
)
A、5对 B、4对 C、3对 D2对
?????????????????????????????????????????????????????????????????????????????????????????????????????????
B
4.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=145°,则∠EDF=
.
55°
7.
如图,∠ACB=∠ADB=90°,AC=AD,点E在AB上,求证:CE=DE.
证明:Rt△ACB和Rt△ADB中,
∵∠ACB=∠ADB=90°
∴Rt△ACB≌Rt△ADB(HL),
∴∠1=∠2.在△ACE和△ADE中,∴△ACE≌△ADE,∴CE=DE.
8、如图4,已知:在△ABC中,AD是BC边上的高,AD=BD,DE=DC,延长BE交AC于F,
求证:BF是△ABC中边上的高.
小结:
1、全等三角形的定义,性质,判定方法。
2、证明题的方法
①要证什么
②已有什么
③还缺什么
④创造条件
3、添加辅助线
1.如图,∠BAC=90°,AB=AC,过点A作直线DE,且作CE⊥ED,BD⊥ED,若CE=2,BD=6,求DE长
小测:
必做题
选做题
2.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,添加下列条件能使△AEH≌△CEB的有(
)
①AE=EC;②AH=BC;③EH=BE;
④∠EAH=∠B.
A.①②④
B.①②③
C.②③④
D.①③④
全等三角形性质与判定
小结复习
1.全等三角形的性质:
对应角相等、对应边相等。
2.全等三角形的判定:
知识点
①一般三角形全等的判定:
SAS
②直角三角形全等的判定:
SSS、
SAS、ASA、AAS
温故而知新
SSS
ASA
AAS
HL
1
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
2
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
3
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
知识回顾
5
如果两个直角三角形的斜边和及一条直角边分别对应相等,那么这两个直角三角形全等(可以简写成“斜边直角边”或“HL”)。
4
有两角和其中一个角的对边对应相等的两个三角形全等(可以
简写成“角角边”或“AAS”)。
1、判断下列说法正确还是错误
(1)有两边一角对应相等的两个三角形全等.
(2)判定两个三角形全等的条件中至少有一边相等.
(3)两个锐角对应相等的两个直角三角形全等.
(4)有两组边相等且周长相等的两个三角形全等.
基础过关
2、下列判断正确的是(
)
A、等边三角形都全等
B、面积相等的两个三角形全等
C、腰长对应相等的两个等腰三角形全等
D、直角三角形和钝角三角形不可能全等
3:如图,△ABC≌△DEF,DE=4,AE=1,则BE的长是(
)
A.5
B.4
C.3
D.2
例1:如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是
.
分析:现在我们已知
A→∠CAB=∠DAB
①用SAS,需要补充条件AD=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以(?)
S→
AB=AB(公共边)
.
AD=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
全等三角形判定 SSS
SAS
ASA
AAS
HL
练习:
已知:如图∠B=∠DEF,BC=EF,补充条件求证:ΔABC≌
ΔDEF
D
E
F
A
B
C
(1)若要以“SAS”为依据,还缺条件
____;
AB=DE
(2)
若要以“ASA”为依据,还缺条件___ _ ;
∠ACB=
∠DFE
(3)
若要以“AAS”为依据,还缺条件_____
∠A=
∠D
(4)若要以“SSS”
为依据,还缺条件_ _ _
AB=DE
AC=DF
(5)若∠B=∠DEF=90°要以“HL”
为依据,还缺条件_____
AC=DF
SSS
SAS
ASA
(AAS)
HL
例2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是拿(
)去配.
发现:题目中的隐含条件通常有:
公共边、公共角、对顶角
探索归纳
如图已知∠CAB=∠DAB,AC
=
AD,
△ABC
是否与△ABD全等?为什么?
解:
△ABC
≌△ABD
理由:在△ABC
与△ABD中
AC
=
AD
∠CAB
=∠DAB
AB
=
AB
∴
ABC
≌△ABD
C
B
D
A
(一)
练习1.
已知:如图,
△ABC和△CDB中,AB=DC,AC=DB
求证:
∠ABD=
∠
DCA
O
证明两个角相等的方法有哪些?
证明:
∵
∠1=∠2
∴
∠1+
∠EAD=∠2
+∠EAD
即∠BAD
=
∠CAE
在△BAD
与△CAE中
AB
=
AC
∠BAD
=
∠CAE
AE
=
AD
∴
△
ABD≌△
ACE
∴
CE=BD
如图已知∠1=∠2,AB
=
AC,AE
=
AD,求证:CE
=BD
B
D
E
C
B
A
1
2
(二)
A
B
C
E
F
练习1
已知:如图,
△AEF
与△ABC中,
∠E
=∠B,
EF=BC.请你添加一个条件,使△AEF
≌
△ABC.
对于添加条件使两三角形全等的问题,当已有两个条件(包括隐含条件)时,如何思考?
2.
如图,点B、E、C、F在一条直线上,AB=DE,AB∥DE,∠A=∠D.
求证:BE=CF.
证明两条线段相等的方法有哪些?
3.如图所示,CD,C'D'分别是Rt?ABC,Rt?A'B'C'斜边上的高且CB=C'B',CD=C'D'.
求证?ABC≌?A'B'C'
A
A'
C
D
C
'
B'
D'
B'
1.如图1:△ABF≌
△CDE,∠B=30°,
∠BAE=
∠DCF=20
°.求∠EFC的度数.
练习题:
2
、如图2,已知:AD平分∠BAC,AB=AC,连接BD,CD,并延长相交AC、AB于F、E点.则图形中有(?
)对全等三角形.
A、2 B、3 C4 D、5
C
图1
图2
3、如图3,已知:△ABC中,DF=FE,BD=CE,AF⊥BC于F,则此图中全等三角形共有(?
)
A、5对 B、4对 C、3对 D2对
?????????????????????????????????????????????????????????????????????????????????????????????????????????
B
4.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=145°,则∠EDF=
.
55°
7.
如图,∠ACB=∠ADB=90°,AC=AD,点E在AB上,求证:CE=DE.
证明:Rt△ACB和Rt△ADB中,
∵∠ACB=∠ADB=90°
∴Rt△ACB≌Rt△ADB(HL),
∴∠1=∠2.在△ACE和△ADE中,∴△ACE≌△ADE,∴CE=DE.
8、如图4,已知:在△ABC中,AD是BC边上的高,AD=BD,DE=DC,延长BE交AC于F,
求证:BF是△ABC中边上的高.
小结:
1、全等三角形的定义,性质,判定方法。
2、证明题的方法
①要证什么
②已有什么
③还缺什么
④创造条件
3、添加辅助线
1.如图,∠BAC=90°,AB=AC,过点A作直线DE,且作CE⊥ED,BD⊥ED,若CE=2,BD=6,求DE长
小测:
必做题
选做题
2.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,添加下列条件能使△AEH≌△CEB的有(
)
①AE=EC;②AH=BC;③EH=BE;
④∠EAH=∠B.
A.①②④
B.①②③
C.②③④
D.①③④
