2020-2021学年苏科版九年级数学上册2.5直线与圆的位置关系专题培优训练卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学上册2.5直线与圆的位置关系专题培优训练卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 13:00:55 | ||
图片预览

文档简介
2020-2021学年苏科版九年级数学上册
第2章圆
2.5直线与圆的位置关系专题培优训练卷
一、选择题
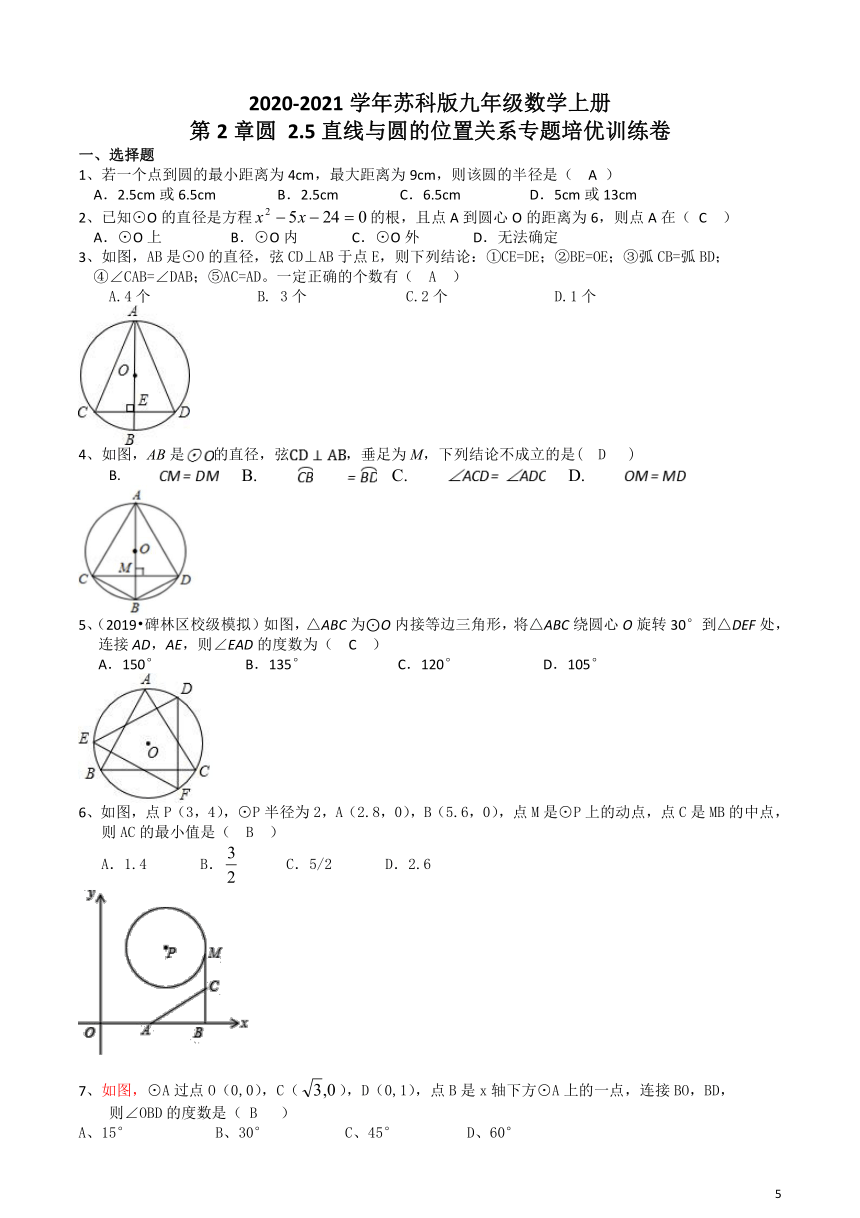
1、若一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(
)
A.2.5cm或6.5cm
B.2.5cm
C.6.5cm
D.5cm或13cm
2、已知⊙O的直径是方程的根,且点A到圆心O的距离为6,则点A在(
)
A.⊙O上
B.⊙O内
C.⊙O外
D.无法确定
3、如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论:①CE=DE;②BE=OE;③弧CB=弧BD;
④∠CAB=∠DAB;⑤AC=AD。一定正确的个数有(
)
A.4个
B.
3个
C.2个
D.1个
(3)
(4)
(5)
4、如图,AB是的直径,弦,垂足为M,下列结论不成立的是(
)
A.
B.
?
C.
D.
5、(2019?碑林区校级模拟)如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD,AE,则∠EAD的度数为( )
A.150°
B.135°
C.120°
D.105°
6、如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是(
)
A.1.4
B.
C.5/2
D.2.6
(6)
(7)
(8)
7、如图,⊙A过点O(0,0),C(),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,
则∠OBD的度数是(
)
A、15°
B、30°
C、45°
D、60°
8、如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,
则线段CP长的最小值为(
)
A、
B、2
C、
D、
9、直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6
B.r=6
C.r>6
D.r≥6
10、如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,
则弦长AB的取值范围是____
A.8≤AB≤10
B.AB≥8
C.8<AB≤10
D.8<AB<10
二、填空题
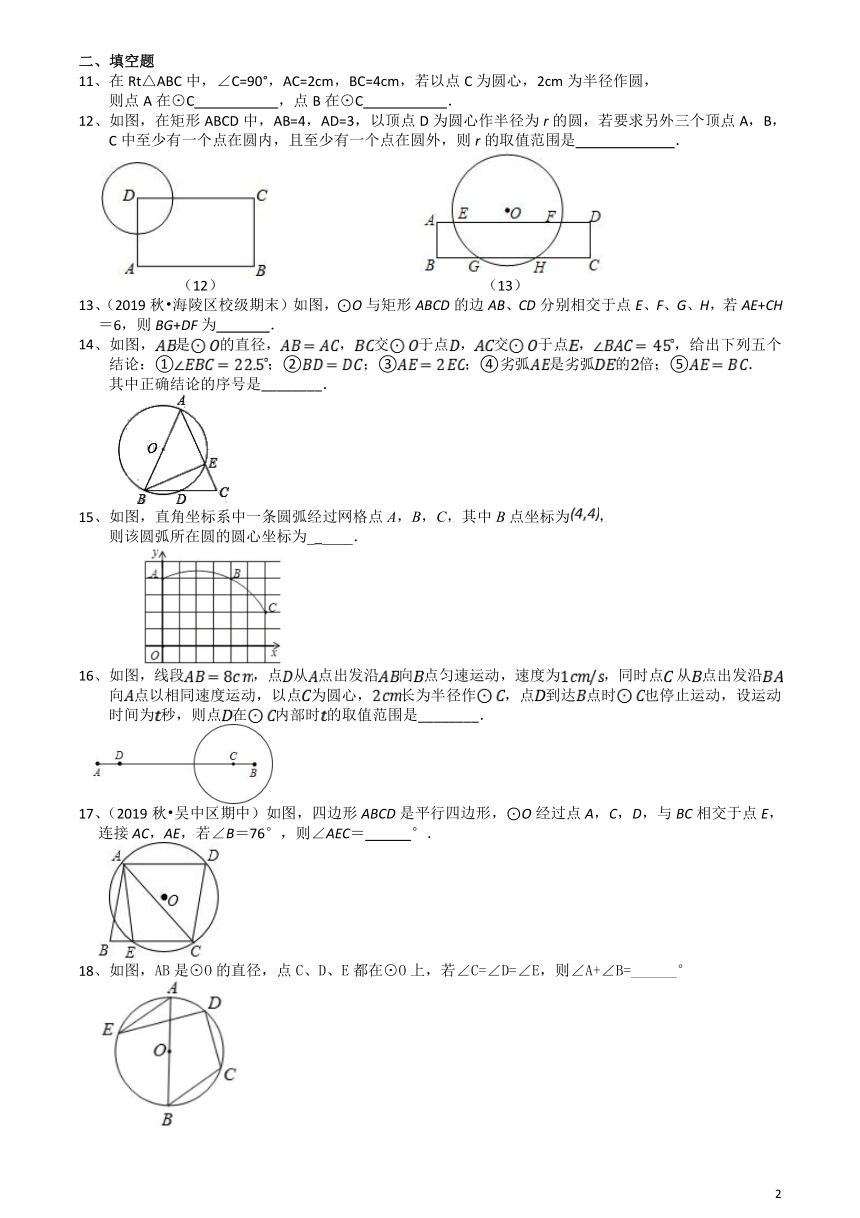
11、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
,点B在⊙C
.
12、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
.
(12)
(13)
13、(2019秋?海陵区校级期末)如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH=6,则BG+DF为
.
14、如图,是的直径,,交于点,交于点,,给出下列五个结论:①;②;③;④劣弧是劣弧的倍;⑤.
其中正确结论的序号是________.
15、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为,
则该圆弧所在圆的圆心坐标为______.
16、如图,线段,点从点出发沿向点匀速运动,速度为,同时点?从点出发沿向点以相同速度运动,以点为圆心,长为半径作,点到达点时也停止运动,设运动时间为秒,则点在内部时的取值范围是________.
17、(2019秋?吴中区期中)如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE,若∠B=76°,则∠AEC=
°.
18、如图,AB是⊙O的直径,点C、D、E都在⊙O上,若∠C=∠D=∠E,则∠A+∠B=______°
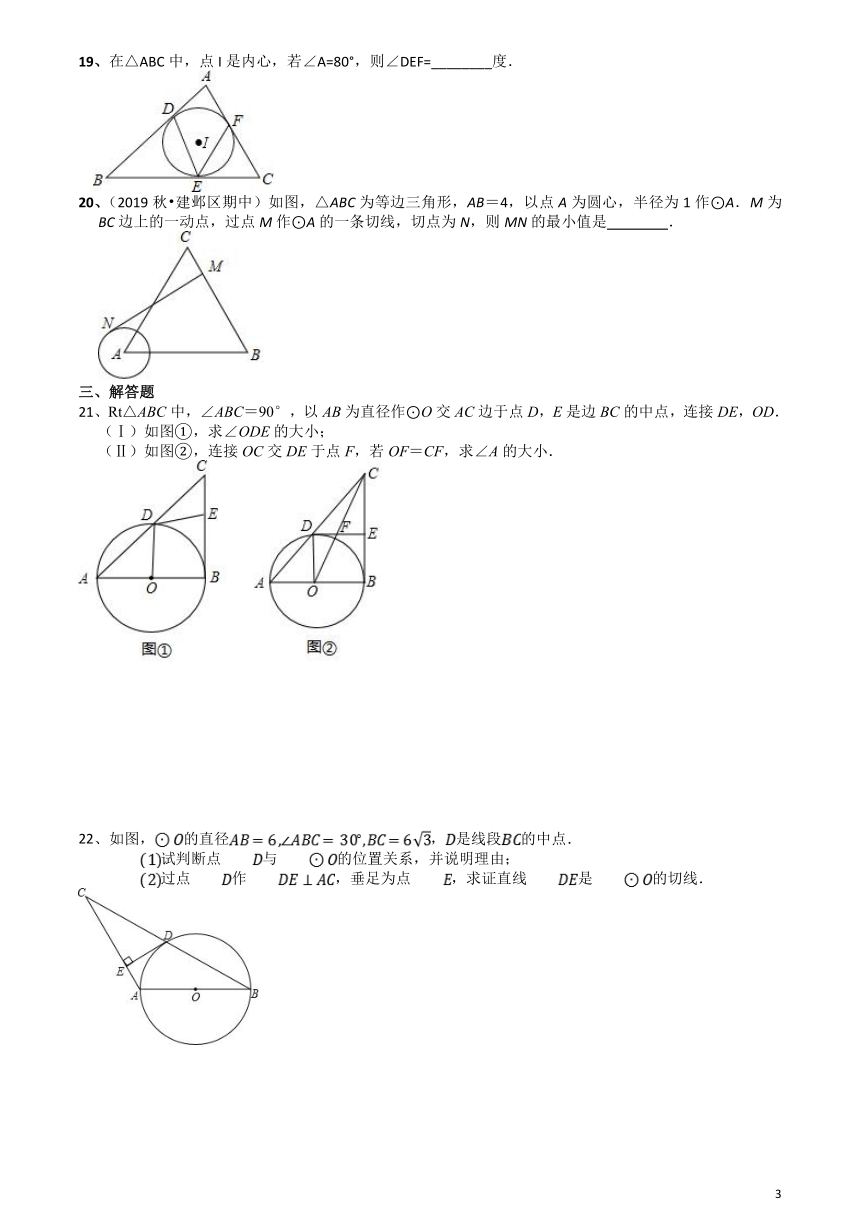
19、在△ABC中,点I是内心,若∠A=80°,则∠DEF=________度.
20、(2019秋?建邺区期中)如图,△ABC为等边三角形,AB=4,以点A为圆心,半径为1作⊙A.M为BC边上的一动点,过点M作⊙A的一条切线,切点为N,则MN的最小值是
.
三、解答题
21、Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.
22、如图,的直径,是线段的中点.
试判断点与的位置关系,并说明理由;?
过点作,垂足为点,求证直线是的切线.
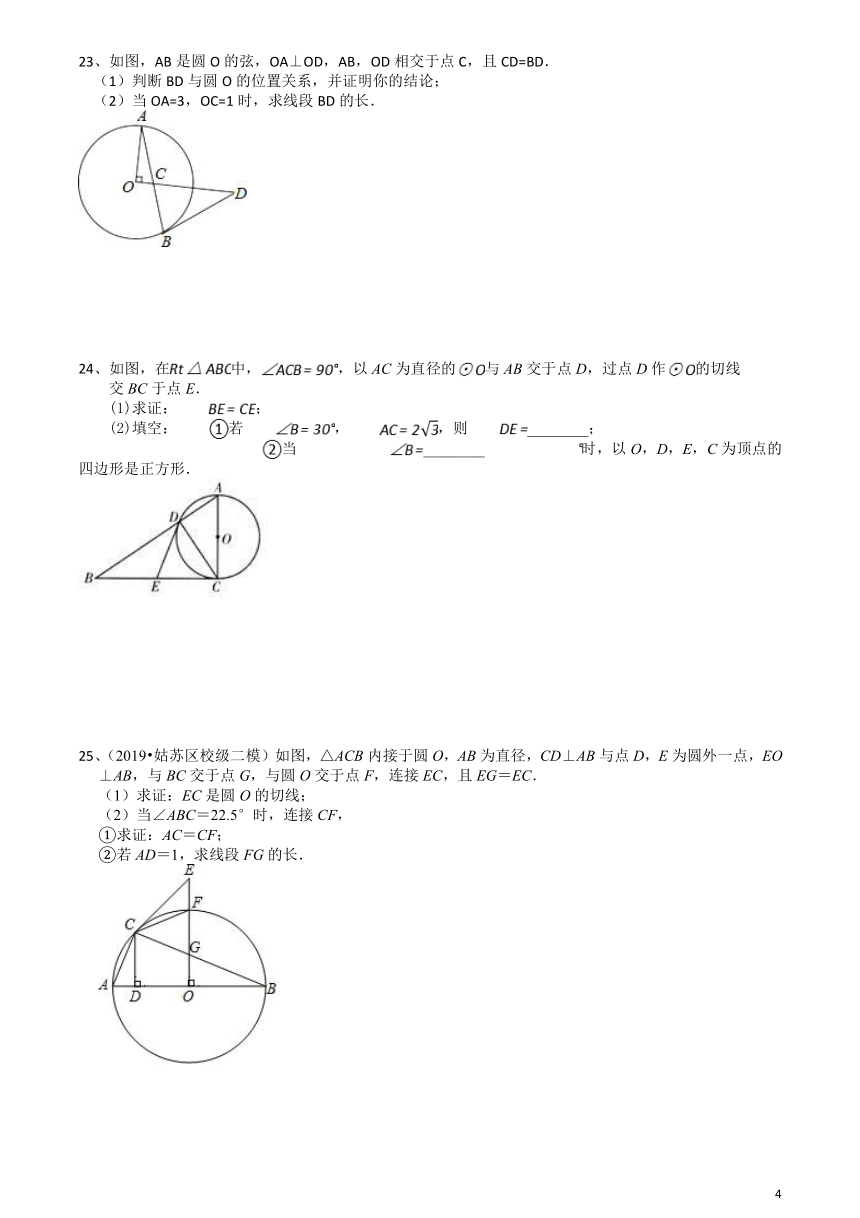
23、如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
?
24、如图,在中,,以AC为直径的与AB交于点D,过点D作的切线
交BC于点E.
(1)求证:;
(2)填空:若,,则________;
当________时,以O,D,E,C为顶点的四边形是正方形.
25、(2019?姑苏区校级二模)如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.
(1)求证:EC是圆O的切线;
(2)当∠ABC=22.5°时,连接CF,
①求证:AC=CF;
②若AD=1,求线段FG的长.
2020-2021学年苏科版九年级数学上册
第2章圆
2.5直线与圆的位置关系专题培优训练卷
一、选择题
1、若一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(
A
)
A.2.5cm或6.5cm
B.2.5cm
C.6.5cm
D.5cm或13cm
2、已知⊙O的直径是方程的根,且点A到圆心O的距离为6,则点A在(
C
)
A.⊙O上
B.⊙O内
C.⊙O外
D.无法确定
3、如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论:①CE=DE;②BE=OE;③弧CB=弧BD;
④∠CAB=∠DAB;⑤AC=AD。一定正确的个数有(
A
)
A.4个
B.
3个
C.2个
D.1个
4、如图,AB是的直径,弦,垂足为M,下列结论不成立的是(
D
)
B.
B.
?
C.
D.
5、(2019?碑林区校级模拟)如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD,AE,则∠EAD的度数为( C )
A.150°
B.135°
C.120°
D.105°
6、如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是(
B
)
A.1.4
B.
C.5/2
D.2.6
7、如图,⊙A过点O(0,0),C(),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,
则∠OBD的度数是(
B
)
A、15°
B、30°
C、45°
D、60°
8、如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,
则线段CP长的最小值为(
B
)
A、
B、2
C、
D、
9、直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是(C )
A.r<6
B.r=6
C.r>6
D.r≥6
10、如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,
则弦长AB的取值范围是_C___
A.8≤AB≤10
B.AB≥8
C.8<AB≤10
D.8<AB<10
二、填空题
11、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
上
,点B在⊙C
外
.
12、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
11.3.
13、(2019秋?海陵区校级期末)如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH=6,则BG+DF为
.
【分析】作OM⊥GH于M,OM交EF于N,如图,先证明OM⊥EF,利用垂径定理得到EN=FN,GM=HM,利用四边形ABMN和四边形MNDC为矩形得到AN=BM,DN=CM,然后根据等线段代换得到BG+DF=AE+CH.
【解答】解:作OM⊥GH于M,OM交EF于N,如图,
∵EF∥GH,∴OM⊥EF,∴EN=FN,GM=HM,
易得四边形ABMN和四边形MNDC为矩形,∴AN=BM,DN=CM,
∴BG+DF=BM﹣GM+DN﹣NF=AN﹣HM+CM﹣EN=AN﹣EN+CM﹣HM=AE+CH=6.
故答案为6.
14、如图,是的直径,,交于点,交于点,,给出下列五个结论:①;②;③;④劣弧是劣弧的倍;⑤.
其中正确结论的序号是________.
【答案】①②④
15、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为,
则该圆弧所在圆的圆心坐标为______.
16、如图,线段,点从点出发沿向点匀速运动,速度为,同时点?从点出发沿向点以相同速度运动,以点为圆心,长为半径作,点到达点时也停止运动,设运动时间为秒,则点在内部时的取值范围是________.
17、(2019秋?吴中区期中)如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE,若∠B=76°,则∠AEC= 104 °.
【分析】根据平行四边形的性质求出∠D,根据圆内接四边形的性质得出∠D+∠AEC=180°,代入求出即可.
【解析】∵四边形ABCD是平行四边形,∠B=76°,
∴∠D=∠B=76°,
∵四边形AECD是⊙O的内接四边形,
∴∠D+∠AEC=180°,
∴∠AEC=180°﹣76°=104°,
故答案为:104.
18、如图,AB是⊙O的直径,点C、D、E都在⊙O上,若∠C=∠D=∠E,则∠A+∠B=__135____°
19、在△ABC中,点I是内心,若∠A=80°,则∠DEF=________度.
解:连接IF,ID,
∵点I是内心,∴∠ADI=∠AFI=90°,
∵∠A=80°,∴∠DIF=100°,∴∠DEF=50°,故答案为:50.
20、(2019秋?建邺区期中)如图,△ABC为等边三角形,AB=4,以点A为圆心,半径为1作⊙A.M为BC边上的一动点,过点M作⊙A的一条切线,切点为N,则MN的最小值是 .
【分析】作AD⊥BC于D,过D作⊙A的一条切线,切点为E,连接AE,由等边三角形的性质和勾股定理得出AD2,由切线的性质得出AE⊥DE,由勾股定理求出DE,当点M与D重合时,N与E重合,此时MN最小.
【解析】作AD⊥BC于D,过D作⊙A的一条切线,切点为E,连接AE,如图所示:
∵△ABC是等边三角形,AD⊥BC,
∴BC=AB=4,BD=CDBC=2,
∴AD2,
∵DE是⊙A的一条切线,
∴AE⊥DE,AE=1,
∴DE,
当点M与D重合时,N与E重合,
此时MN最小,
故答案为:.
三、解答题
21、Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.
证明:(Ⅰ)连接OE,BD,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=90°,
∵E点是BC的中点,∴DE=BC=BE,
∵OD=OB,OE=OE,∴△ODE≌△OBE,∴∠ODE=∠OBE,
∵∠ABC=90°,∴∠ODE=90°;
(Ⅱ)∵CF=OF,CE=EB,∴FE是△COB的中位线,∴FE∥OB,∴∠AOD=∠ODE,
由(Ⅰ)得∠ODE=90°,∴∠AOD=90°,
∵OA=OD,∴∠A=∠ADO=.
22、如图,的直径,是线段的中点.
试判断点与的位置关系,并说明理由;?
过点作,垂足为点,求证直线是的切线.
解:点与的位置关系是在上,
理由是:
设交于,连接,
∵为的直径,∴,
∵,,∴,由勾股定理得:,
∵,为的中点,∴,即、互相重合,∴在上;
(2)
证明:连接,
∵为的中点,,∴,
∵,∴,∵为半径,∴直线是的切线.
23、如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
【答案】
(1)证明:连接OB,
∵OA=OB,DC=DB,∴∠A=∠ABO,∠DCB=∠DBC,
∵AO⊥OD,∴∠AOC=90°,即∠A+∠ACO=90°,
∵∠ACO=∠DCB=∠DBC,∴∠ABO+∠DBC=90°,即OB⊥BD,则BD为圆O的切线;
(2)解:设BD=x,则OD=x+1,而OB=OA=3,
在RT△OBD中,OB2+BD2=OD2
,
即32+x2=(x+1)2
,
解得x=4,∴线段BD的长是4.
?
24、如图,在中,,以AC为直径的与AB交于点D,过点D作的切线
交BC于点E.
(1)求证:;
(2)填空:若,,则________;
当________时,以O,D,E,C为顶点的四边形是正方形.
证明:连接DO.
,AC为直径,为的切线;
又也为的切线,,
又,,
又,,,;
解:,,,,
,
为直径,,
由得:,,故答案为3;
当时,四边形ODEC是正方形,理由如下:
,,
,,,,
,四边形DECO是矩形,
,矩形DECO是正方形.
25、(2019?姑苏区校级二模)如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.
(1)求证:EC是圆O的切线;
(2)当∠ABC=22.5°时,连接CF,
①求证:AC=CF;
②若AD=1,求线段FG的长.
【分析】(1)连接OC,证得OC⊥CE,即可证得结论;
(2)①通过证得∠AOC=45°=∠COF=45°,得出,即可证得AC=CF;
②作CM⊥OE于M,首先证得CF=CG,得出CM垂直平分FG,然后通过三角形平分线的性质证得CM=CD,即可证得Rt△ACD≌Rt△FCM,从而证得FM=AD=1,即可证得FG=2FM=2.
【答案】(1)证明:连接OC,
∵OC=OB,∴∠OCB=∠B,
∵EO⊥AB,∴∠OGB+∠B=90°,
∵EG=EC,∴∠ECG=∠EGC,
∵∠EGC=∠OGB,∴∠OCB+∠ECG=∠B+∠OGB=90°,∴OC⊥CE,
∴EC是圆O的切线;
(2)①证明:∵∠ABC=22.5°,∠OCB=∠B,∴∠AOC=45°,
∵EO⊥AB,∴∠COF=45°,∴,∴AC=CF;
②解:作CM⊥OE于M,
∵AB为直径,∴∠ACB=90°
∵∠ABC=22.5°,∠GOB=90°,∴∠A=∠OGB=∠67.5°,∴∠FGC=67.5°,
∵∠COF=45°,OC=OF,∴∠OFC=∠OCF=67.5°,∴∠GFC=∠FGC,
∴CF=CG,∴FM=GM,
∵∠AOC=∠COF,CD⊥OA,CM⊥OF,∴CD=DM,
在Rt△ACD和Rt△FCM中
∴Rt△ACD≌Rt△FCM(HL),∴FM=AD=1,∴FG=2FM=2.
第2章圆
2.5直线与圆的位置关系专题培优训练卷
一、选择题
1、若一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(
)
A.2.5cm或6.5cm
B.2.5cm
C.6.5cm
D.5cm或13cm
2、已知⊙O的直径是方程的根,且点A到圆心O的距离为6,则点A在(
)
A.⊙O上
B.⊙O内
C.⊙O外
D.无法确定
3、如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论:①CE=DE;②BE=OE;③弧CB=弧BD;
④∠CAB=∠DAB;⑤AC=AD。一定正确的个数有(
)
A.4个
B.
3个
C.2个
D.1个
(3)
(4)
(5)
4、如图,AB是的直径,弦,垂足为M,下列结论不成立的是(
)
A.
B.
?
C.
D.
5、(2019?碑林区校级模拟)如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD,AE,则∠EAD的度数为( )
A.150°
B.135°
C.120°
D.105°
6、如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是(
)
A.1.4
B.
C.5/2
D.2.6
(6)
(7)
(8)
7、如图,⊙A过点O(0,0),C(),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,
则∠OBD的度数是(
)
A、15°
B、30°
C、45°
D、60°
8、如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,
则线段CP长的最小值为(
)
A、
B、2
C、
D、
9、直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6
B.r=6
C.r>6
D.r≥6
10、如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,
则弦长AB的取值范围是____
A.8≤AB≤10
B.AB≥8
C.8<AB≤10
D.8<AB<10
二、填空题
11、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
,点B在⊙C
.
12、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
.
(12)
(13)
13、(2019秋?海陵区校级期末)如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH=6,则BG+DF为
.
14、如图,是的直径,,交于点,交于点,,给出下列五个结论:①;②;③;④劣弧是劣弧的倍;⑤.
其中正确结论的序号是________.
15、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为,
则该圆弧所在圆的圆心坐标为______.
16、如图,线段,点从点出发沿向点匀速运动,速度为,同时点?从点出发沿向点以相同速度运动,以点为圆心,长为半径作,点到达点时也停止运动,设运动时间为秒,则点在内部时的取值范围是________.
17、(2019秋?吴中区期中)如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE,若∠B=76°,则∠AEC=
°.
18、如图,AB是⊙O的直径,点C、D、E都在⊙O上,若∠C=∠D=∠E,则∠A+∠B=______°
19、在△ABC中,点I是内心,若∠A=80°,则∠DEF=________度.
20、(2019秋?建邺区期中)如图,△ABC为等边三角形,AB=4,以点A为圆心,半径为1作⊙A.M为BC边上的一动点,过点M作⊙A的一条切线,切点为N,则MN的最小值是
.
三、解答题
21、Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.
22、如图,的直径,是线段的中点.
试判断点与的位置关系,并说明理由;?
过点作,垂足为点,求证直线是的切线.
23、如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
?
24、如图,在中,,以AC为直径的与AB交于点D,过点D作的切线
交BC于点E.
(1)求证:;
(2)填空:若,,则________;
当________时,以O,D,E,C为顶点的四边形是正方形.
25、(2019?姑苏区校级二模)如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.
(1)求证:EC是圆O的切线;
(2)当∠ABC=22.5°时,连接CF,
①求证:AC=CF;
②若AD=1,求线段FG的长.
2020-2021学年苏科版九年级数学上册
第2章圆
2.5直线与圆的位置关系专题培优训练卷
一、选择题
1、若一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(
A
)
A.2.5cm或6.5cm
B.2.5cm
C.6.5cm
D.5cm或13cm
2、已知⊙O的直径是方程的根,且点A到圆心O的距离为6,则点A在(
C
)
A.⊙O上
B.⊙O内
C.⊙O外
D.无法确定
3、如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论:①CE=DE;②BE=OE;③弧CB=弧BD;
④∠CAB=∠DAB;⑤AC=AD。一定正确的个数有(
A
)
A.4个
B.
3个
C.2个
D.1个
4、如图,AB是的直径,弦,垂足为M,下列结论不成立的是(
D
)
B.
B.
?
C.
D.
5、(2019?碑林区校级模拟)如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD,AE,则∠EAD的度数为( C )
A.150°
B.135°
C.120°
D.105°
6、如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是(
B
)
A.1.4
B.
C.5/2
D.2.6
7、如图,⊙A过点O(0,0),C(),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,
则∠OBD的度数是(
B
)
A、15°
B、30°
C、45°
D、60°
8、如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,
则线段CP长的最小值为(
B
)
A、
B、2
C、
D、
9、直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是(C )
A.r<6
B.r=6
C.r>6
D.r≥6
10、如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,
则弦长AB的取值范围是_C___
A.8≤AB≤10
B.AB≥8
C.8<AB≤10
D.8<AB<10
二、填空题
11、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
上
,点B在⊙C
外
.
12、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
11.3
13、(2019秋?海陵区校级期末)如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH=6,则BG+DF为
.
【分析】作OM⊥GH于M,OM交EF于N,如图,先证明OM⊥EF,利用垂径定理得到EN=FN,GM=HM,利用四边形ABMN和四边形MNDC为矩形得到AN=BM,DN=CM,然后根据等线段代换得到BG+DF=AE+CH.
【解答】解:作OM⊥GH于M,OM交EF于N,如图,
∵EF∥GH,∴OM⊥EF,∴EN=FN,GM=HM,
易得四边形ABMN和四边形MNDC为矩形,∴AN=BM,DN=CM,
∴BG+DF=BM﹣GM+DN﹣NF=AN﹣HM+CM﹣EN=AN﹣EN+CM﹣HM=AE+CH=6.
故答案为6.
14、如图,是的直径,,交于点,交于点,,给出下列五个结论:①;②;③;④劣弧是劣弧的倍;⑤.
其中正确结论的序号是________.
【答案】①②④
15、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为,
则该圆弧所在圆的圆心坐标为______.
16、如图,线段,点从点出发沿向点匀速运动,速度为,同时点?从点出发沿向点以相同速度运动,以点为圆心,长为半径作,点到达点时也停止运动,设运动时间为秒,则点在内部时的取值范围是________.
17、(2019秋?吴中区期中)如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE,若∠B=76°,则∠AEC= 104 °.
【分析】根据平行四边形的性质求出∠D,根据圆内接四边形的性质得出∠D+∠AEC=180°,代入求出即可.
【解析】∵四边形ABCD是平行四边形,∠B=76°,
∴∠D=∠B=76°,
∵四边形AECD是⊙O的内接四边形,
∴∠D+∠AEC=180°,
∴∠AEC=180°﹣76°=104°,
故答案为:104.
18、如图,AB是⊙O的直径,点C、D、E都在⊙O上,若∠C=∠D=∠E,则∠A+∠B=__135____°
19、在△ABC中,点I是内心,若∠A=80°,则∠DEF=________度.
解:连接IF,ID,
∵点I是内心,∴∠ADI=∠AFI=90°,
∵∠A=80°,∴∠DIF=100°,∴∠DEF=50°,故答案为:50.
20、(2019秋?建邺区期中)如图,△ABC为等边三角形,AB=4,以点A为圆心,半径为1作⊙A.M为BC边上的一动点,过点M作⊙A的一条切线,切点为N,则MN的最小值是 .
【分析】作AD⊥BC于D,过D作⊙A的一条切线,切点为E,连接AE,由等边三角形的性质和勾股定理得出AD2,由切线的性质得出AE⊥DE,由勾股定理求出DE,当点M与D重合时,N与E重合,此时MN最小.
【解析】作AD⊥BC于D,过D作⊙A的一条切线,切点为E,连接AE,如图所示:
∵△ABC是等边三角形,AD⊥BC,
∴BC=AB=4,BD=CDBC=2,
∴AD2,
∵DE是⊙A的一条切线,
∴AE⊥DE,AE=1,
∴DE,
当点M与D重合时,N与E重合,
此时MN最小,
故答案为:.
三、解答题
21、Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.
证明:(Ⅰ)连接OE,BD,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=90°,
∵E点是BC的中点,∴DE=BC=BE,
∵OD=OB,OE=OE,∴△ODE≌△OBE,∴∠ODE=∠OBE,
∵∠ABC=90°,∴∠ODE=90°;
(Ⅱ)∵CF=OF,CE=EB,∴FE是△COB的中位线,∴FE∥OB,∴∠AOD=∠ODE,
由(Ⅰ)得∠ODE=90°,∴∠AOD=90°,
∵OA=OD,∴∠A=∠ADO=.
22、如图,的直径,是线段的中点.
试判断点与的位置关系,并说明理由;?
过点作,垂足为点,求证直线是的切线.
解:点与的位置关系是在上,
理由是:
设交于,连接,
∵为的直径,∴,
∵,,∴,由勾股定理得:,
∵,为的中点,∴,即、互相重合,∴在上;
(2)
证明:连接,
∵为的中点,,∴,
∵,∴,∵为半径,∴直线是的切线.
23、如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
【答案】
(1)证明:连接OB,
∵OA=OB,DC=DB,∴∠A=∠ABO,∠DCB=∠DBC,
∵AO⊥OD,∴∠AOC=90°,即∠A+∠ACO=90°,
∵∠ACO=∠DCB=∠DBC,∴∠ABO+∠DBC=90°,即OB⊥BD,则BD为圆O的切线;
(2)解:设BD=x,则OD=x+1,而OB=OA=3,
在RT△OBD中,OB2+BD2=OD2
,
即32+x2=(x+1)2
,
解得x=4,∴线段BD的长是4.
?
24、如图,在中,,以AC为直径的与AB交于点D,过点D作的切线
交BC于点E.
(1)求证:;
(2)填空:若,,则________;
当________时,以O,D,E,C为顶点的四边形是正方形.
证明:连接DO.
,AC为直径,为的切线;
又也为的切线,,
又,,
又,,,;
解:,,,,
,
为直径,,
由得:,,故答案为3;
当时,四边形ODEC是正方形,理由如下:
,,
,,,,
,四边形DECO是矩形,
,矩形DECO是正方形.
25、(2019?姑苏区校级二模)如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.
(1)求证:EC是圆O的切线;
(2)当∠ABC=22.5°时,连接CF,
①求证:AC=CF;
②若AD=1,求线段FG的长.
【分析】(1)连接OC,证得OC⊥CE,即可证得结论;
(2)①通过证得∠AOC=45°=∠COF=45°,得出,即可证得AC=CF;
②作CM⊥OE于M,首先证得CF=CG,得出CM垂直平分FG,然后通过三角形平分线的性质证得CM=CD,即可证得Rt△ACD≌Rt△FCM,从而证得FM=AD=1,即可证得FG=2FM=2.
【答案】(1)证明:连接OC,
∵OC=OB,∴∠OCB=∠B,
∵EO⊥AB,∴∠OGB+∠B=90°,
∵EG=EC,∴∠ECG=∠EGC,
∵∠EGC=∠OGB,∴∠OCB+∠ECG=∠B+∠OGB=90°,∴OC⊥CE,
∴EC是圆O的切线;
(2)①证明:∵∠ABC=22.5°,∠OCB=∠B,∴∠AOC=45°,
∵EO⊥AB,∴∠COF=45°,∴,∴AC=CF;
②解:作CM⊥OE于M,
∵AB为直径,∴∠ACB=90°
∵∠ABC=22.5°,∠GOB=90°,∴∠A=∠OGB=∠67.5°,∴∠FGC=67.5°,
∵∠COF=45°,OC=OF,∴∠OFC=∠OCF=67.5°,∴∠GFC=∠FGC,
∴CF=CG,∴FM=GM,
∵∠AOC=∠COF,CD⊥OA,CM⊥OF,∴CD=DM,
在Rt△ACD和Rt△FCM中
∴Rt△ACD≌Rt△FCM(HL),∴FM=AD=1,∴FG=2FM=2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
