华东师大版九年级上册 数学 23.1.2平行线分线段成比例 课件 (19张PPT)
文档属性
| 名称 | 华东师大版九年级上册 数学 23.1.2平行线分线段成比例 课件 (19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 347.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 15:47:08 | ||
图片预览





文档简介
(共19张PPT)
平行线分线段成比例
相似多边形
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
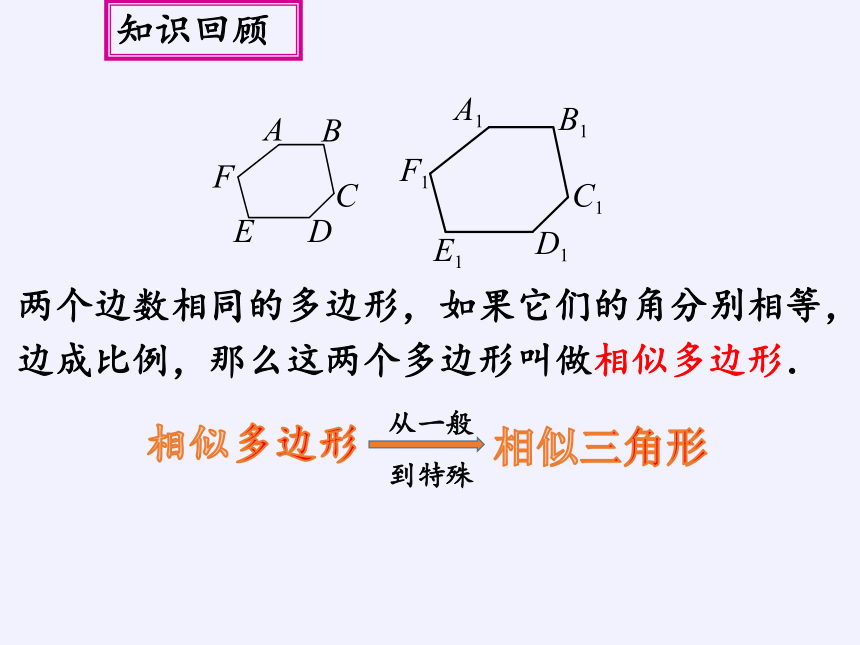
两个边数相同的多边形,如果它们的角分别相等,
边成比例,那么这两个多边形叫做相似多边形.
相似三角形
知识回顾
从一般
到特殊
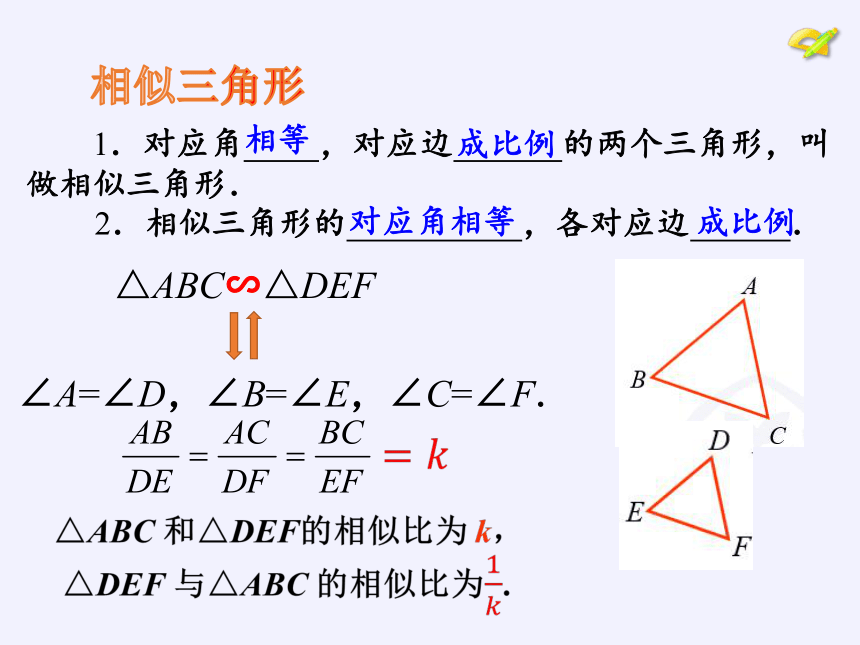
1.对应角
,对应边
的两个三角形,叫做相似三角形.
相等
成比例
对应角相等
成比例
∠A=∠D,∠B=∠E,∠C=∠F.
△ABC∽△DEF
2.相似三角形的
,各对应边
.
相似三角形
?
创设情境,引入新知
问题1:任意画一个等边三角形,请同学们分别画和它相似的等边三角形,所画的图和该图的
相似比k为1:2,1:4,3:4.
k为1:4
平行
线段成比例
相似
等边三角形
角相等
创设情境,引入新知
问题2:平行线具有截等角的功能,那么在一般图形中,你能否进行更大胆、更惊艳的猜想,平行线还有什么功能?
k为1:4
平行
线段成比例
相似
等边三角形
角相等
实践感悟,探究定理
任意画两条直线m,n,再画三条与m、n都相交的平行线,将l1,l2,l3在直线
m,n上截得的分线段记为a,b,c,d,探究这四条线段成比例.
小组交流讨论
问题3:对于一般的情况,你有什么办法
说明猜想的合理性?
实践感悟,探究定理
几何画板验算
?
l1
l2
l3
实践感悟,探究定理
除了
还有其它线段的比相等吗?
你能用简洁的文字语言来叙述上面所得到的结论吗?
…
平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
实践感悟,探究定理
…
对应线段是指一条直线被两条平行直线截得的线段与另一条直线被两条平行直线截得的线段对应.
问题:请同学们以这个图形为基础,改变截线m,n的相对位置关系,使得这个基本事实运用到三角形中.
拓广分析,特例提升
问题:请同学们以这个图形为基础,改变截线m,n的相对位置关系,使得这个基本事实运用到三角形中.
拓广分析,特例提升
A
B
C
(D)
E
F
l1
l2
l3
m
n
问题:请同学们以这个图形为基础,改变截线m,n的相对位置关系,使得这个基本事实运用到三角形中.
拓广分析,特例提升
A
B
C
D
(E)
F
l1
l2
l3
m
n
拓广分析,特例提升
A
B
C
D
(E)
F
l1
l2
l3
m
n
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
应用迁移,巩固提高
(课本
P31第1题)如图,AB∥CD∥EF,
AF与BE相交于点G,且AG=2,GD=1,
DF=5,求
的值.
应用迁移,巩固提高
2.如图,DE∥AF∥BC,找出图中的成比例线段.
畅所欲言
问题1:这节课你学习了什么?
问题2:回顾探究平行线分线段成比例基本事实的过程,我们是怎么探究的?
?
问题3:当平行线处于特殊位置(中位线)时,
你发现了什么?
如果平行线DE不是在中位线的位置,还会相似吗?
畅所欲言
从特殊
到一般
?
必做:完成校本作业.
选做:除平行线分线段成比例基本事实的推论外,你还能想出其他拓广情况或特殊情形吗?
作业
谢
谢
平行线分线段成比例
相似多边形
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
两个边数相同的多边形,如果它们的角分别相等,
边成比例,那么这两个多边形叫做相似多边形.
相似三角形
知识回顾
从一般
到特殊
1.对应角
,对应边
的两个三角形,叫做相似三角形.
相等
成比例
对应角相等
成比例
∠A=∠D,∠B=∠E,∠C=∠F.
△ABC∽△DEF
2.相似三角形的
,各对应边
.
相似三角形
?
创设情境,引入新知
问题1:任意画一个等边三角形,请同学们分别画和它相似的等边三角形,所画的图和该图的
相似比k为1:2,1:4,3:4.
k为1:4
平行
线段成比例
相似
等边三角形
角相等
创设情境,引入新知
问题2:平行线具有截等角的功能,那么在一般图形中,你能否进行更大胆、更惊艳的猜想,平行线还有什么功能?
k为1:4
平行
线段成比例
相似
等边三角形
角相等
实践感悟,探究定理
任意画两条直线m,n,再画三条与m、n都相交的平行线,将l1,l2,l3在直线
m,n上截得的分线段记为a,b,c,d,探究这四条线段成比例.
小组交流讨论
问题3:对于一般的情况,你有什么办法
说明猜想的合理性?
实践感悟,探究定理
几何画板验算
?
l1
l2
l3
实践感悟,探究定理
除了
还有其它线段的比相等吗?
你能用简洁的文字语言来叙述上面所得到的结论吗?
…
平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
实践感悟,探究定理
…
对应线段是指一条直线被两条平行直线截得的线段与另一条直线被两条平行直线截得的线段对应.
问题:请同学们以这个图形为基础,改变截线m,n的相对位置关系,使得这个基本事实运用到三角形中.
拓广分析,特例提升
问题:请同学们以这个图形为基础,改变截线m,n的相对位置关系,使得这个基本事实运用到三角形中.
拓广分析,特例提升
A
B
C
(D)
E
F
l1
l2
l3
m
n
问题:请同学们以这个图形为基础,改变截线m,n的相对位置关系,使得这个基本事实运用到三角形中.
拓广分析,特例提升
A
B
C
D
(E)
F
l1
l2
l3
m
n
拓广分析,特例提升
A
B
C
D
(E)
F
l1
l2
l3
m
n
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
应用迁移,巩固提高
(课本
P31第1题)如图,AB∥CD∥EF,
AF与BE相交于点G,且AG=2,GD=1,
DF=5,求
的值.
应用迁移,巩固提高
2.如图,DE∥AF∥BC,找出图中的成比例线段.
畅所欲言
问题1:这节课你学习了什么?
问题2:回顾探究平行线分线段成比例基本事实的过程,我们是怎么探究的?
?
问题3:当平行线处于特殊位置(中位线)时,
你发现了什么?
如果平行线DE不是在中位线的位置,还会相似吗?
畅所欲言
从特殊
到一般
?
必做:完成校本作业.
选做:除平行线分线段成比例基本事实的推论外,你还能想出其他拓广情况或特殊情形吗?
作业
谢
谢
