人教版(五四制)初中数学九年级上册30.1 图形的旋转 课件(30张)
文档属性
| 名称 | 人教版(五四制)初中数学九年级上册30.1 图形的旋转 课件(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 965.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 14:11:44 | ||
图片预览









文档简介
(共30张PPT)
图形的旋转
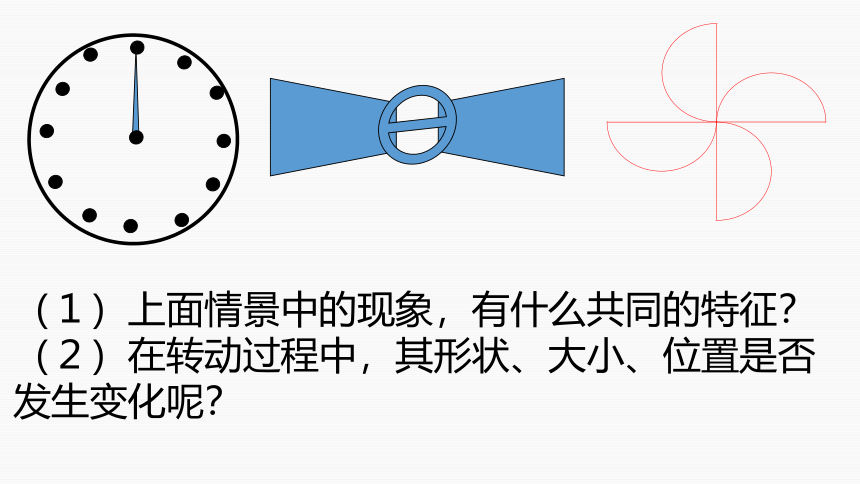
石英钟的指针是怎样走动的呢?
情景导入
电扇启动后,它的叶子是怎么样转动的呢?
大风车迎风而动,它是怎么转动的?
(1)上面情景中的现象,有什么共同的特征?
(2)在转动过程中,其形状、大小、位置是否发生变化呢?
将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转角α),得到图形F',如图,图形的这种变换叫做旋转.这个定点
O
叫旋转中心,角α叫做旋转角.
原位置的图形F
叫做原像,新位置的图形F'叫做图形F在旋转下的像.
图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.
图5-10
推进新课
结合图形看概念
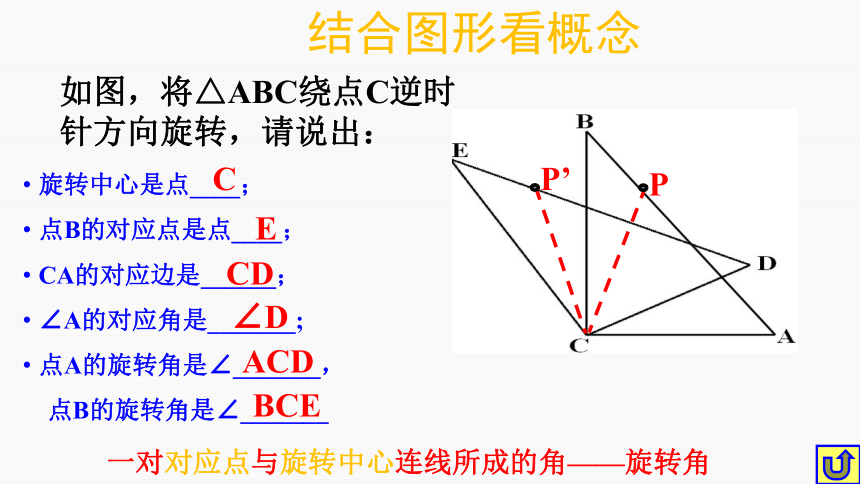
如图,将△ABC绕点C逆时针方向旋转,请说出:
旋转中心是点____;
点B的对应点是点____;
CA的对应边是______;
∠A的对应角是_______;
点A的旋转角是∠_______,
点B的旋转角是∠_______
C
E
CD
∠D
一对对应点与旋转中心连线所成的角——旋转角
ACD
P
P’
BCE
知识点
1
图形的旋转?
如图,如果把钟表的指针看作四边形AOBC,它绕O点旋转得到四边形DOEF(旋转角度不大于180°).在这个旋转过程中:
(1)旋转中心是哪一点?
(2)指出旋转方向.
(3)请指出点A,B,C的对应点.
(4)指出线段AO,BO,AC,BC的对应线段.
(5)指出∠A,∠B,∠C的对应角.
(6)旋转角是什么?(用三个字母表示)
思考:(1)如何识别旋转中心?
(2)如何找点A,B,C的对应点?
【方法小窍门】
(1)如何识别旋转中心?
提示:旋转图形中的不动点即为旋转中心.即点O为旋转中心.
(2)点A,B,C经过旋转后的对应点是什么?
提示:点A与点D重合,点B与点E重合,点C与点F重合;所以点A,B,C的对应点是点D,E,F.
(3)如何寻找旋转角?
提示:对应点与旋转中心的连线(如AO和DO)所成的夹角(∠AOD)
(4)图形的旋转有几种旋转方向?
提示:图形的旋转一般有顺时针和逆时针两种;本题的旋转方向为顺时针.
【总结提升】
1.旋转中心:旋转中心是点而不是直线,比如生活中的开门、关门,虽然门转动了,但它是绕轴旋转一定的角度,所以不属于我们要研究的绕定点旋转.
2.旋转方向:旋转方向通常指顺时针方向或逆时针方向.
3.旋转角:因为经过旋转,图形上每一个点都绕旋转中心沿相同的方向转动了相同的角度,所以任意一对对应点与旋转中心的连线所成的角都是旋转角,不要把图形中的某些对应角误以为是旋转角.
知识点
2
旋转的三个要素
(打“√”或“×”)
(1)图形的旋转是由旋转中心决定的.(
)
(2)图形的旋转过程中,旋转中心是保持不动的.(
)
(3)旋转中心不同,旋转后图形的形状就不同.(
)
(4)正方形旋转90°后能与原来的正方形重合.(
)
(5)旋转的原象与象的对应点到旋转中心的距离相等.(
)
×
√
×
×
√
结论
一般地,旋转具有下述性质:
(1)对应点到旋转中心的距离相等。
(2)各组对应点与旋转中心的连线所成的角相等,都等于旋转角。
(3)旋转中心是唯一不动的点。
(4)旋转不改变图形的大小和形状。(对应角相等,对应线段相等)
知识点
3
旋转的基本性质
A
O
点的旋转作法
1、将A点绕O点沿顺时针方向旋转60?.
作法:
1.
以点O为圆心,OA长为半径画圆;
2.
连接OA,
用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3.
B点即为所求作.
B
知识点
4
简单的旋转作图
A
O
线段的旋转作法
2、将线段AB绕O点沿顺时针方向旋转60?.
作法:
将点A绕点O顺时针旋转60?,得
点A';
2.
将点B绕点O顺时针旋转60
?,得点B'
;
3.
连接A'B',
则线段A'B'即为所求作.
A’
B
B'
图形的旋转作法
3、
如图,△ABC绕C点旋转后,顶点A得对应点为点D.
试确定顶点B对应点的位置以及旋转后的三角形.
作法一:
1.
连接CD;
2.
以CB为一边,作∠BCE,使得∠BCE=∠ACD
;
3.
在射线CB上截取CE,使得CE=CB;
4.
连接DE,则△DEC即为所求作.
C
A
B
D
思路:
关键:
反思:如何画图?
转
化
点旋转
形旋转
作确定图形点的对应点。
课堂小结
通过这节课的学习活动,你学到了什么新知识?
图形的旋转
旋转前后图形全等
线:每对对应点与旋转中心的距离相等
角:旋转角彼此相等
思路:形旋转
点旋转
3、作图
关键:作确定图形点的对应点。
对应线段相等
对应角相等
转化
2、性质
1、定义
一个定点
(旋转中心)
某个方向
(旋转方向)
一定的角度
(旋转角)
1.将图(1)按顺时针方向旋转90°后得到的是( )
【解析】选A.根据旋转的性质,图(1)按顺时针方向旋转90°,应为选项A.
2.下列运动属于旋转的是( )
A.滚动过程中的篮球
B.钟表的钟摆的摆动
C.气球升空的运动
D.一个图形沿某直线对折的过程
【解析】选B.A选项滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B选项钟表的钟摆的摆动,符合旋转的定义,属于旋转;C选项气球升空的运动不属于旋转;D选项一个图形沿某直线对折的过程是轴对称,不属于旋转.
3.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经逆时针
旋转后到达△CAE的位置,则旋转中心是点 ;旋转角度
是 ;点B的对应点是点 ;点D的对应点是点
;线段CB的对应线段是 ;∠B的对应角是
.
4.如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,
△ABD绕点A旋转后得到△ACE,则CE的长度为 .
课堂训练——能力提升
5.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB
'的度数是
(
)
A.25°
B.30°
C.35°
D.40°
解析
由旋转的性质应选B.
【想一想错在哪?】如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A'B'C的位置,则旋转角的度数是多少度?
6.如图所示,在正方形网格中,图①经过 变换可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点
(填“A”“B”或“C”).
右图可以看做是一个或几个菱形通
过多次旋转得到的。
由一个菱形通过6次旋转得到,每次旋转60度。
转一转
综合运用
由两个菱形旋转3次得到,
每次旋转120度。
由三个菱形旋转2次得到,
旋转180度。
转一转
1.从教材课后习题中选取(抽查);
2.完成《全效学习》本课时的习题(上交)。
课后作业
欣
赏
平移
翻折
①
②
③
④
⑤
⑥
⑦
⑧
⑨
平移
翻折
翻折
平移
课后提升
o
C
B
D
A
图形变换的“家族”
3、平移和旋转的异同:
①、相同:都是一种运动;运动前后不改变图形的
形状和大小
B
A
C
O
②、不同
图形变换
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或
逆时针
转动一定的角度
图形的旋转
石英钟的指针是怎样走动的呢?
情景导入
电扇启动后,它的叶子是怎么样转动的呢?
大风车迎风而动,它是怎么转动的?
(1)上面情景中的现象,有什么共同的特征?
(2)在转动过程中,其形状、大小、位置是否发生变化呢?
将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转角α),得到图形F',如图,图形的这种变换叫做旋转.这个定点
O
叫旋转中心,角α叫做旋转角.
原位置的图形F
叫做原像,新位置的图形F'叫做图形F在旋转下的像.
图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.
图5-10
推进新课
结合图形看概念
如图,将△ABC绕点C逆时针方向旋转,请说出:
旋转中心是点____;
点B的对应点是点____;
CA的对应边是______;
∠A的对应角是_______;
点A的旋转角是∠_______,
点B的旋转角是∠_______
C
E
CD
∠D
一对对应点与旋转中心连线所成的角——旋转角
ACD
P
P’
BCE
知识点
1
图形的旋转?
如图,如果把钟表的指针看作四边形AOBC,它绕O点旋转得到四边形DOEF(旋转角度不大于180°).在这个旋转过程中:
(1)旋转中心是哪一点?
(2)指出旋转方向.
(3)请指出点A,B,C的对应点.
(4)指出线段AO,BO,AC,BC的对应线段.
(5)指出∠A,∠B,∠C的对应角.
(6)旋转角是什么?(用三个字母表示)
思考:(1)如何识别旋转中心?
(2)如何找点A,B,C的对应点?
【方法小窍门】
(1)如何识别旋转中心?
提示:旋转图形中的不动点即为旋转中心.即点O为旋转中心.
(2)点A,B,C经过旋转后的对应点是什么?
提示:点A与点D重合,点B与点E重合,点C与点F重合;所以点A,B,C的对应点是点D,E,F.
(3)如何寻找旋转角?
提示:对应点与旋转中心的连线(如AO和DO)所成的夹角(∠AOD)
(4)图形的旋转有几种旋转方向?
提示:图形的旋转一般有顺时针和逆时针两种;本题的旋转方向为顺时针.
【总结提升】
1.旋转中心:旋转中心是点而不是直线,比如生活中的开门、关门,虽然门转动了,但它是绕轴旋转一定的角度,所以不属于我们要研究的绕定点旋转.
2.旋转方向:旋转方向通常指顺时针方向或逆时针方向.
3.旋转角:因为经过旋转,图形上每一个点都绕旋转中心沿相同的方向转动了相同的角度,所以任意一对对应点与旋转中心的连线所成的角都是旋转角,不要把图形中的某些对应角误以为是旋转角.
知识点
2
旋转的三个要素
(打“√”或“×”)
(1)图形的旋转是由旋转中心决定的.(
)
(2)图形的旋转过程中,旋转中心是保持不动的.(
)
(3)旋转中心不同,旋转后图形的形状就不同.(
)
(4)正方形旋转90°后能与原来的正方形重合.(
)
(5)旋转的原象与象的对应点到旋转中心的距离相等.(
)
×
√
×
×
√
结论
一般地,旋转具有下述性质:
(1)对应点到旋转中心的距离相等。
(2)各组对应点与旋转中心的连线所成的角相等,都等于旋转角。
(3)旋转中心是唯一不动的点。
(4)旋转不改变图形的大小和形状。(对应角相等,对应线段相等)
知识点
3
旋转的基本性质
A
O
点的旋转作法
1、将A点绕O点沿顺时针方向旋转60?.
作法:
1.
以点O为圆心,OA长为半径画圆;
2.
连接OA,
用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3.
B点即为所求作.
B
知识点
4
简单的旋转作图
A
O
线段的旋转作法
2、将线段AB绕O点沿顺时针方向旋转60?.
作法:
将点A绕点O顺时针旋转60?,得
点A';
2.
将点B绕点O顺时针旋转60
?,得点B'
;
3.
连接A'B',
则线段A'B'即为所求作.
A’
B
B'
图形的旋转作法
3、
如图,△ABC绕C点旋转后,顶点A得对应点为点D.
试确定顶点B对应点的位置以及旋转后的三角形.
作法一:
1.
连接CD;
2.
以CB为一边,作∠BCE,使得∠BCE=∠ACD
;
3.
在射线CB上截取CE,使得CE=CB;
4.
连接DE,则△DEC即为所求作.
C
A
B
D
思路:
关键:
反思:如何画图?
转
化
点旋转
形旋转
作确定图形点的对应点。
课堂小结
通过这节课的学习活动,你学到了什么新知识?
图形的旋转
旋转前后图形全等
线:每对对应点与旋转中心的距离相等
角:旋转角彼此相等
思路:形旋转
点旋转
3、作图
关键:作确定图形点的对应点。
对应线段相等
对应角相等
转化
2、性质
1、定义
一个定点
(旋转中心)
某个方向
(旋转方向)
一定的角度
(旋转角)
1.将图(1)按顺时针方向旋转90°后得到的是( )
【解析】选A.根据旋转的性质,图(1)按顺时针方向旋转90°,应为选项A.
2.下列运动属于旋转的是( )
A.滚动过程中的篮球
B.钟表的钟摆的摆动
C.气球升空的运动
D.一个图形沿某直线对折的过程
【解析】选B.A选项滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B选项钟表的钟摆的摆动,符合旋转的定义,属于旋转;C选项气球升空的运动不属于旋转;D选项一个图形沿某直线对折的过程是轴对称,不属于旋转.
3.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经逆时针
旋转后到达△CAE的位置,则旋转中心是点 ;旋转角度
是 ;点B的对应点是点 ;点D的对应点是点
;线段CB的对应线段是 ;∠B的对应角是
.
4.如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,
△ABD绕点A旋转后得到△ACE,则CE的长度为 .
课堂训练——能力提升
5.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB
'的度数是
(
)
A.25°
B.30°
C.35°
D.40°
解析
由旋转的性质应选B.
【想一想错在哪?】如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A'B'C的位置,则旋转角的度数是多少度?
6.如图所示,在正方形网格中,图①经过 变换可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点
(填“A”“B”或“C”).
右图可以看做是一个或几个菱形通
过多次旋转得到的。
由一个菱形通过6次旋转得到,每次旋转60度。
转一转
综合运用
由两个菱形旋转3次得到,
每次旋转120度。
由三个菱形旋转2次得到,
旋转180度。
转一转
1.从教材课后习题中选取(抽查);
2.完成《全效学习》本课时的习题(上交)。
课后作业
欣
赏
平移
翻折
①
②
③
④
⑤
⑥
⑦
⑧
⑨
平移
翻折
翻折
平移
课后提升
o
C
B
D
A
图形变换的“家族”
3、平移和旋转的异同:
①、相同:都是一种运动;运动前后不改变图形的
形状和大小
B
A
C
O
②、不同
图形变换
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或
逆时针
转动一定的角度
