人教版八年级上册数学课件:12.2.3全等三角形的判定(1)——边角边(16张)
文档属性
| 名称 | 人教版八年级上册数学课件:12.2.3全等三角形的判定(1)——边角边(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:18:42 | ||
图片预览



文档简介
(共17张PPT)
全等三角形的判定(1)——边角边
泸化中学
学习目标
1.知识与技能
会用“S.A.S”识别两三角形全等;正确使用两三角形的全等来证明两线段相等,两个角相等。
2.过程与方法
在探索三角形全等判定定理的过程中,体会提出判定定理的必要性。
3.情感态度与价值观
通过三角形全等判定定理的证明与使用,培养自己严密的逻辑思维。
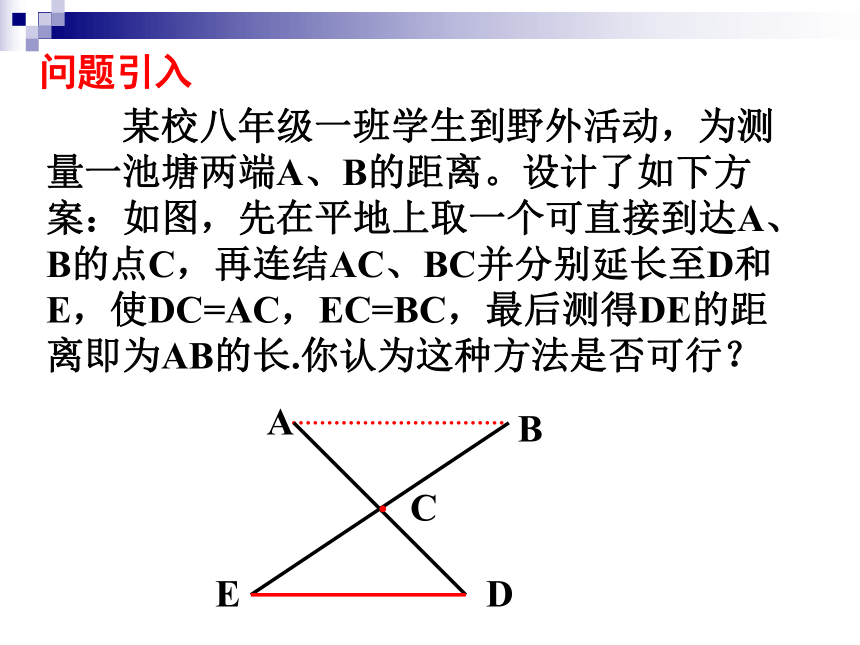
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长至D和E,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
·
A
E
D
B
问题引入
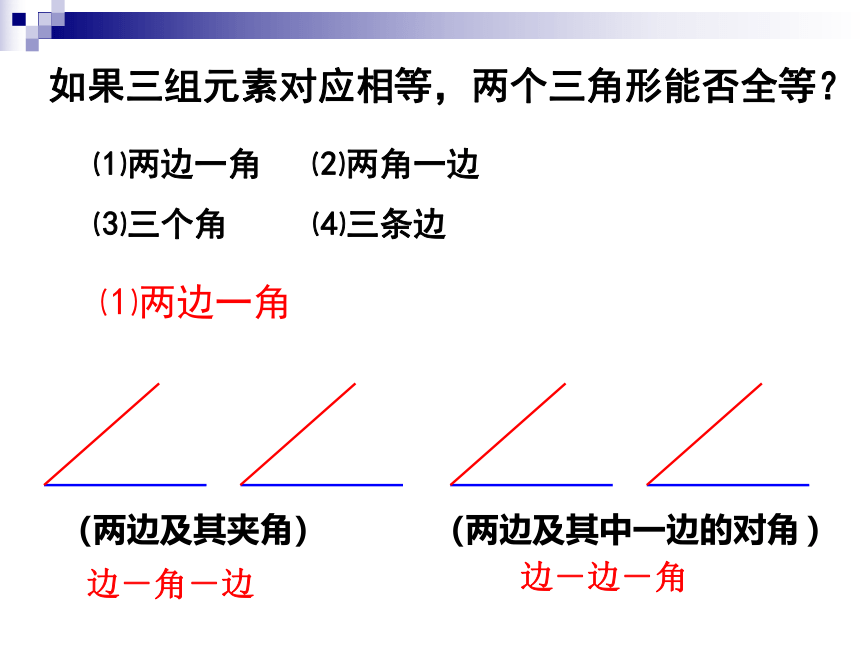
⑴两边一角
⑵两角一边
⑶三个角
⑷三条边
边-角-边
边-边-角
(两边及其夹角)
(两边及其中一边的对角
)
如果三组元素对应相等,两个三角形能否全等?
⑴两边一角
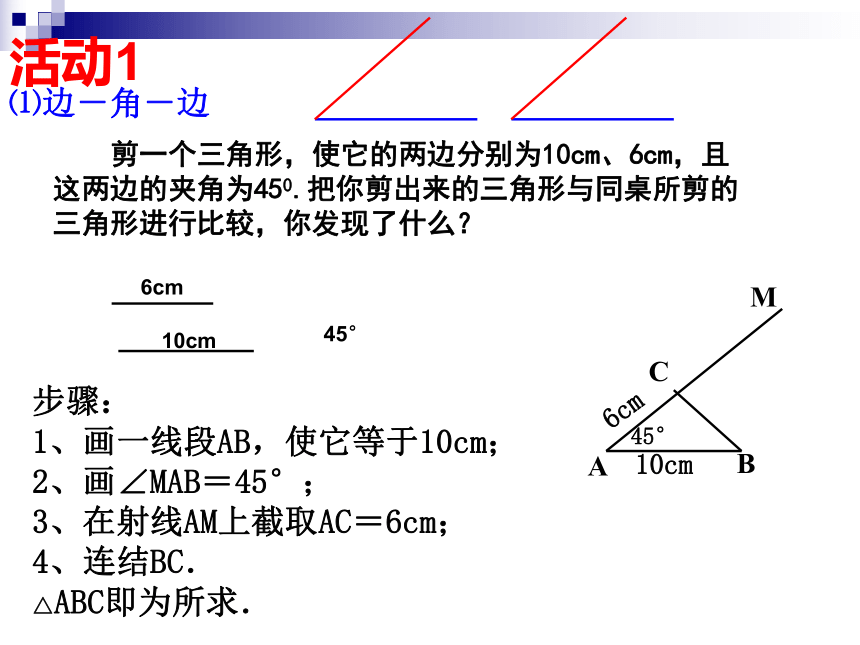
活动1
⑴边-角-边
剪一个三角形,使它的两边分别为10cm、6cm,且这两边的夹角为450.把你剪出来的三角形与同桌所剪的三角形进行比较,你发现了什么?
6cm
10cm
45°
步骤:
1、画一线段AB,使它等于10cm;
2、画∠MAB=45°;
3、在射线AM上截取AC=6cm;
4、连结BC.
△ABC即为所求.
A
B
M
C
10cm
45°
6cm
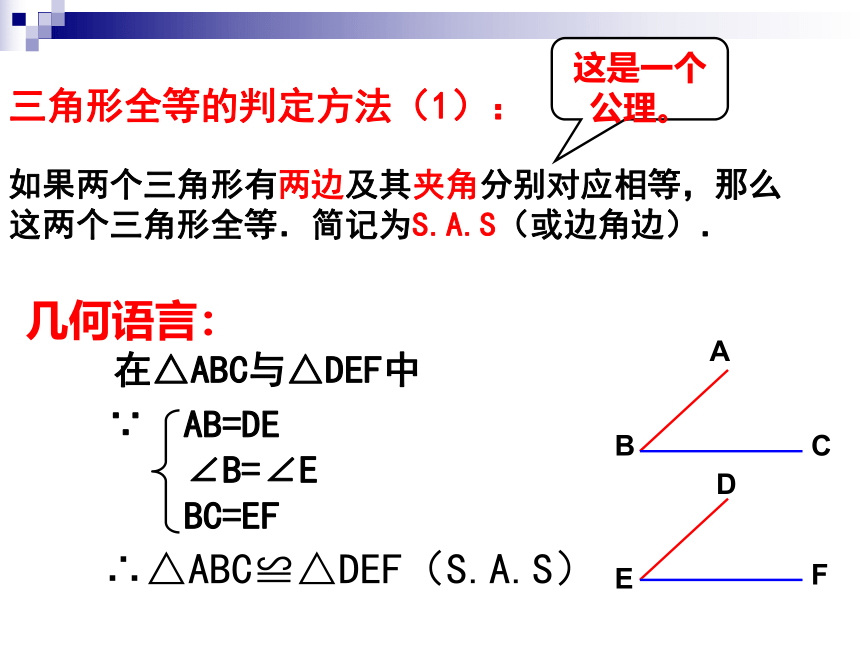
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简记为S.A.S(或边角边).
三角形全等的判定方法(1):
几何语言:
在△ABC与△DEF中
A
B
C
D
E
F
∴△ABC≌△DEF(S.A.S)
这是一个公理。
∵
AB=DE
∠B=∠E
BC=EF
活动2
⑵边-边-角
剪一个三角形,使它的两边长分别为6cm、10cm,且6cm所对的角为45°,情况又怎样?
6cm
10cm
45°
步骤:
1、画一线段AB,使它等于10cm
;
2、画∠
BAM=
45°
;
3、以B为圆心,
6cm长为半径画弧,
交AM于点C
;
4、连结CB
.
△ABC即为所求.
A
B
M
C
D
结论:两边及其一边所对的角相等,两
个三角形不一定全等.
A
B
C
A
B
D
10cm
6cm
6cm
例1:如图19.2.4,在△ABC中,AB=AC,
AD平分∠BAC,求证:△ABD≌△ACD.
证明:
∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
∴△ABD≌△ACD(S.A.S.)
∵
AB=AC
∠BAD=∠CAD
AD=AD
巩固练习
1.如图所示,根据题目条件,判断下面的三角形是否全等.
⑴ AC=DF, ∠C=∠F, BC=EF;
⑵
BC=BD, ∠ABC=∠ABD.
⑶
AD=CB,
DF=BE,
∠DAF=∠BCE
答:
(1)全等
(2)全等
F
A
B
D
C
E
⑶不一定全等
⑶
2.点M是等腰梯形ABCD底边AB的
中点,求证:⑴△AMD≌△BMC
⑵DM=CM,∠ADM=∠BCM.
证明:
⑴
∵ 点M是等腰梯形ABCD底边AB的中点
∴ AD=BC
,∠A=∠B,AM=BM
在△ADM和△BCM中
∴△AMD≌△BMC
(S.A.S)
∴
DM=CM,∠ADM=∠BCM
∵
AD=BC
∠A=∠B
AM=BM
⑵
∵
△AMD≌△BMC
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长至D和E,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
A
E
D
B
问题回顾:
在△DCE和△ACB中
∵
DC=AC
∠DCE=∠ACB
EC=BC
∴△DCE≌△ACB(S.A.S)
∴DE=AB
解:
www.czsx.com.cn
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
畅所欲言
作业:
P79习题19.2
第
2、4题
P96复习题
第4题
谢
谢
全等三角形的判定(1)——边角边
泸化中学
学习目标
1.知识与技能
会用“S.A.S”识别两三角形全等;正确使用两三角形的全等来证明两线段相等,两个角相等。
2.过程与方法
在探索三角形全等判定定理的过程中,体会提出判定定理的必要性。
3.情感态度与价值观
通过三角形全等判定定理的证明与使用,培养自己严密的逻辑思维。
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长至D和E,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
·
A
E
D
B
问题引入
⑴两边一角
⑵两角一边
⑶三个角
⑷三条边
边-角-边
边-边-角
(两边及其夹角)
(两边及其中一边的对角
)
如果三组元素对应相等,两个三角形能否全等?
⑴两边一角
活动1
⑴边-角-边
剪一个三角形,使它的两边分别为10cm、6cm,且这两边的夹角为450.把你剪出来的三角形与同桌所剪的三角形进行比较,你发现了什么?
6cm
10cm
45°
步骤:
1、画一线段AB,使它等于10cm;
2、画∠MAB=45°;
3、在射线AM上截取AC=6cm;
4、连结BC.
△ABC即为所求.
A
B
M
C
10cm
45°
6cm
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简记为S.A.S(或边角边).
三角形全等的判定方法(1):
几何语言:
在△ABC与△DEF中
A
B
C
D
E
F
∴△ABC≌△DEF(S.A.S)
这是一个公理。
∵
AB=DE
∠B=∠E
BC=EF
活动2
⑵边-边-角
剪一个三角形,使它的两边长分别为6cm、10cm,且6cm所对的角为45°,情况又怎样?
6cm
10cm
45°
步骤:
1、画一线段AB,使它等于10cm
;
2、画∠
BAM=
45°
;
3、以B为圆心,
6cm长为半径画弧,
交AM于点C
;
4、连结CB
.
△ABC即为所求.
A
B
M
C
D
结论:两边及其一边所对的角相等,两
个三角形不一定全等.
A
B
C
A
B
D
10cm
6cm
6cm
例1:如图19.2.4,在△ABC中,AB=AC,
AD平分∠BAC,求证:△ABD≌△ACD.
证明:
∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
∴△ABD≌△ACD(S.A.S.)
∵
AB=AC
∠BAD=∠CAD
AD=AD
巩固练习
1.如图所示,根据题目条件,判断下面的三角形是否全等.
⑴ AC=DF, ∠C=∠F, BC=EF;
⑵
BC=BD, ∠ABC=∠ABD.
⑶
AD=CB,
DF=BE,
∠DAF=∠BCE
答:
(1)全等
(2)全等
F
A
B
D
C
E
⑶不一定全等
⑶
2.点M是等腰梯形ABCD底边AB的
中点,求证:⑴△AMD≌△BMC
⑵DM=CM,∠ADM=∠BCM.
证明:
⑴
∵ 点M是等腰梯形ABCD底边AB的中点
∴ AD=BC
,∠A=∠B,AM=BM
在△ADM和△BCM中
∴△AMD≌△BMC
(S.A.S)
∴
DM=CM,∠ADM=∠BCM
∵
AD=BC
∠A=∠B
AM=BM
⑵
∵
△AMD≌△BMC
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长至D和E,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
A
E
D
B
问题回顾:
在△DCE和△ACB中
∵
DC=AC
∠DCE=∠ACB
EC=BC
∴△DCE≌△ACB(S.A.S)
∴DE=AB
解:
www.czsx.com.cn
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
畅所欲言
作业:
P79习题19.2
第
2、4题
P96复习题
第4题
谢
谢
