人教版七年级数学上册课件:3.1.2等式的性质(共22张PPT)
文档属性
| 名称 | 人教版七年级数学上册课件:3.1.2等式的性质(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
3.1.2
等式的性质
等
式
性
质
什么是方程?
方程是含有
______的____。
2.
指出下列式子中哪些是方程,哪些不是,并说明为什么?
3
+
x
=
5
3x
+
2y
=
7
2
+
y
=
3
+
x
a
+
b
=
b
+
a
(a、b已知)
5x
+
7
=
3x
-
5
3.
上面的式子的共同特点是什么?
都是等式。
我们可以用
a=
b
表示一般的等式
一、激发求知欲
未知数
等式
猜猜你的年龄
把你的年龄乘以2减去5的得数告诉我,我就能猜出你的年龄。
二、展示目标和任务
学习目标:
1.理解等式的两条性质;
2.会用等式的性质解简单的一元一次方程;
学习重难点:
1.理解和应用等式的性质;
2.应用等式的性质把简单的一元一次方程转化为x=a的形式。
等
式
a
=
b
+
+
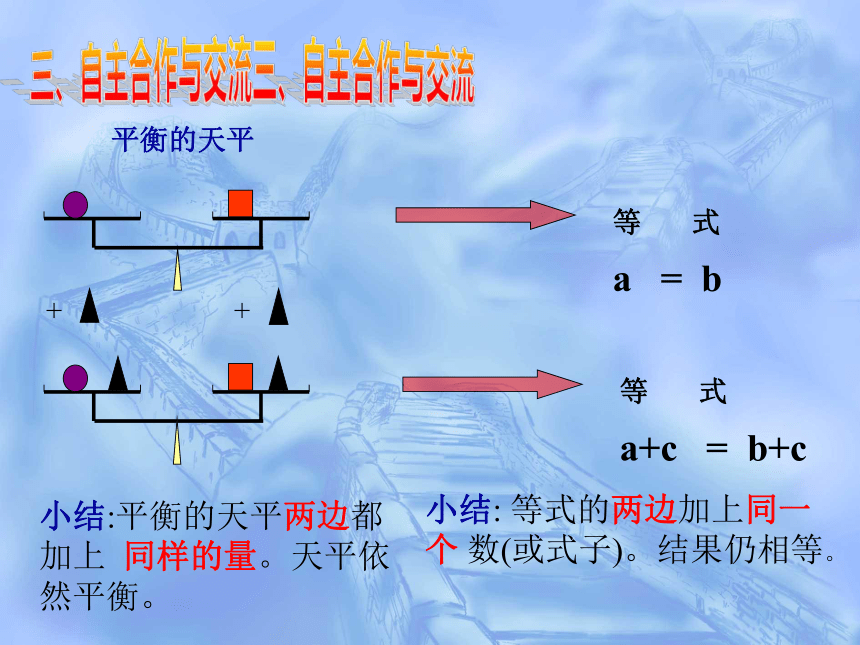
平衡的天平
小结:平衡的天平两边都加上
同样的量。天平依然平衡。
等
式
a+c
=
b+c
小结:
等式的两边加上同一个
数(或式子)。结果仍相等。
三、自主合作与交流
等
式
a
=
b
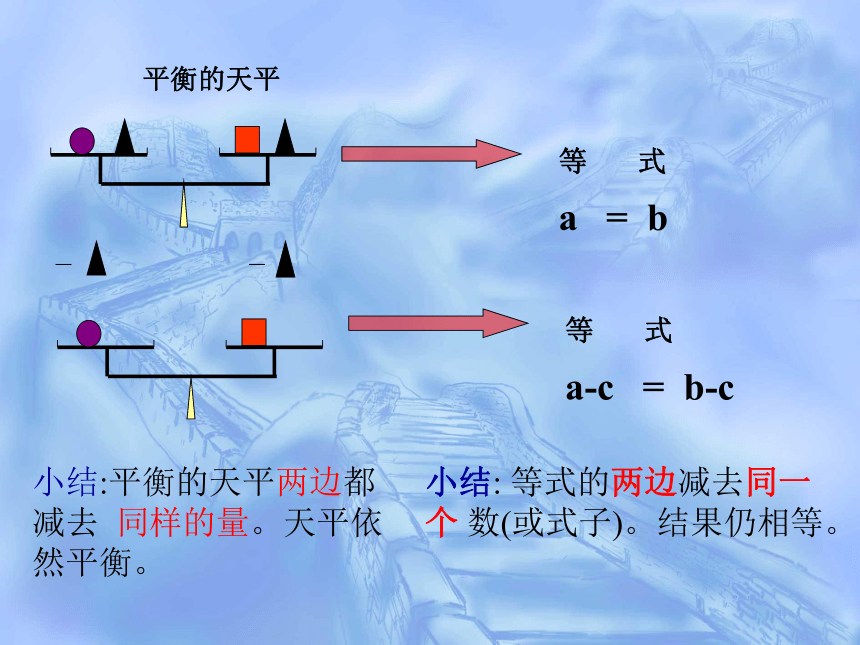
小结:平衡的天平两边都减去
同样的量。天平依然平衡。
小结:
等式的两边减去同一个
数(或式子)。结果仍相等。
-
-
平衡的天平
等
式
a-c
=
b-c
等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式
如果 ,那么
c
b
c
a
±
=
±
b
a
=
关键:
同侧对比
注意符号
5
(-4)
1.
用适当的数或式子填空,使结果仍是等式。
若
4x
=
7x
–
5
则
4x
+
=
7x
(2)
若
3a
+
4
=
8
则
3a
=
8
+
.
要求:
1.观察等式变形前后
两边各有什么变化
2.应怎样变化可使等
式依然相等
小试牛刀
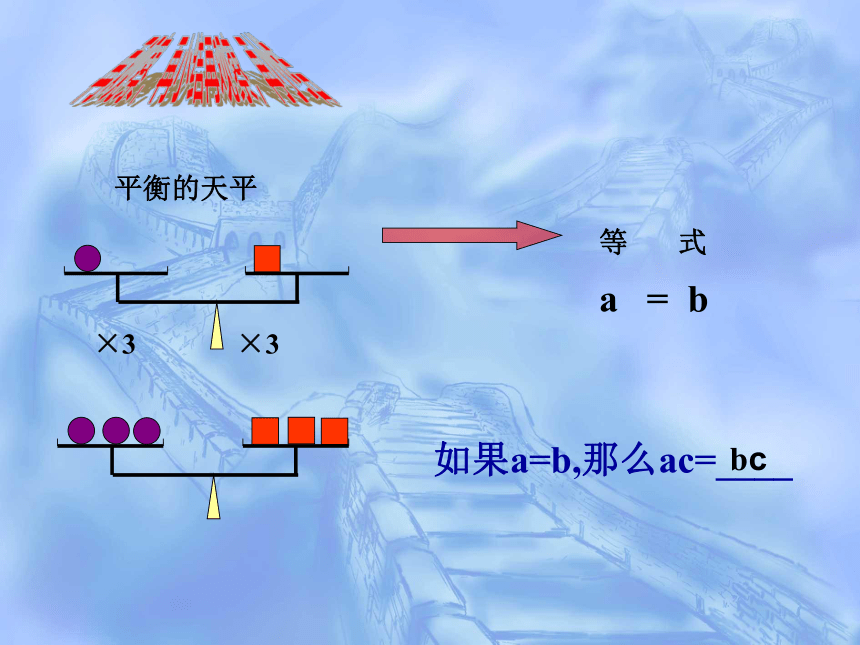
平衡的天平
×3
×3
等
式
a
=
b
如果a=b,那么ac=____
bc
再观察,再小结
÷3
÷3
如果
a
=
b
那么
a
b
c
c
__
__
=
(
c≠0)
等
式
a
=
b
平衡的天平
等式性质2
:等式两边同乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 ,那么
如果
,那么
b
a
=
bc
ac
=
b
a
=
(
)
0
?
c
c
b
c
a
=
(1)
3x
=
-
9
两边都____
得 x
=
-3
(3)
2x
+
1
=
3
两边都____
得 2x
=
______
两边都____
得 x
=
_______
(2)
-
0.5x
=
2
两边都___
得 x
=
_____
除以3
除以
-0.5
-
4
减去1
2
用适当的数或式子填空,使结果仍是等式。
关键:
同侧对比
注意符号
展现自我
除以2
1
四、成果展示,教师点拨
等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式
等式性质2
:等式两边同乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 ,那么
如果
,那么
b
a
=
bc
ac
=
b
a
=
(
)
0
?
c
c
b
c
a
=
如果 ,那么
c
b
c
a
±
=
±
b
a
=
例1:解方程:
x+7=26
x=?
两边同减7
分析:
要使方程x+7=26转化为x=a(常数)的形式,要去掉方程左边的7.
解:两边都减7,得
x+7-7=26-
7
于是
x=19
例2:利用等式性质解下列方程
(1)
-5X=20
(2)
解:
(1)
两边同除以
-5,得
4
5
3
1
=
-
-
X
5
20
5
5
-
=
-
-
x
于是
x=-4
(2)两边同加5,得
4
5
3
1
=
+
-
X
化简,得
3
1
-
=
9
两边同除以
,
得
3
1
-
X
X=-27
1.填一填:
(1)如果3x+4=7,那么3x=________,其依据是________
,在等式的两边都________.
(2)如果-
2x=8,那么x=________,依据是________
,在等式的两边都________.
(3)如果-x=3,那么x=________
(4)
如果-2x=4,
,那么x
=________。
(5)
如果2x-
,那么6x-1=________.
3
等式的性质1
-2
-3
-4
等式的性质2
除以-2
减去4
2
五、知识验证提升
2.填依据:在下列各题的括号内,填上使等式成立的依据.
(1)
得
(
)
(2)
得
(
)
(3)
得
(
)
(4)
得
(
)
(5)
得
(
)
(6)
得
(
)
(7)
得
(
)
等式性质2
等式性质1
等式性质2
等式性质1
等式性质2
等式性质1
等式性质2
3.算一算:运用等式的性质,把下列各式变形为x=m的形式.
(1)2x-1=3;
(2)
(x-1)=3;
(3)
;
(4)
(2x-1)=1;
(5)3(
x-1)=0;
(6)
=2.
x=2
x=7
x=-1
x=3/2
x=2
x=10/3
1:用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x
=
5
-
3x,那么2x
+(
)=
5
②、如果0.2x
=
10,
那么x
=(
)
解:①、2x
+(
3x
)=
5
根据等式性质
1,等式两边都加上
3x。
②、x
=
50
根据等式性质
2,等式两边都除以
0.2
或乘以
5。
挑战自我
2.
已知:X=Y
,
字母a可取任何值
(1)等式X-5=Y-5成立吗?为什么?
(2)等式X-(5-a)=Y-(5-a)一定成立吗?为什么?
(3)等式5X=5Y成立吗?为什么?
(4)等式X(5-a)=Y(5-a)一定成立吗?为什么?
(5)等式-
=-
成立吗?为什么?
(6)等式——
=——
一定成立吗?为什么?
X
5
Y
5
X
5-a
Y
5-a
(成立)
(成立)
(以上两题等式性质1)
(成立)
(成立)
(成立)
(3、4、5题等式性质2)
(不一定成立)
当a=5时等式两边都没有意义
挑战自我
等式的性质
1:
等式两边加(或减)同一个数
(或式子),结果仍相等。
如果
a
=
b
那么
a
+
c
=
b
+
c
2:
等式两边乘同一个数或
除以
同一个不为0的数,结果仍相等。
如果
a
=
b
那么
ac
=
bc
如果
a
=
b
那么
a
b
c
c
__
__
=
(c≠0)
掌握关键:<1>
“两
边”
“同一个数(或式子)
”
<2>
“除以同一个不为0的数”
解方程的目标:
变形
x
=
a
(常数)
检验的方法
(代
入)
原方程
小结
1、关于x的方程
3x
–
10
=
mx
的解为2,那么你知道m的值是多少吗,为什么?
拓展能力
3.1.2
等式的性质
等
式
性
质
什么是方程?
方程是含有
______的____。
2.
指出下列式子中哪些是方程,哪些不是,并说明为什么?
3
+
x
=
5
3x
+
2y
=
7
2
+
y
=
3
+
x
a
+
b
=
b
+
a
(a、b已知)
5x
+
7
=
3x
-
5
3.
上面的式子的共同特点是什么?
都是等式。
我们可以用
a=
b
表示一般的等式
一、激发求知欲
未知数
等式
猜猜你的年龄
把你的年龄乘以2减去5的得数告诉我,我就能猜出你的年龄。
二、展示目标和任务
学习目标:
1.理解等式的两条性质;
2.会用等式的性质解简单的一元一次方程;
学习重难点:
1.理解和应用等式的性质;
2.应用等式的性质把简单的一元一次方程转化为x=a的形式。
等
式
a
=
b
+
+
平衡的天平
小结:平衡的天平两边都加上
同样的量。天平依然平衡。
等
式
a+c
=
b+c
小结:
等式的两边加上同一个
数(或式子)。结果仍相等。
三、自主合作与交流
等
式
a
=
b
小结:平衡的天平两边都减去
同样的量。天平依然平衡。
小结:
等式的两边减去同一个
数(或式子)。结果仍相等。
-
-
平衡的天平
等
式
a-c
=
b-c
等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式
如果 ,那么
c
b
c
a
±
=
±
b
a
=
关键:
同侧对比
注意符号
5
(-4)
1.
用适当的数或式子填空,使结果仍是等式。
若
4x
=
7x
–
5
则
4x
+
=
7x
(2)
若
3a
+
4
=
8
则
3a
=
8
+
.
要求:
1.观察等式变形前后
两边各有什么变化
2.应怎样变化可使等
式依然相等
小试牛刀
平衡的天平
×3
×3
等
式
a
=
b
如果a=b,那么ac=____
bc
再观察,再小结
÷3
÷3
如果
a
=
b
那么
a
b
c
c
__
__
=
(
c≠0)
等
式
a
=
b
平衡的天平
等式性质2
:等式两边同乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 ,那么
如果
,那么
b
a
=
bc
ac
=
b
a
=
(
)
0
?
c
c
b
c
a
=
(1)
3x
=
-
9
两边都____
得 x
=
-3
(3)
2x
+
1
=
3
两边都____
得 2x
=
______
两边都____
得 x
=
_______
(2)
-
0.5x
=
2
两边都___
得 x
=
_____
除以3
除以
-0.5
-
4
减去1
2
用适当的数或式子填空,使结果仍是等式。
关键:
同侧对比
注意符号
展现自我
除以2
1
四、成果展示,教师点拨
等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式
等式性质2
:等式两边同乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 ,那么
如果
,那么
b
a
=
bc
ac
=
b
a
=
(
)
0
?
c
c
b
c
a
=
如果 ,那么
c
b
c
a
±
=
±
b
a
=
例1:解方程:
x+7=26
x=?
两边同减7
分析:
要使方程x+7=26转化为x=a(常数)的形式,要去掉方程左边的7.
解:两边都减7,得
x+7-7=26-
7
于是
x=19
例2:利用等式性质解下列方程
(1)
-5X=20
(2)
解:
(1)
两边同除以
-5,得
4
5
3
1
=
-
-
X
5
20
5
5
-
=
-
-
x
于是
x=-4
(2)两边同加5,得
4
5
3
1
=
+
-
X
化简,得
3
1
-
=
9
两边同除以
,
得
3
1
-
X
X=-27
1.填一填:
(1)如果3x+4=7,那么3x=________,其依据是________
,在等式的两边都________.
(2)如果-
2x=8,那么x=________,依据是________
,在等式的两边都________.
(3)如果-x=3,那么x=________
(4)
如果-2x=4,
,那么x
=________。
(5)
如果2x-
,那么6x-1=________.
3
等式的性质1
-2
-3
-4
等式的性质2
除以-2
减去4
2
五、知识验证提升
2.填依据:在下列各题的括号内,填上使等式成立的依据.
(1)
得
(
)
(2)
得
(
)
(3)
得
(
)
(4)
得
(
)
(5)
得
(
)
(6)
得
(
)
(7)
得
(
)
等式性质2
等式性质1
等式性质2
等式性质1
等式性质2
等式性质1
等式性质2
3.算一算:运用等式的性质,把下列各式变形为x=m的形式.
(1)2x-1=3;
(2)
(x-1)=3;
(3)
;
(4)
(2x-1)=1;
(5)3(
x-1)=0;
(6)
=2.
x=2
x=7
x=-1
x=3/2
x=2
x=10/3
1:用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x
=
5
-
3x,那么2x
+(
)=
5
②、如果0.2x
=
10,
那么x
=(
)
解:①、2x
+(
3x
)=
5
根据等式性质
1,等式两边都加上
3x。
②、x
=
50
根据等式性质
2,等式两边都除以
0.2
或乘以
5。
挑战自我
2.
已知:X=Y
,
字母a可取任何值
(1)等式X-5=Y-5成立吗?为什么?
(2)等式X-(5-a)=Y-(5-a)一定成立吗?为什么?
(3)等式5X=5Y成立吗?为什么?
(4)等式X(5-a)=Y(5-a)一定成立吗?为什么?
(5)等式-
=-
成立吗?为什么?
(6)等式——
=——
一定成立吗?为什么?
X
5
Y
5
X
5-a
Y
5-a
(成立)
(成立)
(以上两题等式性质1)
(成立)
(成立)
(成立)
(3、4、5题等式性质2)
(不一定成立)
当a=5时等式两边都没有意义
挑战自我
等式的性质
1:
等式两边加(或减)同一个数
(或式子),结果仍相等。
如果
a
=
b
那么
a
+
c
=
b
+
c
2:
等式两边乘同一个数或
除以
同一个不为0的数,结果仍相等。
如果
a
=
b
那么
ac
=
bc
如果
a
=
b
那么
a
b
c
c
__
__
=
(c≠0)
掌握关键:<1>
“两
边”
“同一个数(或式子)
”
<2>
“除以同一个不为0的数”
解方程的目标:
变形
x
=
a
(常数)
检验的方法
(代
入)
原方程
小结
1、关于x的方程
3x
–
10
=
mx
的解为2,那么你知道m的值是多少吗,为什么?
拓展能力
