2020年秋华东师大版 数学七年级上册4.2.1 由立体图形到视图课件(共32张PPT)
文档属性
| 名称 | 2020年秋华东师大版 数学七年级上册4.2.1 由立体图形到视图课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:27:42 | ||
图片预览







文档简介
(共32张PPT)
第4章
图形的初步认识
4.2
立体图形的视图
4.2.1
由立体图形到视图
华师版数学七年级上册
1.让学生了解三视图与现实生活的联系,会画简单的三视图;
2.通过从不同的方向关察物体,培养学生的空间观念;
3.通过观察思考,得到视图的不同效果,培养学生主动参与意识,激发学习兴趣.
学习目标
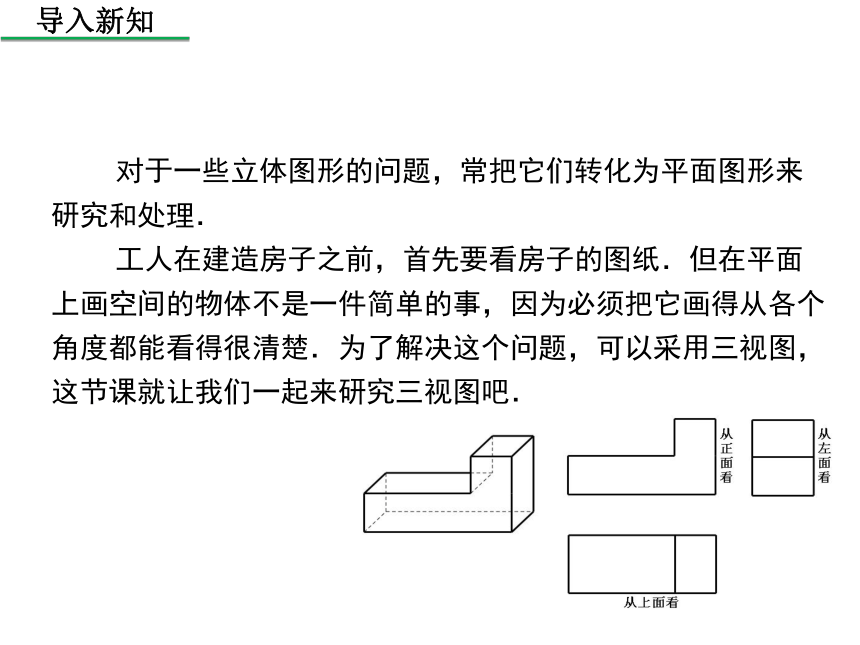
对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.
工人在建造房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.为了解决这个问题,可以采用三视图,这节课就让我们一起来研究三视图吧.
导入新知
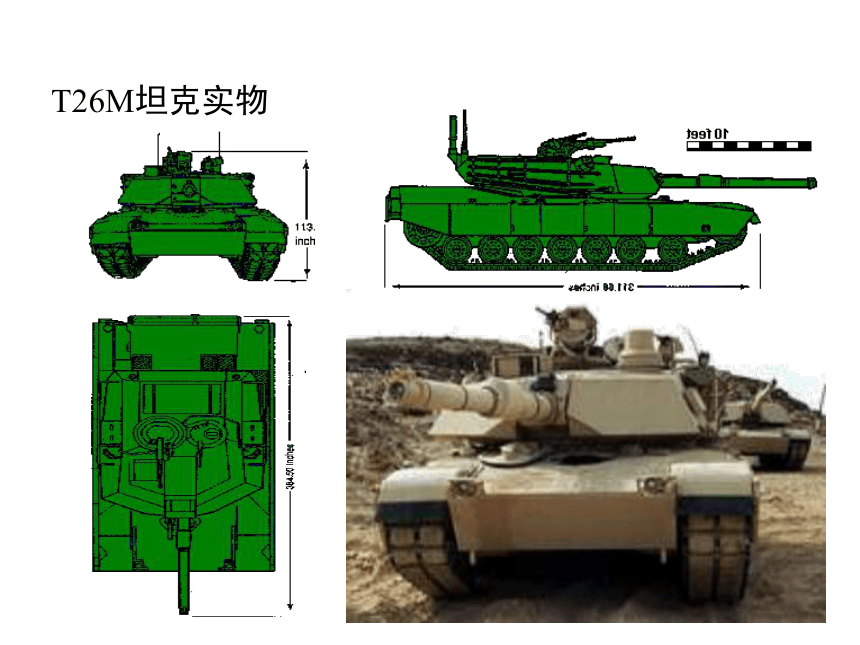
T26M坦克实物
摩托车
知识模块一 中心投影和平行投影
阅读教材P123~P126,完成下面的内容.
归纳:视图来自于投影,而投影又分为中心投影和平行投影.
(1)________形成的投影称为中心投影;
(2)_________形成的投影称为平行投影.
点光源
平行光线
探究新知
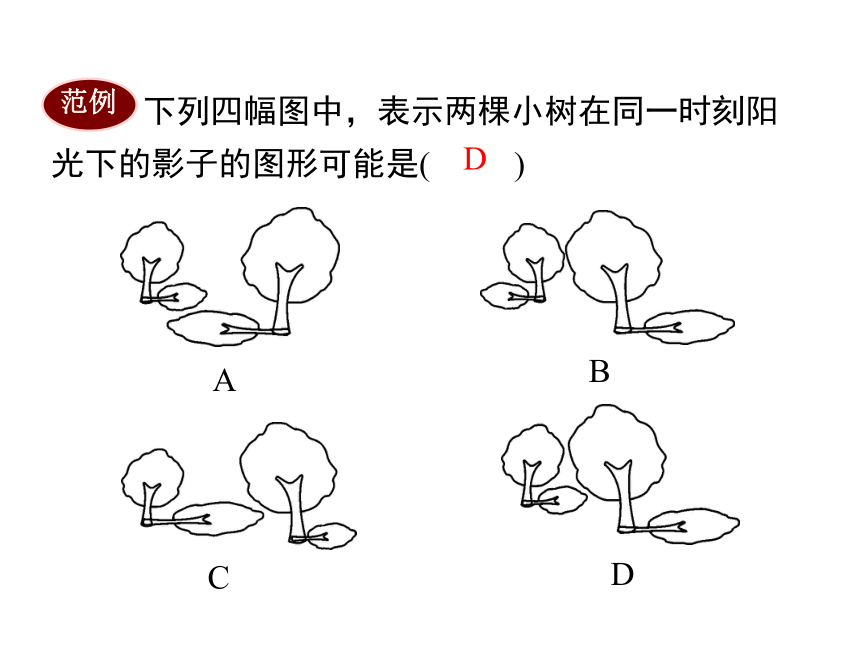
下列四幅图中,表示两棵小树在同一时刻阳光下的影子的图形可能是(
)
范例
A
B
C
D
D
仿例
下列投影中不属于中心投影的是(
)
A.晚上路灯下小孩的影子
B.汽车灯光照射下行人的影子
C.阳光下沙滩上人的影子
D.舞台上一束灯光下演员的影子
C
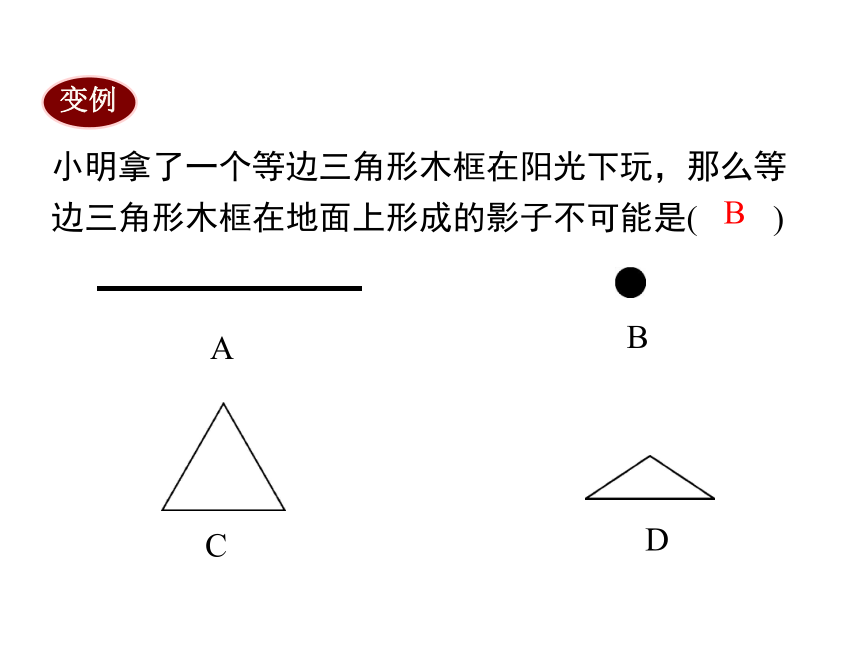
变例
小明拿了一个等边三角形木框在阳光下玩,那么等边三角形木框在地面上形成的影子不可能是(
)
A
B
C
D
B
知识模块二 由立体图形到视图
视图是一种特殊的平行投影.
从正面、上面和侧面(左面或右面)三个不同的方向进行平行投影,可以得到三个投影,这样就可以用平面图形去刻画一个立体图形了.
归纳
从正面得到的投影,称为______;从上面得到的投影,称为_______;从侧面得到的投影,称为______.依投影方向不同,有左视图和右视图.通常将_______、________、与__________称为一个物体的三视图.
主视图
俯视图
侧视图
主视图
俯视图
左(右)视图
从正面得到的投影
从上面得到的投影
从侧面得到的投影,
立体图形的三视图:主视图、俯视图、侧视图
主视图:
俯视图:
侧视图:
分左视图和右视图
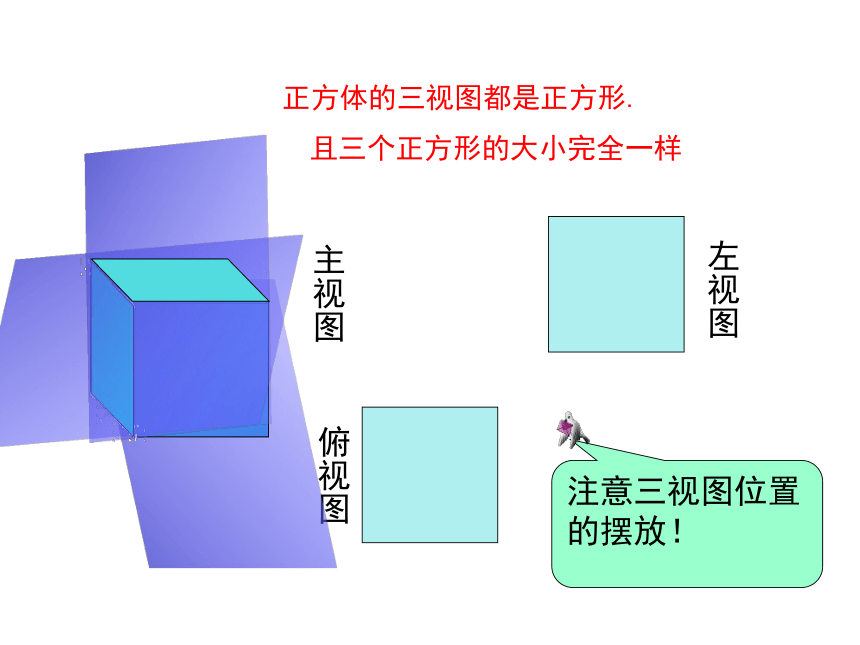
主视图
正方体的三视图都是正方形.
俯视图
左视图
注意三视图位置的摆放!
且三个正方形的大小完全一样
圆柱的主视图和左视图都是长方形,两个长方形大小完全一样,俯视图是圆。
主视图
左视图
俯视图
注意三视图位置的摆放!
若是一个横放的圆柱,三视图又该怎样呢?
横放圆柱的三视图:
主视图
俯视图
左视图
若是一个平放的圆柱,三视图又该怎样呢?
平放圆柱的三视图:
主视图
俯视图
左视图
那么圆锥的三视图又该怎样呢?
主视图
俯视图
左视图
圆锥的主视图和左视图都是三角形,两个三
角形的大小完全一样。俯视图为带圆心的圆.
若是一个倒放的圆锥,三视图又该怎样呢?
倒圆锥的三视图.
主视图
左视图
俯
视
图
那么三棱锥的三视图又该怎样呢?
正三棱锥的三视图:
主视图
俯视图
左视图
注意:画三视图时看得见的线都要画上去.
正四棱锥的三视图:
正视图
俯视图
左视图
注意:棱锥俯视图正方形两对角线不能漏!
那么球体的三视图又该怎样呢?
主视图
俯视图
左视图
球体的三视图:
球体的三视图为三个大小完全一样的圆
范例
画出如下图所示的一些基本几何体的三视图.
解:如图.
仿例
如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图不变,左视图不变
D.主视图改变,左视图不变
D
仿例
如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图不变,左视图不变
D.主视图改变,左视图不变
D
变例
如图是由几个小正方体搭成的几何体的俯视图,小正方形中的数字表示在该处的小正方体的个数,请画出这几个几何体的主视图和左视图.
解:如下图所示:
课堂练习
1.如图乙的几何体,其三视图分别是图甲中三个图形的是(
)
主视图
俯视图
左视图
甲
A
B
C
D
乙
A
2.如图所示是由相同小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的左视图是(
)
A
B
C
D
B
3.一个物体的三视图如图所示,该立体图形是
.
主视图
左视图
俯视图
圆台
4.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是
.
主视图
俯视图
4或5
5.如图是用若干个大小相同的正方体搭成的一个立体图形的三视图.
根据三视图回答:该立体图形由多少个小正方体构成?
主视图
左视图
俯视图
解:5个.
6.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图所示.
主视图
俯视图
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
解:(1)左视图有以下5种情形:
(2)n=8,9,10,11.
再见
第4章
图形的初步认识
4.2
立体图形的视图
4.2.1
由立体图形到视图
华师版数学七年级上册
1.让学生了解三视图与现实生活的联系,会画简单的三视图;
2.通过从不同的方向关察物体,培养学生的空间观念;
3.通过观察思考,得到视图的不同效果,培养学生主动参与意识,激发学习兴趣.
学习目标
对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.
工人在建造房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.为了解决这个问题,可以采用三视图,这节课就让我们一起来研究三视图吧.
导入新知
T26M坦克实物
摩托车
知识模块一 中心投影和平行投影
阅读教材P123~P126,完成下面的内容.
归纳:视图来自于投影,而投影又分为中心投影和平行投影.
(1)________形成的投影称为中心投影;
(2)_________形成的投影称为平行投影.
点光源
平行光线
探究新知
下列四幅图中,表示两棵小树在同一时刻阳光下的影子的图形可能是(
)
范例
A
B
C
D
D
仿例
下列投影中不属于中心投影的是(
)
A.晚上路灯下小孩的影子
B.汽车灯光照射下行人的影子
C.阳光下沙滩上人的影子
D.舞台上一束灯光下演员的影子
C
变例
小明拿了一个等边三角形木框在阳光下玩,那么等边三角形木框在地面上形成的影子不可能是(
)
A
B
C
D
B
知识模块二 由立体图形到视图
视图是一种特殊的平行投影.
从正面、上面和侧面(左面或右面)三个不同的方向进行平行投影,可以得到三个投影,这样就可以用平面图形去刻画一个立体图形了.
归纳
从正面得到的投影,称为______;从上面得到的投影,称为_______;从侧面得到的投影,称为______.依投影方向不同,有左视图和右视图.通常将_______、________、与__________称为一个物体的三视图.
主视图
俯视图
侧视图
主视图
俯视图
左(右)视图
从正面得到的投影
从上面得到的投影
从侧面得到的投影,
立体图形的三视图:主视图、俯视图、侧视图
主视图:
俯视图:
侧视图:
分左视图和右视图
主视图
正方体的三视图都是正方形.
俯视图
左视图
注意三视图位置的摆放!
且三个正方形的大小完全一样
圆柱的主视图和左视图都是长方形,两个长方形大小完全一样,俯视图是圆。
主视图
左视图
俯视图
注意三视图位置的摆放!
若是一个横放的圆柱,三视图又该怎样呢?
横放圆柱的三视图:
主视图
俯视图
左视图
若是一个平放的圆柱,三视图又该怎样呢?
平放圆柱的三视图:
主视图
俯视图
左视图
那么圆锥的三视图又该怎样呢?
主视图
俯视图
左视图
圆锥的主视图和左视图都是三角形,两个三
角形的大小完全一样。俯视图为带圆心的圆.
若是一个倒放的圆锥,三视图又该怎样呢?
倒圆锥的三视图.
主视图
左视图
俯
视
图
那么三棱锥的三视图又该怎样呢?
正三棱锥的三视图:
主视图
俯视图
左视图
注意:画三视图时看得见的线都要画上去.
正四棱锥的三视图:
正视图
俯视图
左视图
注意:棱锥俯视图正方形两对角线不能漏!
那么球体的三视图又该怎样呢?
主视图
俯视图
左视图
球体的三视图:
球体的三视图为三个大小完全一样的圆
范例
画出如下图所示的一些基本几何体的三视图.
解:如图.
仿例
如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图不变,左视图不变
D.主视图改变,左视图不变
D
仿例
如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图不变,左视图不变
D.主视图改变,左视图不变
D
变例
如图是由几个小正方体搭成的几何体的俯视图,小正方形中的数字表示在该处的小正方体的个数,请画出这几个几何体的主视图和左视图.
解:如下图所示:
课堂练习
1.如图乙的几何体,其三视图分别是图甲中三个图形的是(
)
主视图
俯视图
左视图
甲
A
B
C
D
乙
A
2.如图所示是由相同小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的左视图是(
)
A
B
C
D
B
3.一个物体的三视图如图所示,该立体图形是
.
主视图
左视图
俯视图
圆台
4.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是
.
主视图
俯视图
4或5
5.如图是用若干个大小相同的正方体搭成的一个立体图形的三视图.
根据三视图回答:该立体图形由多少个小正方体构成?
主视图
左视图
俯视图
解:5个.
6.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图所示.
主视图
俯视图
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
解:(1)左视图有以下5种情形:
(2)n=8,9,10,11.
再见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
