二次函数y=ax2+bx+c的图象和性质教学课件
文档属性
| 名称 | 二次函数y=ax2+bx+c的图象和性质教学课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 865.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-15 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
二次函数 的图象(1)
2.4
x
y
课件制作与完善:济宁十二中 陈伟利
看黑板填下表,回答问题:
开口
方向 对称轴 顶点坐标
温故引新
二次函数 的图象可以由 的图象经过怎样的平移得到?
回顾:二次函数y= ax2+c的图象可以由 y=ax2 的图象
当c > 0 时 向上平移|c|个单位得到.
当c < 0 时 向下平移|c|个单位得到.
想一想: 的图象是怎样的?
x … -3 -2 -1 0 1 2 3 4 …
… 4.5 2 0.5 0 0.5 2 4.5 …
… …
自主合作1 函数y=a(x-h)2的图象和性质
(1)观察并补充下表,比较它们的值之间有什么关系?
(2)用铅笔在纸上作二次函数y= (x-1)2的图象.
探索新知
描点、连线
4.5
2
0.5
0
0.5
2
4.5
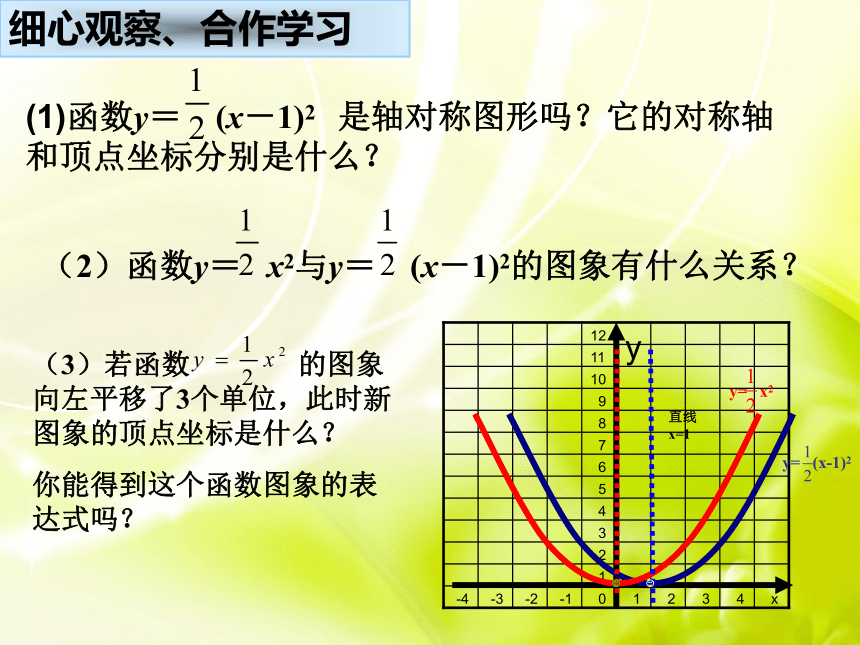
细心观察、合作学习
(1)函数y= (x-1)2 是轴对称图形吗?它的对称轴
和顶点坐标分别是什么?
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
y= (x-1)2
(2)函数y= x2与y= (x-1)2的图象有什么关系?
(3)若函数 的图象向左平移了3个单位,此时新图象的顶点坐标是什么?
你能得到这个函数图象的表达式吗?
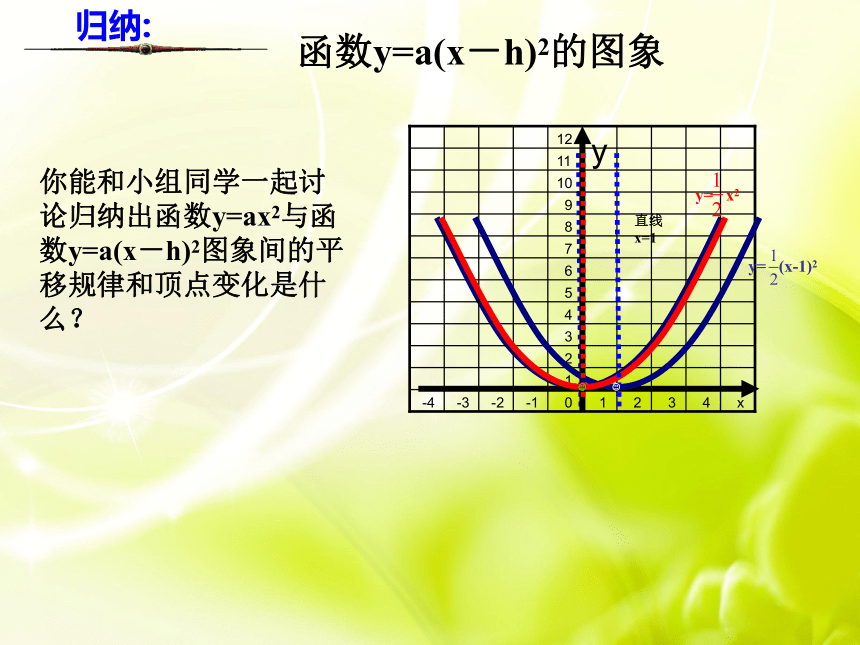
函数y=a(x-h)2的图象
归纳:
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
y= (x-1)2
你能和小组同学一起讨论归纳出函数y=ax2与函数y=a(x-h)2图象间的平移规律和顶点变化是什么?
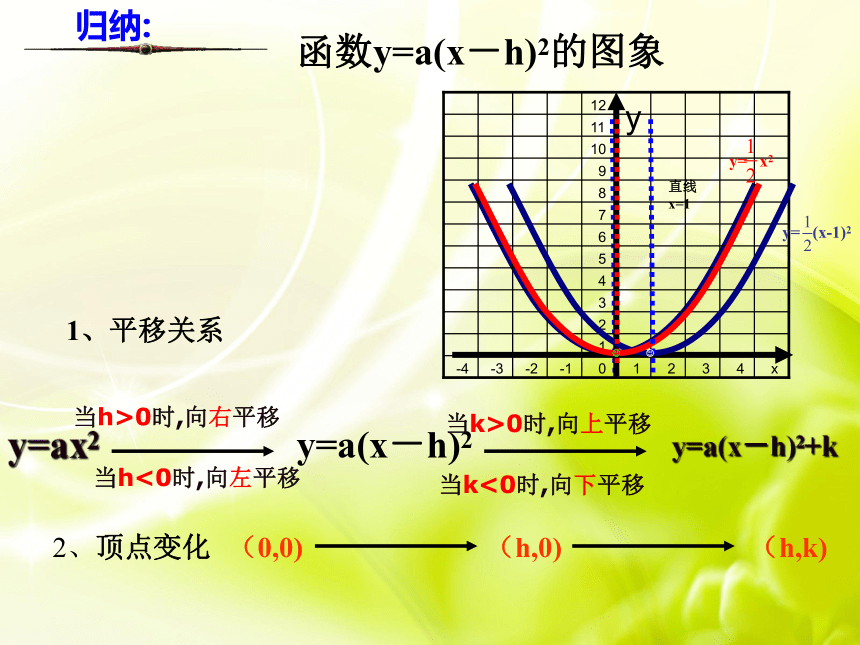
函数y=a(x-h)2的图象
1、平移关系
2、顶点变化
当h>0时,向右平移
当h<0时,向左平移
y=ax2
y=a(x-h)2
(h,0)
归纳:
(0,0)
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
y= (x-1)2
(h,k)
当k>0时,向上平移
当k<0时,向下平移
y=a(x-h)2+k
不画图象填写下表
抛物线 开口方向 顶点坐标 对称轴
y =2(x+3)2
y = -3(x-1)2 +1
y=0.5(x+2)2-1
y = -4(x-3)2 +2
上
(-3,0)
直线x=-3
下
(1,1)
直线x=1
上
(-2,-1)
直线x=-2
下
(3,2)
直线x=3
函数的增减性
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
x=1
议一议:函数
的增减性是怎样的?
呢?
呢?
关键:找到函数的对称轴
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
找一找这3个函数图象间有什么关系?
函数y=a(x-h)2+k的图象和性质
所以二次函数y= x2 , ,
的图象都是抛物线,并且形状相同,只是位置不同,将函数
的图象向右平移一个单位,就得到函数
的图象;再向上平移2个单位,就得到函数
的图象.
一般地,平移二次函数y=ax2的图象就可得到二次函数y=a(x-h)2+k的图象。因此,二次函数y=a(x -h)2+k它的形状、对称轴、顶点坐标和开口方向与a、h、k的值有关。
y= a(x-h)2+k 开口
方向 对称轴 顶点坐标
a > 0
a < 0
向上 直线x=h (h,k)
向下 直线x=h (h,k)
1.二次函数y=3(x+1)2+4的图象可由二次函数y=3x2如何平移形成,它的对称轴和顶点坐标分别是什么?
2.把函数的y=-3(x-4)2-2图象作怎样的平移变换,就能得到函数y=-3x2的图象。
先向左平移4个单位,再向上平移2个单位
3.如果一条抛物线的形状与y=3x2+2的形状相同,且顶点坐标是(4,-2),则函数关系式是 。
大家一起移一移
已知二次函数 的图象,移一移后看看是什么函数了?
大家一起移一移
已知二次函数 的图象,移一移后看看是什么函数了?
1、平移关系
2、顶点变化
当h>0时,向右平移
当h<0时,向左平移
y=ax2
y=a(x-h)2
(h,0)
(0,0)
当k>0时,向上平移
当k<0时,向下平移
y=a(x-h)2+k
(h,k)
小结 收获
二次函数y=a(x-h) +k与y=ax 的关系
课后拓展
1、二次函数y=0.5(x+2)2-1与y=0.5(x-1)2+2的图象是由函数y=0.5x2的图象怎样移动得到的?
它们之间是通过怎样移动得到的?
二次函数 的图象(1)
2.4
x
y
课件制作与完善:济宁十二中 陈伟利
看黑板填下表,回答问题:
开口
方向 对称轴 顶点坐标
温故引新
二次函数 的图象可以由 的图象经过怎样的平移得到?
回顾:二次函数y= ax2+c的图象可以由 y=ax2 的图象
当c > 0 时 向上平移|c|个单位得到.
当c < 0 时 向下平移|c|个单位得到.
想一想: 的图象是怎样的?
x … -3 -2 -1 0 1 2 3 4 …
… 4.5 2 0.5 0 0.5 2 4.5 …
… …
自主合作1 函数y=a(x-h)2的图象和性质
(1)观察并补充下表,比较它们的值之间有什么关系?
(2)用铅笔在纸上作二次函数y= (x-1)2的图象.
探索新知
描点、连线
4.5
2
0.5
0
0.5
2
4.5
细心观察、合作学习
(1)函数y= (x-1)2 是轴对称图形吗?它的对称轴
和顶点坐标分别是什么?
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
y= (x-1)2
(2)函数y= x2与y= (x-1)2的图象有什么关系?
(3)若函数 的图象向左平移了3个单位,此时新图象的顶点坐标是什么?
你能得到这个函数图象的表达式吗?
函数y=a(x-h)2的图象
归纳:
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
y= (x-1)2
你能和小组同学一起讨论归纳出函数y=ax2与函数y=a(x-h)2图象间的平移规律和顶点变化是什么?
函数y=a(x-h)2的图象
1、平移关系
2、顶点变化
当h>0时,向右平移
当h<0时,向左平移
y=ax2
y=a(x-h)2
(h,0)
归纳:
(0,0)
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
y= (x-1)2
(h,k)
当k>0时,向上平移
当k<0时,向下平移
y=a(x-h)2+k
不画图象填写下表
抛物线 开口方向 顶点坐标 对称轴
y =2(x+3)2
y = -3(x-1)2 +1
y=0.5(x+2)2-1
y = -4(x-3)2 +2
上
(-3,0)
直线x=-3
下
(1,1)
直线x=1
上
(-2,-1)
直线x=-2
下
(3,2)
直线x=3
函数的增减性
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
x=1
议一议:函数
的增减性是怎样的?
呢?
呢?
关键:找到函数的对称轴
1
11
y
12
x
4
3
2
1
0
-1
-2
-3
-4
2
3
4
5
6
7
8
9
10
y= x2
直线x=1
找一找这3个函数图象间有什么关系?
函数y=a(x-h)2+k的图象和性质
所以二次函数y= x2 , ,
的图象都是抛物线,并且形状相同,只是位置不同,将函数
的图象向右平移一个单位,就得到函数
的图象;再向上平移2个单位,就得到函数
的图象.
一般地,平移二次函数y=ax2的图象就可得到二次函数y=a(x-h)2+k的图象。因此,二次函数y=a(x -h)2+k它的形状、对称轴、顶点坐标和开口方向与a、h、k的值有关。
y= a(x-h)2+k 开口
方向 对称轴 顶点坐标
a > 0
a < 0
向上 直线x=h (h,k)
向下 直线x=h (h,k)
1.二次函数y=3(x+1)2+4的图象可由二次函数y=3x2如何平移形成,它的对称轴和顶点坐标分别是什么?
2.把函数的y=-3(x-4)2-2图象作怎样的平移变换,就能得到函数y=-3x2的图象。
先向左平移4个单位,再向上平移2个单位
3.如果一条抛物线的形状与y=3x2+2的形状相同,且顶点坐标是(4,-2),则函数关系式是 。
大家一起移一移
已知二次函数 的图象,移一移后看看是什么函数了?
大家一起移一移
已知二次函数 的图象,移一移后看看是什么函数了?
1、平移关系
2、顶点变化
当h>0时,向右平移
当h<0时,向左平移
y=ax2
y=a(x-h)2
(h,0)
(0,0)
当k>0时,向上平移
当k<0时,向下平移
y=a(x-h)2+k
(h,k)
小结 收获
二次函数y=a(x-h) +k与y=ax 的关系
课后拓展
1、二次函数y=0.5(x+2)2-1与y=0.5(x-1)2+2的图象是由函数y=0.5x2的图象怎样移动得到的?
它们之间是通过怎样移动得到的?
