人教版九年级数学上册21.3实际问题与一元二次方程课件(所有分类 36张)
文档属性
| 名称 | 人教版九年级数学上册21.3实际问题与一元二次方程课件(所有分类 36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 312.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 17:29:15 | ||
图片预览











文档简介
(共36张PPT)
一、传播问题:
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,求每轮感染中平均一台电脑能感染几台?若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过700台?
某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型H1N1流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
二、增长率问题:
课前热身1:二中小明学习非常认真,学习成绩直线上升,
第一次月考数学成绩是a分,第二次月考增长了10%,
第三次月考又增长了10%,问他第三次数学成绩是多少?
分析:
第三次
第二次
第一次
a
aX10%
a+aX10%=
a(1+10%)X10%
a(1+10%)+
a(1+10%)
X10%
=
a(1+10%)2
a(1+10%)
例1:平阳按“九五”国民经济发展规划要求,2003年的社会总产值要比2001年增长21%,求平均每年增长的百分率.(提示:基数为2001年的社会总产值,可视为a)
设每年增长率为x,2001年的总产值为a,则
2001年
a
2002年
a(1+x)
2003年
a(1+x)
2
增长21%
a
a+21%a
a(1+x)
2
=a+21%a
分析:
a
(1+x)
2
=1.21
a
(1+x)
2
=1.21
1+x
=1.1
x
=0.1
解:设每年增长率为x,2001年的总产值为a,则
a(1+x)
2
=a+21%a
答:平均每年增长的百分率为10%
.
练习1:某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,
每次降价的百分率为
x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
练习2:某药品两次升价,零售价升为原来的
1.2倍,已知两次升价的百分率一样,求每次升价的百分率(精确到0.1%)
解,设原价为
元,每次升价的百分率为
,
根据题意,得
解这个方程,得
由于升价的百分率不可能是负数,
所以
不合题意,舍去
答:每次升价的百分率为9.5%.
?练习4.市第四中学初三年级初一开学时就参加课程改革试验,重视学生能力培养.初一阶段就有48人在市级以上各项活动中得奖,之后逐年增加,到三年级结束共有183人次在市级以上得奖.求这两年中得奖人次的平均年增长率.
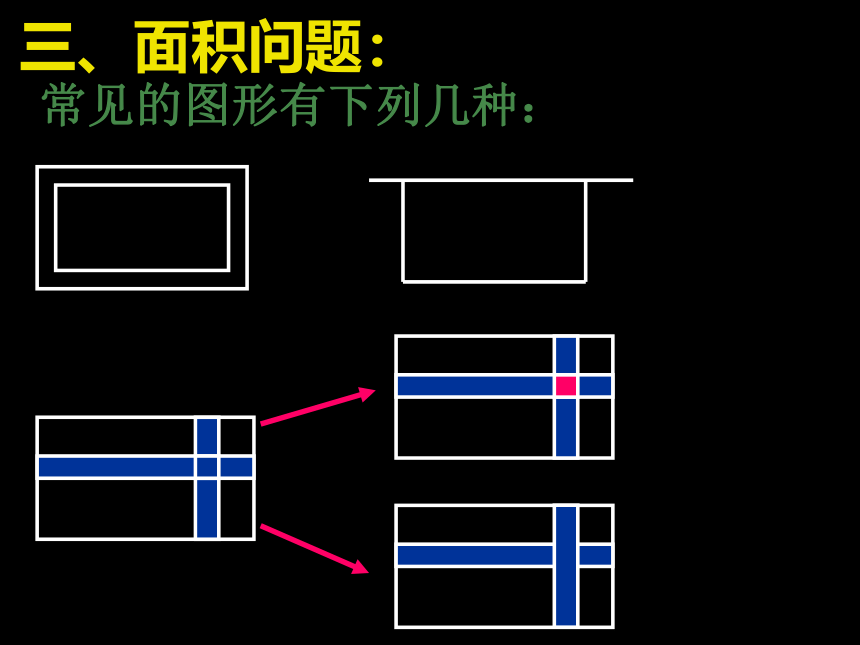
三、面积问题:
常见的图形有下列几种:
例1、用22cm长的铁丝,折成一个面积为30cm2的矩形。求这个矩形的长与宽.
整理后,得x2-11x+30=0
解这个方程,得x1=5,x2=6
(与题设不符,舍去)
答:这个矩形的长是6cm,宽是5cm。
由x1=5得
由x2=6,得
解:设这个矩形的长为xcm,则宽为
(cm).
根据题意,得
例2、在宽为20米、长为32米的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为耕地,要使耕地面积为540米2,道路的宽应为多少?
32m
20m
则横向的路面面积为
,
32m
20m
x米
分析:此题的相等关系是矩形面积减去道路面积等于540米2。
解法一、
如图,设道路的宽为x米,
32x
米2
纵向的路面面积为
。
20x
米2
注意:这两个面积的重叠部分是
x2
米2
所列的方程是不是
?
图中的道路面积不是
米2,
解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)
横向路面为
,
32m
20m
xm
xm
如图,设路宽为x米,
32x
米2
纵向路面面积为
。
20x
米2
耕地矩形的长(横向)为
,
耕地矩形的宽(纵向)为
。
相等关系是:耕地长×耕地宽=540米2
(20-x)
米
(32-x)
米
即
化简得:
再往下的计算、格式书写与解法1相同。
练习1:用一根长22厘米的铁丝,能否折成一个面积是30厘米的矩形?能否折成一个面积为32厘米的矩形?说明理由。
2:在一块长80米,宽60米的运动场外围修筑了一条宽度相等的跑道,这条跑道的面积是1500平方米,求这条跑道的宽度。
3.
如图,在长为40米,宽为22米的矩形地面上,修筑两条同样宽的互相垂直的道路,余下的铺上草坪,要使草坪的面积为760平方米,道路的宽应为多少?
40米
22米
4、如图,在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路,(两条纵向,一条横向,横向与纵向相互垂直),把耕地分成大小相等的六块试验地,要使试验地面积为570m?,问道路的宽为多少?
例3、求截去的正方形的边长
用一块长28cm、宽
20cm的长方形纸片,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体盒子,使它的底面积为180cm2,为了有效地利用材料,求截去的小正方形的边长是多少cm?
求截去的正方形的边长
分析
设截去的正方形的边长为xcm之后,关键在于列出底面(图中阴影部分)长和宽的代数式.结合图示和原有长方形的长和宽,不难得出这一代数式.
20-2x
28-2x
28cm
20cm
求截去的正方形边长
解:设截去的正方形的边长为xcm,根据题意,得
(28-2x)(20-2x)=180
x2-24x+95=0
解这个方程,得:x1=5,x2=19
经检验:x2=19不合题意,舍去.
所以截去的正方形边长为5cm.
例4:建造一个池底为正方形,深度为2.5m的长方体无盖蓄水池,建造池壁的单价是120元/m2,建造池底的单价是240元/m2,总造价是8640元,求池底的边长.
分析:池底的造价+池壁的造价=总造价
解:设池底的边长是xm.
根据题意得:
解方程得:
∵池底的边长不能为负数,∴取x=4
答:池底的边长是4m.
练习、建造成一个长方体形的水池,原计划水池深3米,水池周围为1400米,经过研讨,修改原方案,要把长与宽两边都增加原方案中的宽的2倍,于是新方案的水池容积为270万米3,求原来方案的水池的长与宽各是多少米?
700--x
x
3
700-x+2x
x+2x
x
原方案
新方案
课堂练习:列方程解下列应用题
1、学生会准备举办一次摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶嵌上一圈等宽的彩纸。经试验,彩纸面积为相片面积的2/3时较美观,求镶上彩纸条的宽。(精确到0.1厘米)
2、在宽20米,长32米的矩形地面上修筑同样宽的四条互相垂直的“井”字形道路(如图),余下的部分做绿地,要使绿地面积为448平方
米,路宽为多少?
32
20
3、小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子。如果要求长方体的底面面积为81平方厘米,那么剪去的正方形边长为多少?
4、学校课外生物(小组的试验园地是一块长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小路(如图),要使种植面积为600平方米,求小道的宽。(精确到0.1米)
5、
在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框。已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm2,求这个长方形框的框边宽。
X
X
30cm
20cm
解:设长方形框的边宽为xcm,依题意,得
30×20–(30–2x)(20–2x)=400
整理得
x2–
25+100=0
得
x1=20,
x2=5
当=20时,20-2x=
-20(舍去);当x=5时,20-2x=10
答:这个长方形框的框边宽为5cm
列一元二次方程解应题
6、放铅笔的V形槽如图,每往上一层可以多
放一支铅笔.现有190支铅笔,则要放几层
?
解:要放x层,则每一层放(1+x)
支铅笔.得
x
(1+x)
=190×2
X+
X
-380=0
解得X1=19,
X2=
-
20(不合题意)
答:要放19层.
2
列一元二次方程解应题
补充练习:
(98年北京市崇文区中考题)如图,有一面
积是150平方米的长方形鸡场,鸡场的一边靠墙
(墙长18米),墙对面有一个2米宽的门,另三边
(门除外)用竹篱笆围成,篱笆总长33米.求鸡
场的长和宽各多少米?
四、利润问题:总利润=单件利润
销量
1、爱家超市将进货单价为40元的商品,按50元销售时,能卖出500个,已知该商品每涨1元钱就少卖10个。为了赚8000元的利润,应涨多少元钱?
2、某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,经量减少库存,商场决定适当的降低售价,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件,若商场平均每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价多少元?
3、某商户以2元/千克的价格,购进一批小西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该商户决定降价出售,经调查发现,这种小西瓜每降价0.1元/千克,每天可多售出40千克,另外每天的房租等固定成本共24元,该商户要想每天盈利200元,应该将每千克的小西瓜的售价降低多少元?
五、球赛问题:(握手、签合同、打电话、送礼)
要组织一场篮球联赛,赛制为单循环形式(每两个队只赛一场)。计划安排15场比赛,应邀请多少个球队参加比赛?
参加一次聚会的每两个人都握了一次手,所有人共握手36次,有多少人参加聚会?
六、数字问题:
1.一个两位数,十位数字与个位数字之和为5,把这个数的十位数字与个位数字对调后,所得的新两位数与原两位数乘积为736,求原两位数。
2、有一个两位数,它的个位上的数字与十位上的数字之和是6,如果把它的个位数字与十位数字调换位置,所得的两位数乘以原来的两位数所得的积等于1008,求调换位置后得到的两位数。
一、传播问题:
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,求每轮感染中平均一台电脑能感染几台?若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过700台?
某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型H1N1流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
二、增长率问题:
课前热身1:二中小明学习非常认真,学习成绩直线上升,
第一次月考数学成绩是a分,第二次月考增长了10%,
第三次月考又增长了10%,问他第三次数学成绩是多少?
分析:
第三次
第二次
第一次
a
aX10%
a+aX10%=
a(1+10%)X10%
a(1+10%)+
a(1+10%)
X10%
=
a(1+10%)2
a(1+10%)
例1:平阳按“九五”国民经济发展规划要求,2003年的社会总产值要比2001年增长21%,求平均每年增长的百分率.(提示:基数为2001年的社会总产值,可视为a)
设每年增长率为x,2001年的总产值为a,则
2001年
a
2002年
a(1+x)
2003年
a(1+x)
2
增长21%
a
a+21%a
a(1+x)
2
=a+21%a
分析:
a
(1+x)
2
=1.21
a
(1+x)
2
=1.21
1+x
=1.1
x
=0.1
解:设每年增长率为x,2001年的总产值为a,则
a(1+x)
2
=a+21%a
答:平均每年增长的百分率为10%
.
练习1:某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,
每次降价的百分率为
x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
练习2:某药品两次升价,零售价升为原来的
1.2倍,已知两次升价的百分率一样,求每次升价的百分率(精确到0.1%)
解,设原价为
元,每次升价的百分率为
,
根据题意,得
解这个方程,得
由于升价的百分率不可能是负数,
所以
不合题意,舍去
答:每次升价的百分率为9.5%.
?练习4.市第四中学初三年级初一开学时就参加课程改革试验,重视学生能力培养.初一阶段就有48人在市级以上各项活动中得奖,之后逐年增加,到三年级结束共有183人次在市级以上得奖.求这两年中得奖人次的平均年增长率.
三、面积问题:
常见的图形有下列几种:
例1、用22cm长的铁丝,折成一个面积为30cm2的矩形。求这个矩形的长与宽.
整理后,得x2-11x+30=0
解这个方程,得x1=5,x2=6
(与题设不符,舍去)
答:这个矩形的长是6cm,宽是5cm。
由x1=5得
由x2=6,得
解:设这个矩形的长为xcm,则宽为
(cm).
根据题意,得
例2、在宽为20米、长为32米的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为耕地,要使耕地面积为540米2,道路的宽应为多少?
32m
20m
则横向的路面面积为
,
32m
20m
x米
分析:此题的相等关系是矩形面积减去道路面积等于540米2。
解法一、
如图,设道路的宽为x米,
32x
米2
纵向的路面面积为
。
20x
米2
注意:这两个面积的重叠部分是
x2
米2
所列的方程是不是
?
图中的道路面积不是
米2,
解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)
横向路面为
,
32m
20m
xm
xm
如图,设路宽为x米,
32x
米2
纵向路面面积为
。
20x
米2
耕地矩形的长(横向)为
,
耕地矩形的宽(纵向)为
。
相等关系是:耕地长×耕地宽=540米2
(20-x)
米
(32-x)
米
即
化简得:
再往下的计算、格式书写与解法1相同。
练习1:用一根长22厘米的铁丝,能否折成一个面积是30厘米的矩形?能否折成一个面积为32厘米的矩形?说明理由。
2:在一块长80米,宽60米的运动场外围修筑了一条宽度相等的跑道,这条跑道的面积是1500平方米,求这条跑道的宽度。
3.
如图,在长为40米,宽为22米的矩形地面上,修筑两条同样宽的互相垂直的道路,余下的铺上草坪,要使草坪的面积为760平方米,道路的宽应为多少?
40米
22米
4、如图,在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路,(两条纵向,一条横向,横向与纵向相互垂直),把耕地分成大小相等的六块试验地,要使试验地面积为570m?,问道路的宽为多少?
例3、求截去的正方形的边长
用一块长28cm、宽
20cm的长方形纸片,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体盒子,使它的底面积为180cm2,为了有效地利用材料,求截去的小正方形的边长是多少cm?
求截去的正方形的边长
分析
设截去的正方形的边长为xcm之后,关键在于列出底面(图中阴影部分)长和宽的代数式.结合图示和原有长方形的长和宽,不难得出这一代数式.
20-2x
28-2x
28cm
20cm
求截去的正方形边长
解:设截去的正方形的边长为xcm,根据题意,得
(28-2x)(20-2x)=180
x2-24x+95=0
解这个方程,得:x1=5,x2=19
经检验:x2=19不合题意,舍去.
所以截去的正方形边长为5cm.
例4:建造一个池底为正方形,深度为2.5m的长方体无盖蓄水池,建造池壁的单价是120元/m2,建造池底的单价是240元/m2,总造价是8640元,求池底的边长.
分析:池底的造价+池壁的造价=总造价
解:设池底的边长是xm.
根据题意得:
解方程得:
∵池底的边长不能为负数,∴取x=4
答:池底的边长是4m.
练习、建造成一个长方体形的水池,原计划水池深3米,水池周围为1400米,经过研讨,修改原方案,要把长与宽两边都增加原方案中的宽的2倍,于是新方案的水池容积为270万米3,求原来方案的水池的长与宽各是多少米?
700--x
x
3
700-x+2x
x+2x
x
原方案
新方案
课堂练习:列方程解下列应用题
1、学生会准备举办一次摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶嵌上一圈等宽的彩纸。经试验,彩纸面积为相片面积的2/3时较美观,求镶上彩纸条的宽。(精确到0.1厘米)
2、在宽20米,长32米的矩形地面上修筑同样宽的四条互相垂直的“井”字形道路(如图),余下的部分做绿地,要使绿地面积为448平方
米,路宽为多少?
32
20
3、小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子。如果要求长方体的底面面积为81平方厘米,那么剪去的正方形边长为多少?
4、学校课外生物(小组的试验园地是一块长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小路(如图),要使种植面积为600平方米,求小道的宽。(精确到0.1米)
5、
在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框。已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm2,求这个长方形框的框边宽。
X
X
30cm
20cm
解:设长方形框的边宽为xcm,依题意,得
30×20–(30–2x)(20–2x)=400
整理得
x2–
25+100=0
得
x1=20,
x2=5
当=20时,20-2x=
-20(舍去);当x=5时,20-2x=10
答:这个长方形框的框边宽为5cm
列一元二次方程解应题
6、放铅笔的V形槽如图,每往上一层可以多
放一支铅笔.现有190支铅笔,则要放几层
?
解:要放x层,则每一层放(1+x)
支铅笔.得
x
(1+x)
=190×2
X+
X
-380=0
解得X1=19,
X2=
-
20(不合题意)
答:要放19层.
2
列一元二次方程解应题
补充练习:
(98年北京市崇文区中考题)如图,有一面
积是150平方米的长方形鸡场,鸡场的一边靠墙
(墙长18米),墙对面有一个2米宽的门,另三边
(门除外)用竹篱笆围成,篱笆总长33米.求鸡
场的长和宽各多少米?
四、利润问题:总利润=单件利润
销量
1、爱家超市将进货单价为40元的商品,按50元销售时,能卖出500个,已知该商品每涨1元钱就少卖10个。为了赚8000元的利润,应涨多少元钱?
2、某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,经量减少库存,商场决定适当的降低售价,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件,若商场平均每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价多少元?
3、某商户以2元/千克的价格,购进一批小西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该商户决定降价出售,经调查发现,这种小西瓜每降价0.1元/千克,每天可多售出40千克,另外每天的房租等固定成本共24元,该商户要想每天盈利200元,应该将每千克的小西瓜的售价降低多少元?
五、球赛问题:(握手、签合同、打电话、送礼)
要组织一场篮球联赛,赛制为单循环形式(每两个队只赛一场)。计划安排15场比赛,应邀请多少个球队参加比赛?
参加一次聚会的每两个人都握了一次手,所有人共握手36次,有多少人参加聚会?
六、数字问题:
1.一个两位数,十位数字与个位数字之和为5,把这个数的十位数字与个位数字对调后,所得的新两位数与原两位数乘积为736,求原两位数。
2、有一个两位数,它的个位上的数字与十位上的数字之和是6,如果把它的个位数字与十位数字调换位置,所得的两位数乘以原来的两位数所得的积等于1008,求调换位置后得到的两位数。
同课章节目录
