人教版数学八年级上册第十一章 三角形 11.3 多边形及其内角和 同步练习(word版,含答案)
文档属性
| 名称 | 人教版数学八年级上册第十一章 三角形 11.3 多边形及其内角和 同步练习(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览


文档简介
多边形及其内角和
同步练习
一.选择题(共12小题)
1.一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360°
B.外角和增加360°
C.内角和增加180°
D.对角线增加一条
2.如果n边形的每一个内角都等于与它相邻外角的2倍,那么n的值是( )
A.7
B.6
C.5
D.4
3.若一个n边形的内角和是1620°,则n的值为( )
A.9B.10C.11D.12
4.已知一个正多边形的内角为a度,则下列不可能是a的值的是( )
A.90
B.100
C.120
D.176.4
5.如图,足球图片中的一块白色皮块的内角和是( )
A.180°
B.360°
C.540°
D.720°
6.如图在五边形ABCDE中,∠A=∠B=∠C=∠D,∠DEF=3∠AEF,则∠AFE度数是( )
A.45°
B.60°
C.72°
D.无法确定
7.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1:3,则这个多边形为( )
A.三角形
B.四边形
C.六边形
D.八边形
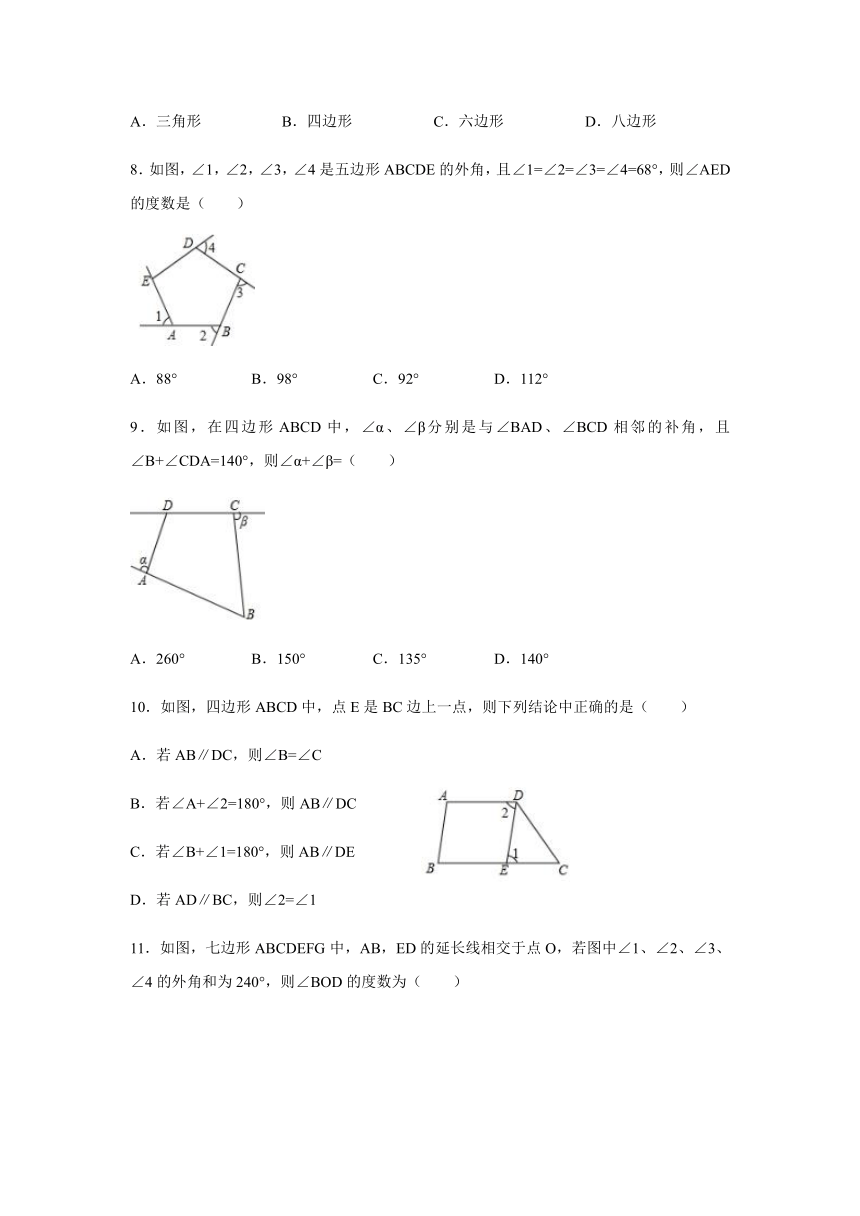
8.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=68°,则∠AED的度数是( )
A.88°
B.98°
C.92°
D.112°
9.如图,在四边形ABCD中,∠α、∠β分别是与∠BAD、∠BCD相邻的补角,且∠B+∠CDA=140°,则∠α+∠β=( )
A.260°
B.150°
C.135°
D.140°
10.如图,四边形ABCD中,点E是BC边上一点,则下列结论中正确的是( )
A.若AB∥DC,则∠B=∠C
B.若∠A+∠2=180°,则AB∥DC
C.若∠B+∠1=180°,则AB∥DE
D.若AD∥BC,则∠2=∠1
11.如图,七边形ABCDEFG中,AB,ED的延长线相交于点O,若图中∠1、∠2、∠3、∠4的外角和为240°,则∠BOD的度数为( )
A.40°
B.45°
C.50°
D.60°
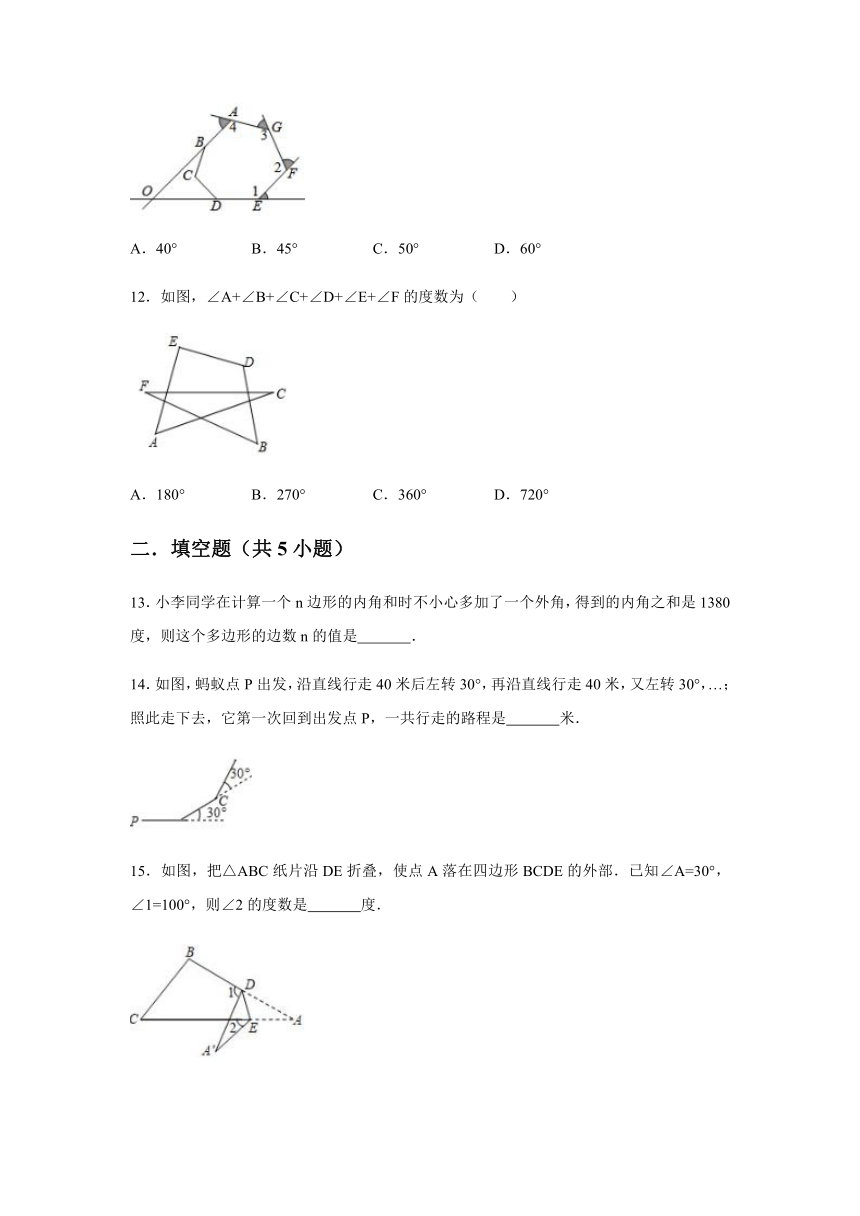
12.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180°
B.270°
C.360°
D.720°
二.填空题(共5小题)
13.小李同学在计算一个n边形的内角和时不小心多加了一个外角,得到的内角之和是1380度,则这个多边形的边数n的值是
.
14.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是
米.
15.如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的外部.已知∠A=30°,∠1=100°,则∠2的度数是
度.
16.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,其中∠1+∠2+∠3+∠4=α,若∠BOD=38°,则α的值是
.
17.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=40°,则∠BPC的度数是
.
三.解答题(共5小题)
18.如图,四边形ABCD中,已知∠B、∠C的角平分线相交于点O,∠A+∠D=200°,求∠BOC的度数.
如图所示:求∠A+∠D+∠B+∠E+∠C+∠F的度数.
20.如图所示,直线EF分别交四边形ABDC的边CA与BD的延长线于点M和N,且∠1=∠3,∠B=∠C,∠N=30°.求∠M的度数.
21.如图是两位小朋友在探究某多边形的内角和时的一段对话,请根据他们的对话内容判断他们是在求几边形?少加的内角为多少度?
22.(1)如图1,计算下列五角星图案中五个顶角的度数和.
即:求∠A+∠B+∠C+∠D+∠E的大小.
(2)如图2,若五角星的五个顶角的度数相等,求∠1的大小.
参考答案
1-5;CBCBD
6-10:ADCDD
11-12:DC
13、9
14、480
15、40
16、218°
17、140°
18、四边ABCD中,∠A+∠ABC+∠BCD+∠D=360°
∵∠A+∠D=200°,
∴∠ABC+∠BCD=360°-200°=160°
∵BO、CO分别是∠ABC、∠BCD的平分线,
∠OBC=∠ABC,∠OCB=∠BCD,
∴∠OBC=(∠ABC+∠BCD)=×160°=80°
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-80°=100°,
∴∠BOC的度数为100°
19、由图可得,∠A+∠D+∠B+∠E+∠C+∠F的和正好是中间小三角形的三个外角之和,
∵三角形的外角和是360°,
∴∠A+∠D+∠B+∠E+∠C+∠F=360°.
20、:∵∠1=∠2,∠1=∠3,
∴∠2=∠3(等量代换),
∴AB∥CD(同位角相等,两直线平行),
∴∠MAB=∠C(两直线平行,同位角相等),
又∵∠B=∠C,
∴∠NAB=∠B(等量代换),
∴CM∥BN(内错角相等,两直线平行),
∴∠M=∠N(两直线平行,内错角相等),
∵∠N=30°,
∴∠M=30°.
21、1140°÷180°=6…60°,
则边数是:6+1+2=9;
他们在求九边形的内角和;
180°-60°=120°,
少加的那个内角为120度.
22、:(1)设BD、AD与CE的交点为M、N;
△MBE和△NAC中,由三角形的外角性质知:
∠DMN=∠B+∠E,∠DNM=∠A+∠C;
△DMN中,∠DMN+∠DNM+∠D=180°,
故∠A+∠B+∠C+∠D+∠E=180°;
(2)∵五角星的五个顶角的度数相等,
∴∠2==72°,
∴∠1=180°-∠2=108°.
同步练习
一.选择题(共12小题)
1.一个多边形的边数每增加一条,这个多边形的( )
A.内角和增加360°
B.外角和增加360°
C.内角和增加180°
D.对角线增加一条
2.如果n边形的每一个内角都等于与它相邻外角的2倍,那么n的值是( )
A.7
B.6
C.5
D.4
3.若一个n边形的内角和是1620°,则n的值为( )
A.9B.10C.11D.12
4.已知一个正多边形的内角为a度,则下列不可能是a的值的是( )
A.90
B.100
C.120
D.176.4
5.如图,足球图片中的一块白色皮块的内角和是( )
A.180°
B.360°
C.540°
D.720°
6.如图在五边形ABCDE中,∠A=∠B=∠C=∠D,∠DEF=3∠AEF,则∠AFE度数是( )
A.45°
B.60°
C.72°
D.无法确定
7.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1:3,则这个多边形为( )
A.三角形
B.四边形
C.六边形
D.八边形
8.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=68°,则∠AED的度数是( )
A.88°
B.98°
C.92°
D.112°
9.如图,在四边形ABCD中,∠α、∠β分别是与∠BAD、∠BCD相邻的补角,且∠B+∠CDA=140°,则∠α+∠β=( )
A.260°
B.150°
C.135°
D.140°
10.如图,四边形ABCD中,点E是BC边上一点,则下列结论中正确的是( )
A.若AB∥DC,则∠B=∠C
B.若∠A+∠2=180°,则AB∥DC
C.若∠B+∠1=180°,则AB∥DE
D.若AD∥BC,则∠2=∠1
11.如图,七边形ABCDEFG中,AB,ED的延长线相交于点O,若图中∠1、∠2、∠3、∠4的外角和为240°,则∠BOD的度数为( )
A.40°
B.45°
C.50°
D.60°
12.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180°
B.270°
C.360°
D.720°
二.填空题(共5小题)
13.小李同学在计算一个n边形的内角和时不小心多加了一个外角,得到的内角之和是1380度,则这个多边形的边数n的值是
.
14.如图,蚂蚁点P出发,沿直线行走40米后左转30°,再沿直线行走40米,又左转30°,…;照此走下去,它第一次回到出发点P,一共行走的路程是
米.
15.如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的外部.已知∠A=30°,∠1=100°,则∠2的度数是
度.
16.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,其中∠1+∠2+∠3+∠4=α,若∠BOD=38°,则α的值是
.
17.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=40°,则∠BPC的度数是
.
三.解答题(共5小题)
18.如图,四边形ABCD中,已知∠B、∠C的角平分线相交于点O,∠A+∠D=200°,求∠BOC的度数.
如图所示:求∠A+∠D+∠B+∠E+∠C+∠F的度数.
20.如图所示,直线EF分别交四边形ABDC的边CA与BD的延长线于点M和N,且∠1=∠3,∠B=∠C,∠N=30°.求∠M的度数.
21.如图是两位小朋友在探究某多边形的内角和时的一段对话,请根据他们的对话内容判断他们是在求几边形?少加的内角为多少度?
22.(1)如图1,计算下列五角星图案中五个顶角的度数和.
即:求∠A+∠B+∠C+∠D+∠E的大小.
(2)如图2,若五角星的五个顶角的度数相等,求∠1的大小.
参考答案
1-5;CBCBD
6-10:ADCDD
11-12:DC
13、9
14、480
15、40
16、218°
17、140°
18、四边ABCD中,∠A+∠ABC+∠BCD+∠D=360°
∵∠A+∠D=200°,
∴∠ABC+∠BCD=360°-200°=160°
∵BO、CO分别是∠ABC、∠BCD的平分线,
∠OBC=∠ABC,∠OCB=∠BCD,
∴∠OBC=(∠ABC+∠BCD)=×160°=80°
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-80°=100°,
∴∠BOC的度数为100°
19、由图可得,∠A+∠D+∠B+∠E+∠C+∠F的和正好是中间小三角形的三个外角之和,
∵三角形的外角和是360°,
∴∠A+∠D+∠B+∠E+∠C+∠F=360°.
20、:∵∠1=∠2,∠1=∠3,
∴∠2=∠3(等量代换),
∴AB∥CD(同位角相等,两直线平行),
∴∠MAB=∠C(两直线平行,同位角相等),
又∵∠B=∠C,
∴∠NAB=∠B(等量代换),
∴CM∥BN(内错角相等,两直线平行),
∴∠M=∠N(两直线平行,内错角相等),
∵∠N=30°,
∴∠M=30°.
21、1140°÷180°=6…60°,
则边数是:6+1+2=9;
他们在求九边形的内角和;
180°-60°=120°,
少加的那个内角为120度.
22、:(1)设BD、AD与CE的交点为M、N;
△MBE和△NAC中,由三角形的外角性质知:
∠DMN=∠B+∠E,∠DNM=∠A+∠C;
△DMN中,∠DMN+∠DNM+∠D=180°,
故∠A+∠B+∠C+∠D+∠E=180°;
(2)∵五角星的五个顶角的度数相等,
∴∠2==72°,
∴∠1=180°-∠2=108°.
