苏科版数学八年级上册《第3章 勾股定理》 单元练习(Word版 含答案)
文档属性
| 名称 | 苏科版数学八年级上册《第3章 勾股定理》 单元练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 141.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 14:02:22 | ||
图片预览


文档简介
第3章
勾股定理
一.选择题(共8小题,满分24分,每小题3分)
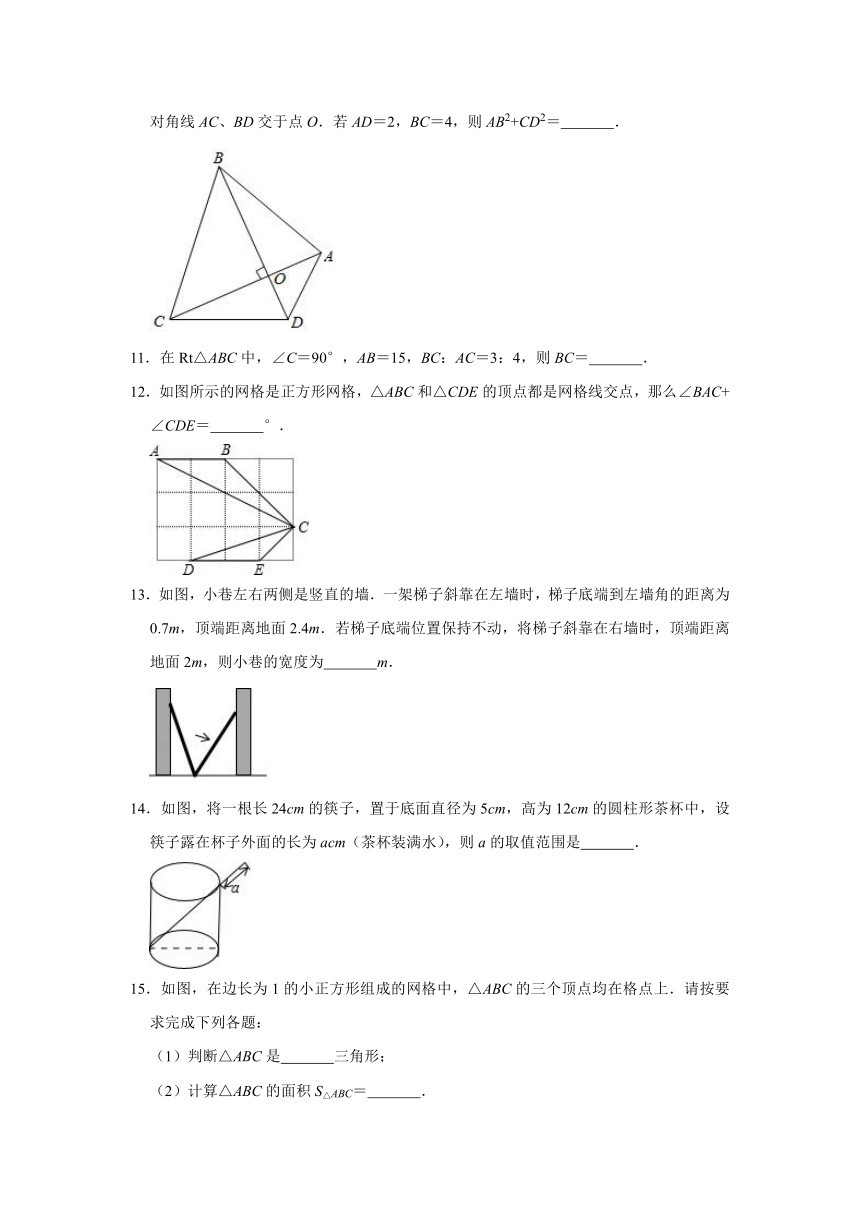
1.下列各组数中,能构成直角三角形的是( )
A.4,5,6
B.1,1,
C.6,8,11
D.5,12,23
2.下列命题中是假命题的是( )
A.角平分线上的点到角两边的距离相等
B.位似变换不改变图形的形状和大小
C.等腰三角形两底角相等
D.直角三角形斜边上的中线等于斜边的一半
3.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13
B.26
C.34
D.47
4.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是32,则图中阴影部分面积等于( )
A.16
B.8
C.4
D.2
5.如图字母B所代表的正方形的面积是( )
A.12
B.13
C.144
D.194
6.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A.13cm
B.cm
C.2cm
D.20cm
7.△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A.△ABC的周长
B.△AFH的周长
C.四边形FBGH的周长
D.四边形ADEC的周长
8.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )
A.4
B.8
C.16
D.64
二.填空题(共8小题,满分24分,每小题3分)
9.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要
元钱.
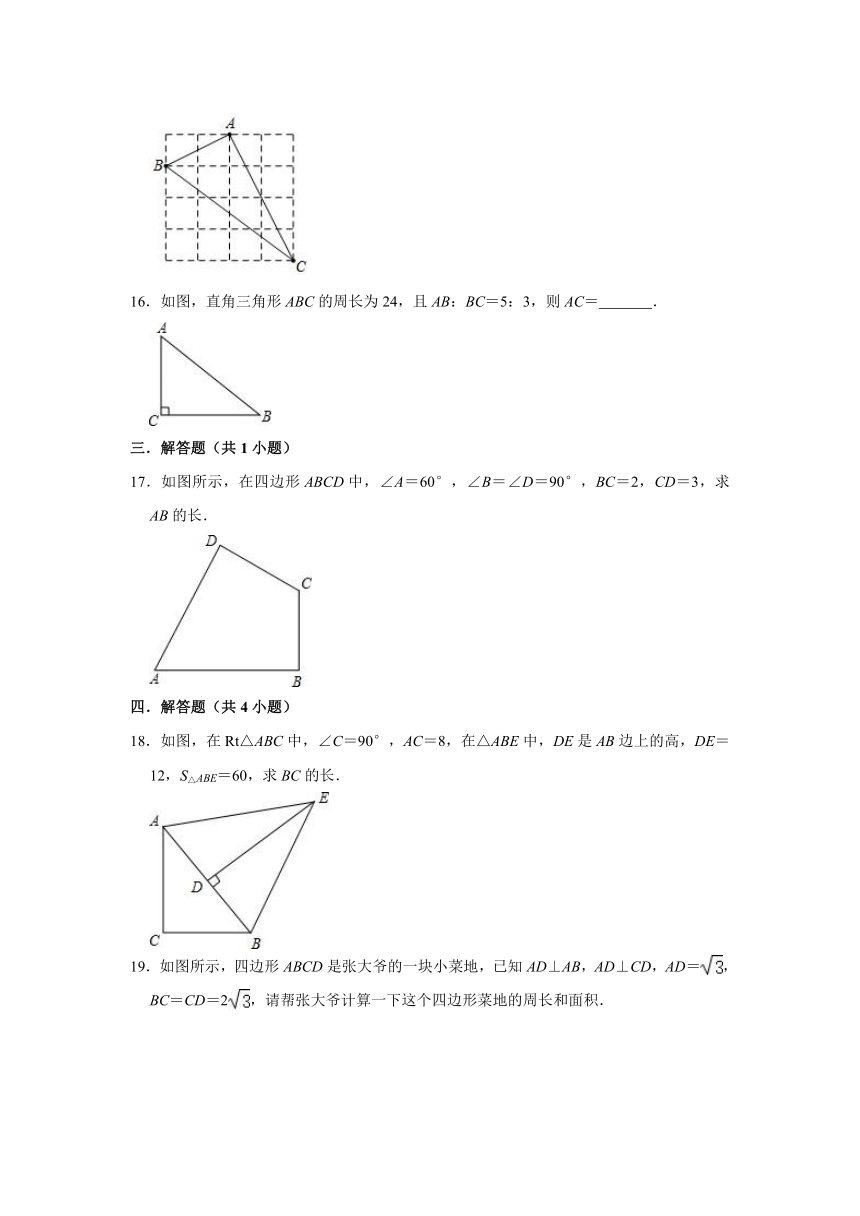
10.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2=
.
11.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC=
.
12.如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE=
°.
13.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为
m.
14.如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是
.
15.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求完成下列各题:
(1)判断△ABC是
三角形;
(2)计算△ABC的面积S△ABC=
.
16.如图,直角三角形ABC的周长为24,且AB:BC=5:3,则AC=
.
三.解答题(共1小题)
17.如图所示,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.
四.解答题(共4小题)
18.如图,在Rt△ABC中,∠C=90°,AC=8,在△ABE中,DE是AB边上的高,DE=12,S△ABE=60,求BC的长.
19.如图所示,四边形ABCD是张大爷的一块小菜地,已知AD⊥AB,AD⊥CD,AD=,BC=CD=2,请帮张大爷计算一下这个四边形菜地的周长和面积.
20.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
21.图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的端点均在格点上,在图②、图③中仿照图①,只用无刻度的直尺,各画出一条线段CD,将线段AB分为2:3两部分.
要求:所画线段CD的位置不同,点C、D均在格点上
参考答案
一.选择题
1.
B.
2.
B.
3.
D.
4.B.
5.
C.
6.
D.
7.
A.
8.
D.
二.填空题
9.612.
10.
20.
11.
9.
12.
45°.
13.
2.2.
14.
11cm≤a≤12cm.
15.
5.
16.
8.
三.解答题
17.解:如下图:延长AD、BC交于E点,
∵∠A=60°,
∴∠E=90°﹣60°=30°.
∵CD=3,
∴CE=3×2=6,
则BE=2+6=8.
∴AB=.
四.解答题(共4小题)
18.解:如图,∵在△ABE中,DE是AB边上的高,DE=12,S△ABE=60,
∴AB?ED=60,即AB×12=60,
解得AB=10.
又∵在Rt△ABC中,∠C=90°,AC=8,
∴BC==6.
答:线段BC的长度是6.
19.解:如图,作CE⊥AB于E.
∵AD⊥AB,AD⊥CD,
∴∠A=∠D=∠AEC=90°,
∴四边形AECD是矩形,
∴AD=CE=,CD=AE=2,
在Rt△BCE中,BE===3,
∴AB=AE+BE=2+3,
∴四边形ABCD的周长=+2+2+2+3=7+3,
四边形ABCD的面积=?=.
20.解:(2)因为S△ABC=S△ABI+S△BIC+S△AIC
=cx+ax+bx
所以x=.
答:x与a、b、c的关系为x=.
(3)根据(1)和(2)得:
x==.
即2ab=(a+b+c)(a+b﹣c)
化简得a2+b2=c2.
21.解:如图所示:
图中各画出了一条线段CD,将线段AB分为2:3两部分.
勾股定理
一.选择题(共8小题,满分24分,每小题3分)
1.下列各组数中,能构成直角三角形的是( )
A.4,5,6
B.1,1,
C.6,8,11
D.5,12,23
2.下列命题中是假命题的是( )
A.角平分线上的点到角两边的距离相等
B.位似变换不改变图形的形状和大小
C.等腰三角形两底角相等
D.直角三角形斜边上的中线等于斜边的一半
3.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13
B.26
C.34
D.47
4.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是32,则图中阴影部分面积等于( )
A.16
B.8
C.4
D.2
5.如图字母B所代表的正方形的面积是( )
A.12
B.13
C.144
D.194
6.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A.13cm
B.cm
C.2cm
D.20cm
7.△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A.△ABC的周长
B.△AFH的周长
C.四边形FBGH的周长
D.四边形ADEC的周长
8.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )
A.4
B.8
C.16
D.64
二.填空题(共8小题,满分24分,每小题3分)
9.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要
元钱.
10.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2=
.
11.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC=
.
12.如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE=
°.
13.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2m,则小巷的宽度为
m.
14.如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是
.
15.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求完成下列各题:
(1)判断△ABC是
三角形;
(2)计算△ABC的面积S△ABC=
.
16.如图,直角三角形ABC的周长为24,且AB:BC=5:3,则AC=
.
三.解答题(共1小题)
17.如图所示,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.
四.解答题(共4小题)
18.如图,在Rt△ABC中,∠C=90°,AC=8,在△ABE中,DE是AB边上的高,DE=12,S△ABE=60,求BC的长.
19.如图所示,四边形ABCD是张大爷的一块小菜地,已知AD⊥AB,AD⊥CD,AD=,BC=CD=2,请帮张大爷计算一下这个四边形菜地的周长和面积.
20.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
21.图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的端点均在格点上,在图②、图③中仿照图①,只用无刻度的直尺,各画出一条线段CD,将线段AB分为2:3两部分.
要求:所画线段CD的位置不同,点C、D均在格点上
参考答案
一.选择题
1.
B.
2.
B.
3.
D.
4.B.
5.
C.
6.
D.
7.
A.
8.
D.
二.填空题
9.612.
10.
20.
11.
9.
12.
45°.
13.
2.2.
14.
11cm≤a≤12cm.
15.
5.
16.
8.
三.解答题
17.解:如下图:延长AD、BC交于E点,
∵∠A=60°,
∴∠E=90°﹣60°=30°.
∵CD=3,
∴CE=3×2=6,
则BE=2+6=8.
∴AB=.
四.解答题(共4小题)
18.解:如图,∵在△ABE中,DE是AB边上的高,DE=12,S△ABE=60,
∴AB?ED=60,即AB×12=60,
解得AB=10.
又∵在Rt△ABC中,∠C=90°,AC=8,
∴BC==6.
答:线段BC的长度是6.
19.解:如图,作CE⊥AB于E.
∵AD⊥AB,AD⊥CD,
∴∠A=∠D=∠AEC=90°,
∴四边形AECD是矩形,
∴AD=CE=,CD=AE=2,
在Rt△BCE中,BE===3,
∴AB=AE+BE=2+3,
∴四边形ABCD的周长=+2+2+2+3=7+3,
四边形ABCD的面积=?=.
20.解:(2)因为S△ABC=S△ABI+S△BIC+S△AIC
=cx+ax+bx
所以x=.
答:x与a、b、c的关系为x=.
(3)根据(1)和(2)得:
x==.
即2ab=(a+b+c)(a+b﹣c)
化简得a2+b2=c2.
21.解:如图所示:
图中各画出了一条线段CD,将线段AB分为2:3两部分.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
