北师大版数学九年级上册2.6 应用一元二次方程(第1课时 利用一元二次方程求解几何问题)课件(共20张PPT)
文档属性
| 名称 | 北师大版数学九年级上册2.6 应用一元二次方程(第1课时 利用一元二次方程求解几何问题)课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 17:37:15 | ||
图片预览








文档简介
北师大版数学九年级上册
第二章 一元二次方程
2.6 应用一元二次方程
第1课时 利用一元二次方程求解几何问题
1.使学生会用一元二次方程解应用题.
2.进一步培养学生将实际问题转化为数学问题的能力和分析问题、解决问题的能力,培养学生运用数学的意识.
3.通过列方程解应用题,进一步体会运用代数中方程的思想方法解应用题的优越性.
学习目标
1.在Rt△ACB中,∠C=90°,AC=5cm,
BC=12cm,则AB=_____cm.
2.在△ABC中,D、E分别是AB,AC的中点,
若BC=10cm,则DE= _____ cm.
13
5
回顾旧知
3.用一根长40cm的铁丝围成一个面积为91cm2的矩形,问这个矩形长是多少?
解:设长为xcm,则宽为
解这个方程,得x1=7,x2=13.当x=7cm时,
当x=13cm时,
∴这个矩形的长为13cm.
知识模块 探究教材P52例1
(一)自主探究
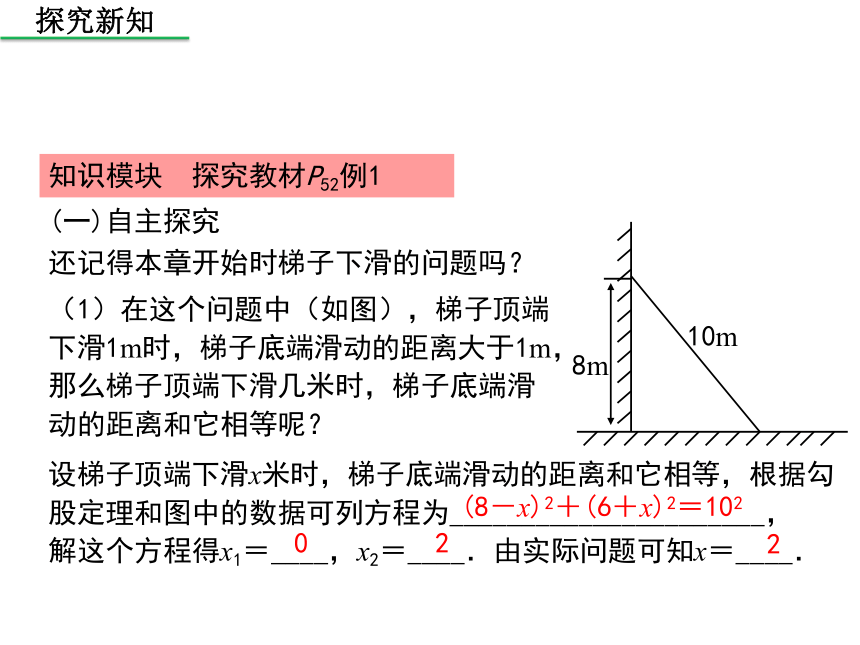
还记得本章开始时梯子下滑的问题吗?
(1)在这个问题中(如图),梯子顶端下滑1m时,梯子底端滑动的距离大于1m,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
10m
8m
设梯子顶端下滑x米时,梯子底端滑动的距离和它相等,根据勾股定理和图中的数据可列方程为______________________,
解这个方程得x1=____,x2=____.由实际问题可知x=____.
(8-x)2+(6+x)2=102
0
2
2
探究新知
(2)如果梯子长度是13m,梯子顶端与地面的垂直距离为12m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
设梯子顶端下滑x米时,梯子底端滑动的距离和它相等,根据勾股定理和已知数据可列方程为______________________,解这个方程得x1=_____,x2=_____,由实际问题可知x=_____.
(12-x)2+(5+x)2=132
0
7
7
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里,其中 )
例
如图,某海军基地位于A处,在其正南方向200n?mile 处有
一目标B,在B的正东方向200n?mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品
送达军舰.
A
B
D
C
E
F
北
东
200
200
45°
(二)合作探究
∵AD=CD BF=CF
解:连接DF,
∴DF是△ABC的中位线
∵DF//AB且DF= AB
∵AB┴BC AB=BC=200
∴DF┴BC DF=100(海里)BF=100(海里)
A
B
D
C
E
F
北
东
200
?
200
45°
若设相遇时补给船的行程DE为x海里,则相遇时军舰的行程应为AB+BE=2 x海里.
EF=AB+BF-(AB+BE) =(300-2 x)海里
答:相遇时补给船航行了约118.4海里.
(不合题意,舍去)
整理得
解这个方程得
该部分是学习中的难点,要去审清题意,分析各量之间的关系,不能粗线条解决.在讲解过程中可逐步分解难点:
①审清题意;
②找准各条有关线段的长度关系;
③建立方程模型,之后求解.
解决实际应用问题的关键是审清题意,自己反复审题,弄清各量之间的关系,分析题目中的已知条件和要求解的问题,并在这个前提下抓住图形中各条线段所表示的量,弄清它们之间的关系.在分析题意遇到困难时,可设置问题串分解难点:
(1)要求DE的长,需要如何设未知数?
(2)怎样建立含DE未知数的等量关系?从已知条件中能找到吗?
(3)利用勾股定理建立等量关系,如何构造直角三角形?
(4)选定Rt△DEF后,三条边长都是已知的吗?DE,DF,EF分别是多少?
在问题串的引导下,逐层分析,在分组讨论后找出题目中的等量关系即:
速度等量:V军舰=2×V补给船;时间等量:t军舰=t补给船;
三边数量关系:EF2+FD2=DE2.
弄清图形中线段长表示的量:已知AB=BC=200海里,DE表示补给船的路程,AB+BE表示军舰的路程.
在此基础上选准未知数,用未知数表示出线段DE、EF的长,根据勾股定理列方程求解,并判断解的合理性.
练习
1.一个直角三角形的斜边长为7cm,一条直角边比另一条直角边长1cm,那么这个直角三角形的面积是多少?
解:设较短直角边长为xcm,由题意,得:
x2+(x+1)2=72,化简得:x2+x-24=0.
∴较长直角边长为
∴直角三角形面积=
解这个方程得:
2.在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路(两条纵向,一条横向,横向与纵向互相垂直)(如图1),把耕地分成大小相等的六块作试验田,要使试验田面积为570平方米,问道路应为多宽?
图(1)
解:设道路宽为x米,
如图(2)利用平移知识可列方程为
(32-2x)(20-x)=570,
化简得x2-36x+35=0,
解这个方程得x1=1,x2=35>32(不合题意,舍去),
∴道路宽应为1米.
图(2)
1.用长为100cm的金属丝制成一个矩形框子,框子的面积不可能是( )
A.375cm2 B.500cm2
C.625cm2 D.700cm2
D
课堂练习
2.一块矩形耕地大小尺寸如图所示,要在这块耕地上沿东西和南北方向分别挖两条和四条水渠,如果水渠的宽相等,而且要保证余下的可耕地面积为9600m2,那么水渠的宽为( )
A.2m B.4m
C.1m D.3m
C
3.一个矩形的面积是48平方厘米,它的长比宽多8厘米,设矩形的宽x厘米,应满足方程______________.解方程求得x=_____.
x(x+8)=48
4
4.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.
求该矩形草坪BC边的长.
解:设该矩形草坪BC边的长为x,则
得x1=20(舍去),x2=12.
∴该矩形草坪BC边长为12米.
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?已,未知之间有什么关系?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完事的语句,注明单位且要贴近生活.
总结新知
第二章 一元二次方程
2.6 应用一元二次方程
第1课时 利用一元二次方程求解几何问题
1.使学生会用一元二次方程解应用题.
2.进一步培养学生将实际问题转化为数学问题的能力和分析问题、解决问题的能力,培养学生运用数学的意识.
3.通过列方程解应用题,进一步体会运用代数中方程的思想方法解应用题的优越性.
学习目标
1.在Rt△ACB中,∠C=90°,AC=5cm,
BC=12cm,则AB=_____cm.
2.在△ABC中,D、E分别是AB,AC的中点,
若BC=10cm,则DE= _____ cm.
13
5
回顾旧知
3.用一根长40cm的铁丝围成一个面积为91cm2的矩形,问这个矩形长是多少?
解:设长为xcm,则宽为
解这个方程,得x1=7,x2=13.当x=7cm时,
当x=13cm时,
∴这个矩形的长为13cm.
知识模块 探究教材P52例1
(一)自主探究
还记得本章开始时梯子下滑的问题吗?
(1)在这个问题中(如图),梯子顶端下滑1m时,梯子底端滑动的距离大于1m,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
10m
8m
设梯子顶端下滑x米时,梯子底端滑动的距离和它相等,根据勾股定理和图中的数据可列方程为______________________,
解这个方程得x1=____,x2=____.由实际问题可知x=____.
(8-x)2+(6+x)2=102
0
2
2
探究新知
(2)如果梯子长度是13m,梯子顶端与地面的垂直距离为12m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
设梯子顶端下滑x米时,梯子底端滑动的距离和它相等,根据勾股定理和已知数据可列方程为______________________,解这个方程得x1=_____,x2=_____,由实际问题可知x=_____.
(12-x)2+(5+x)2=132
0
7
7
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里,其中 )
例
如图,某海军基地位于A处,在其正南方向200n?mile 处有
一目标B,在B的正东方向200n?mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品
送达军舰.
A
B
D
C
E
F
北
东
200
200
45°
(二)合作探究
∵AD=CD BF=CF
解:连接DF,
∴DF是△ABC的中位线
∵DF//AB且DF= AB
∵AB┴BC AB=BC=200
∴DF┴BC DF=100(海里)BF=100(海里)
A
B
D
C
E
F
北
东
200
?
200
45°
若设相遇时补给船的行程DE为x海里,则相遇时军舰的行程应为AB+BE=2 x海里.
EF=AB+BF-(AB+BE) =(300-2 x)海里
答:相遇时补给船航行了约118.4海里.
(不合题意,舍去)
整理得
解这个方程得
该部分是学习中的难点,要去审清题意,分析各量之间的关系,不能粗线条解决.在讲解过程中可逐步分解难点:
①审清题意;
②找准各条有关线段的长度关系;
③建立方程模型,之后求解.
解决实际应用问题的关键是审清题意,自己反复审题,弄清各量之间的关系,分析题目中的已知条件和要求解的问题,并在这个前提下抓住图形中各条线段所表示的量,弄清它们之间的关系.在分析题意遇到困难时,可设置问题串分解难点:
(1)要求DE的长,需要如何设未知数?
(2)怎样建立含DE未知数的等量关系?从已知条件中能找到吗?
(3)利用勾股定理建立等量关系,如何构造直角三角形?
(4)选定Rt△DEF后,三条边长都是已知的吗?DE,DF,EF分别是多少?
在问题串的引导下,逐层分析,在分组讨论后找出题目中的等量关系即:
速度等量:V军舰=2×V补给船;时间等量:t军舰=t补给船;
三边数量关系:EF2+FD2=DE2.
弄清图形中线段长表示的量:已知AB=BC=200海里,DE表示补给船的路程,AB+BE表示军舰的路程.
在此基础上选准未知数,用未知数表示出线段DE、EF的长,根据勾股定理列方程求解,并判断解的合理性.
练习
1.一个直角三角形的斜边长为7cm,一条直角边比另一条直角边长1cm,那么这个直角三角形的面积是多少?
解:设较短直角边长为xcm,由题意,得:
x2+(x+1)2=72,化简得:x2+x-24=0.
∴较长直角边长为
∴直角三角形面积=
解这个方程得:
2.在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路(两条纵向,一条横向,横向与纵向互相垂直)(如图1),把耕地分成大小相等的六块作试验田,要使试验田面积为570平方米,问道路应为多宽?
图(1)
解:设道路宽为x米,
如图(2)利用平移知识可列方程为
(32-2x)(20-x)=570,
化简得x2-36x+35=0,
解这个方程得x1=1,x2=35>32(不合题意,舍去),
∴道路宽应为1米.
图(2)
1.用长为100cm的金属丝制成一个矩形框子,框子的面积不可能是( )
A.375cm2 B.500cm2
C.625cm2 D.700cm2
D
课堂练习
2.一块矩形耕地大小尺寸如图所示,要在这块耕地上沿东西和南北方向分别挖两条和四条水渠,如果水渠的宽相等,而且要保证余下的可耕地面积为9600m2,那么水渠的宽为( )
A.2m B.4m
C.1m D.3m
C
3.一个矩形的面积是48平方厘米,它的长比宽多8厘米,设矩形的宽x厘米,应满足方程______________.解方程求得x=_____.
x(x+8)=48
4
4.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.
求该矩形草坪BC边的长.
解:设该矩形草坪BC边的长为x,则
得x1=20(舍去),x2=12.
∴该矩形草坪BC边长为12米.
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?已,未知之间有什么关系?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完事的语句,注明单位且要贴近生活.
总结新知
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
