9.7同底数幂的乘法-沪教版(上海)七年级数学上册课件(31张)
文档属性
| 名称 | 9.7同底数幂的乘法-沪教版(上海)七年级数学上册课件(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 846.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 17:38:43 | ||
图片预览










文档简介
(共31张PPT)
9.7
同底数幂的乘法
教学目标:
1.理解同底数幂的乘法的性质的推导过程;
2.能运用性质来解答一些变式练习;
3.能运用性质来解决一些实际问题.
复习:
1.
103的意义:
10×10×10
10的三次方
读作:
10的立方
2.
a3的意义:
a·a·a
a的三次方
读作:
a的立方
3.
an的意义:
a的n次方
读作:
其中a表示
,正整数n表示
,
a的n次乘方的结果叫做
.
a的n次幂
底数
指数
口答
指出下列各幂的底数和指数:
(1)103;
(2)
;
(3)
;
(4)
.
如何计算?
两个幂的底数相同
请把结果写成幂的形式:
新知探索
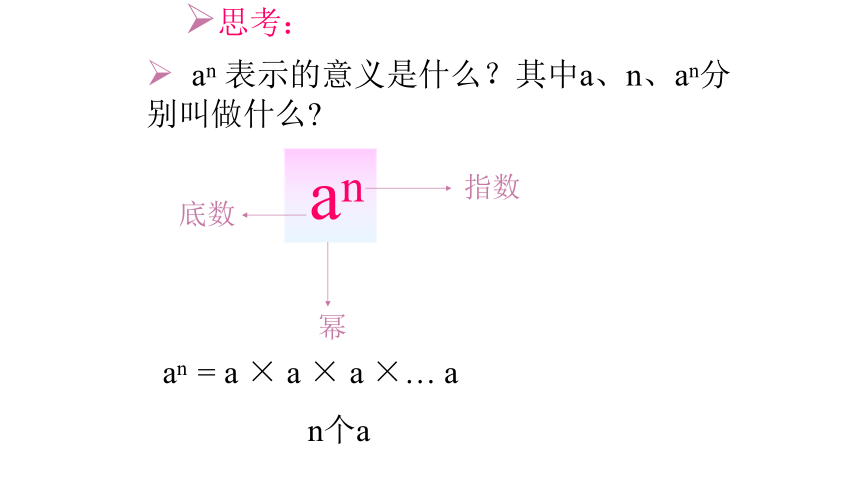
an
表示的意义是什么?其中a、n、an分
别叫做什么?
an
底数
幂
指数
思考:
an
=
a
×
a
×
a
×…
a
n个a
25表示什么?
10×10×10×10×10
可以写成什么形式?
问题:
25
=
.
?
2×2×2×2×2
105
10×10×10×10×10
=
.
(乘方的意义)
(乘方的意义)
式子103×102的意义是什么?
思考:
103与102
的积
底数相同
这个式子中的两个因式有何特点?
请同学们先根据自己的理解,解答下列各题.
103
×102
=(10×10×10)×(10×10)
=
10(
)
23
×22
=
=2(
)
5
(2×2×2)×(2×2)
5
a3×a2
=
=
a(
)
.
5
(a
a
a)
(a
a)
=2×2×2×2×2
=
a
a
a
a
a
3个a
2个a
5个a
思考:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103
×102
=
10(
)
23
×22
=
2(
)
a3×
a2
=
a(
)
5
5
5
猜想:
am
·
an=
?
(当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确.
3+2
3+2
3+2
=
10(
);
=
2(
);
=
a(
)
。
回到小结
猜想:
am
·
an=
(当m、n都是正整数)
am
·
an
=
m个a
n个a
=
aa…a
=am+n
(m+n)个a
即
am
·
an
=
am+n
(当m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
同底数幂相乘的法则:
同底数幂相乘,底数不变,指数相加.
(m、n都是正整数)
(m、n
、p都是正整数)
一般地:
当有三个或三个以上同底数幂相乘时,以上法则依然适用:
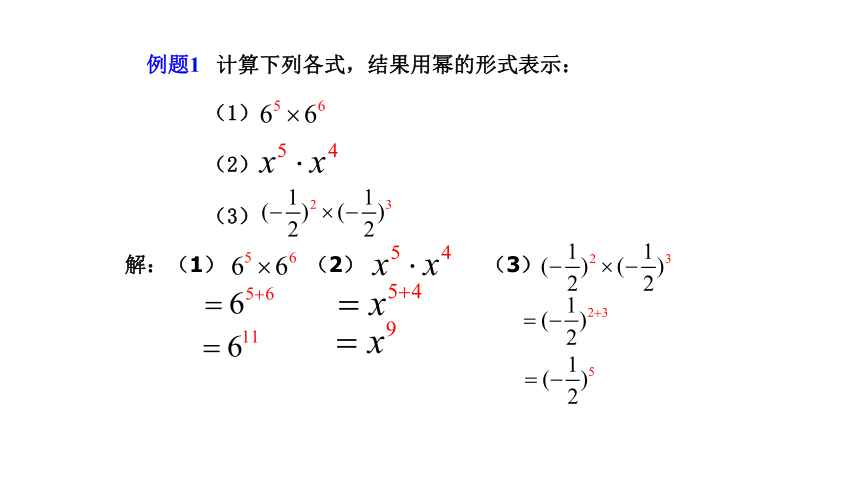
例题1
计算下列各式,结果用幂的形式表示:
(1)
(2)
(3)
解:(1)
(2)
(3)
例题1
计算下列各式,结果用幂的形式表示:
(4)
(5)
(6)
(4)
(5)
1
(6)
课内练习1
判断下列计算是否正确?错误的请改正.
(1)
(2)
(3)
(4)
(5)
(6)
错误
错误
错误
错误
正确
错误
1.计算:
(1)107
×104
;
(2)x2
·
x5
.
解:(1)107
×104
=107
+
4=
1011
(2)x2
·
x5
=
x2
+
5
=
x7
2.计算:(1)23×24×25
(2)y
·
y2
·
y3
解:(1)23×24×25=23+4+5=212
(2)y
·
y2
·
y3
=
y1+2+3=y6
尝试练习
am
·
an
=
am+n
(当m、n都是正整数)
am·an·ap
=
am+n+p
(m、n、p都是正整数)
回到小结
练习一
1.???计算:(抢答)
(1011
)
(
a10
)
(
x10
)
(
b6
)
(2)
a7
·a3
(3)
x5
·x5
(4)
b5
·
b
(1)
105×106
Good!
回顾旧知
在下列各小题的横线上,填上适当的正负号:
从上述练习中你能得到什么规律?
-
-
+
+
探索新知
尝试计算:
探索新知
计算:
(1)解:
或
探索新知
试一试:
在下列各小题的横线上,填上适当的正负号:
-
+
-
+
探索新知
把下列各式化成
的形式:
注意:
1、
幂的指数为1,是省略不写,不要误认为没有指数;
2、结果以幂的形式表示时,要成(-3)的形式,而不是-3
的形式。
3、计算时,幂的结果比较小时,一般计算出来;
练习2
计算下列各式,结果用幂的形式表示:
(1)
(2)
(3)
(4)
(5)
(6)
底数分别是什么?
这个结果是幂的形式吗?
课堂练习:
练习3
计算下列各式,结果用幂的形式表示:
(1)
(2)
2.??计算:
(1)x10
·
x
(2)10×102×104
(3)
x5
·x
·x3
(4)y4·y3·y2·y
解:
(1)x10
·x
=
x10+1=
x11
(2)10×102×104
=101+2+4
=107
(3)x5
·x
·x3
=
x5+1+3
=
x9
(4)y4
·y3
·y2
·y=
y4+3+2+1=
y10
练习二
下面的计算对不对?如果不对,怎样改正?
(1)b5
·
b5=
2b5
(
)
(2)b5
+
b5
=
b10
(
)
(3)x5
·x5
=
x25
(
)
(4)y5
·
y5
=
2y10
(
)
(5)c
·
c3
=
c3
(
)
(6)m
+
m3
=
m4
(
)
m
+
m3
=
m
+
m3
b5
·
b5=
b10
b5
+
b5
=
2b5
x5
·
x5
=
x10
y5
·
y5
=y10
c
·
c3
=
c4
×
×
×
×
×
×
了不起!
填空:
(1)x5
·(
)= x
8
(2)a
·(
)= a6
(3)x
·
x3(
)=
x7
(4)xm
·(
)=x3m
变式训练
x3
a5
x3
x2m
真棒!
真不错!
你真行!
太棒了!
思考题
(1)
x
n
·
xn+1
;
(2)
(x+y)3
·
(x+y)4
.
1.计算:
解:
x
n
·
xn+1
=
解:
(x+y)3
·
(x+y)4
=
am
·
an
=
am+n
xn+(n+1)
=
x2n+1
公式中的a可代表一个数、字母、式子等.
(x+y)3+4
=(x+y)7
2.填空:
(1)
8
=
2x,则
x
=
;
(2)
8×
4
=
2x,则
x
=
;
(3)
3×27×9
=
3x,则
x
=
.
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
同底数幂相乘,
底数
指数
am
·
an
=
am+n
(m、n正整数)
小结
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子
公式
应用
不变,
相加.
再见!
9.7
同底数幂的乘法
教学目标:
1.理解同底数幂的乘法的性质的推导过程;
2.能运用性质来解答一些变式练习;
3.能运用性质来解决一些实际问题.
复习:
1.
103的意义:
10×10×10
10的三次方
读作:
10的立方
2.
a3的意义:
a·a·a
a的三次方
读作:
a的立方
3.
an的意义:
a的n次方
读作:
其中a表示
,正整数n表示
,
a的n次乘方的结果叫做
.
a的n次幂
底数
指数
口答
指出下列各幂的底数和指数:
(1)103;
(2)
;
(3)
;
(4)
.
如何计算?
两个幂的底数相同
请把结果写成幂的形式:
新知探索
an
表示的意义是什么?其中a、n、an分
别叫做什么?
an
底数
幂
指数
思考:
an
=
a
×
a
×
a
×…
a
n个a
25表示什么?
10×10×10×10×10
可以写成什么形式?
问题:
25
=
.
?
2×2×2×2×2
105
10×10×10×10×10
=
.
(乘方的意义)
(乘方的意义)
式子103×102的意义是什么?
思考:
103与102
的积
底数相同
这个式子中的两个因式有何特点?
请同学们先根据自己的理解,解答下列各题.
103
×102
=(10×10×10)×(10×10)
=
10(
)
23
×22
=
=2(
)
5
(2×2×2)×(2×2)
5
a3×a2
=
=
a(
)
.
5
(a
a
a)
(a
a)
=2×2×2×2×2
=
a
a
a
a
a
3个a
2个a
5个a
思考:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103
×102
=
10(
)
23
×22
=
2(
)
a3×
a2
=
a(
)
5
5
5
猜想:
am
·
an=
?
(当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确.
3+2
3+2
3+2
=
10(
);
=
2(
);
=
a(
)
。
回到小结
猜想:
am
·
an=
(当m、n都是正整数)
am
·
an
=
m个a
n个a
=
aa…a
=am+n
(m+n)个a
即
am
·
an
=
am+n
(当m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
同底数幂相乘的法则:
同底数幂相乘,底数不变,指数相加.
(m、n都是正整数)
(m、n
、p都是正整数)
一般地:
当有三个或三个以上同底数幂相乘时,以上法则依然适用:
例题1
计算下列各式,结果用幂的形式表示:
(1)
(2)
(3)
解:(1)
(2)
(3)
例题1
计算下列各式,结果用幂的形式表示:
(4)
(5)
(6)
(4)
(5)
1
(6)
课内练习1
判断下列计算是否正确?错误的请改正.
(1)
(2)
(3)
(4)
(5)
(6)
错误
错误
错误
错误
正确
错误
1.计算:
(1)107
×104
;
(2)x2
·
x5
.
解:(1)107
×104
=107
+
4=
1011
(2)x2
·
x5
=
x2
+
5
=
x7
2.计算:(1)23×24×25
(2)y
·
y2
·
y3
解:(1)23×24×25=23+4+5=212
(2)y
·
y2
·
y3
=
y1+2+3=y6
尝试练习
am
·
an
=
am+n
(当m、n都是正整数)
am·an·ap
=
am+n+p
(m、n、p都是正整数)
回到小结
练习一
1.???计算:(抢答)
(1011
)
(
a10
)
(
x10
)
(
b6
)
(2)
a7
·a3
(3)
x5
·x5
(4)
b5
·
b
(1)
105×106
Good!
回顾旧知
在下列各小题的横线上,填上适当的正负号:
从上述练习中你能得到什么规律?
-
-
+
+
探索新知
尝试计算:
探索新知
计算:
(1)解:
或
探索新知
试一试:
在下列各小题的横线上,填上适当的正负号:
-
+
-
+
探索新知
把下列各式化成
的形式:
注意:
1、
幂的指数为1,是省略不写,不要误认为没有指数;
2、结果以幂的形式表示时,要成(-3)的形式,而不是-3
的形式。
3、计算时,幂的结果比较小时,一般计算出来;
练习2
计算下列各式,结果用幂的形式表示:
(1)
(2)
(3)
(4)
(5)
(6)
底数分别是什么?
这个结果是幂的形式吗?
课堂练习:
练习3
计算下列各式,结果用幂的形式表示:
(1)
(2)
2.??计算:
(1)x10
·
x
(2)10×102×104
(3)
x5
·x
·x3
(4)y4·y3·y2·y
解:
(1)x10
·x
=
x10+1=
x11
(2)10×102×104
=101+2+4
=107
(3)x5
·x
·x3
=
x5+1+3
=
x9
(4)y4
·y3
·y2
·y=
y4+3+2+1=
y10
练习二
下面的计算对不对?如果不对,怎样改正?
(1)b5
·
b5=
2b5
(
)
(2)b5
+
b5
=
b10
(
)
(3)x5
·x5
=
x25
(
)
(4)y5
·
y5
=
2y10
(
)
(5)c
·
c3
=
c3
(
)
(6)m
+
m3
=
m4
(
)
m
+
m3
=
m
+
m3
b5
·
b5=
b10
b5
+
b5
=
2b5
x5
·
x5
=
x10
y5
·
y5
=y10
c
·
c3
=
c4
×
×
×
×
×
×
了不起!
填空:
(1)x5
·(
)= x
8
(2)a
·(
)= a6
(3)x
·
x3(
)=
x7
(4)xm
·(
)=x3m
变式训练
x3
a5
x3
x2m
真棒!
真不错!
你真行!
太棒了!
思考题
(1)
x
n
·
xn+1
;
(2)
(x+y)3
·
(x+y)4
.
1.计算:
解:
x
n
·
xn+1
=
解:
(x+y)3
·
(x+y)4
=
am
·
an
=
am+n
xn+(n+1)
=
x2n+1
公式中的a可代表一个数、字母、式子等.
(x+y)3+4
=(x+y)7
2.填空:
(1)
8
=
2x,则
x
=
;
(2)
8×
4
=
2x,则
x
=
;
(3)
3×27×9
=
3x,则
x
=
.
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
同底数幂相乘,
底数
指数
am
·
an
=
am+n
(m、n正整数)
小结
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子
公式
应用
不变,
相加.
再见!
