2020-2021学年苏科版七年级数学上册 2.5-2.6 有理数的加减乘除专题培优训练卷(word 版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学上册 2.5-2.6 有理数的加减乘除专题培优训练卷(word 版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 619.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 15:48:39 | ||
图片预览

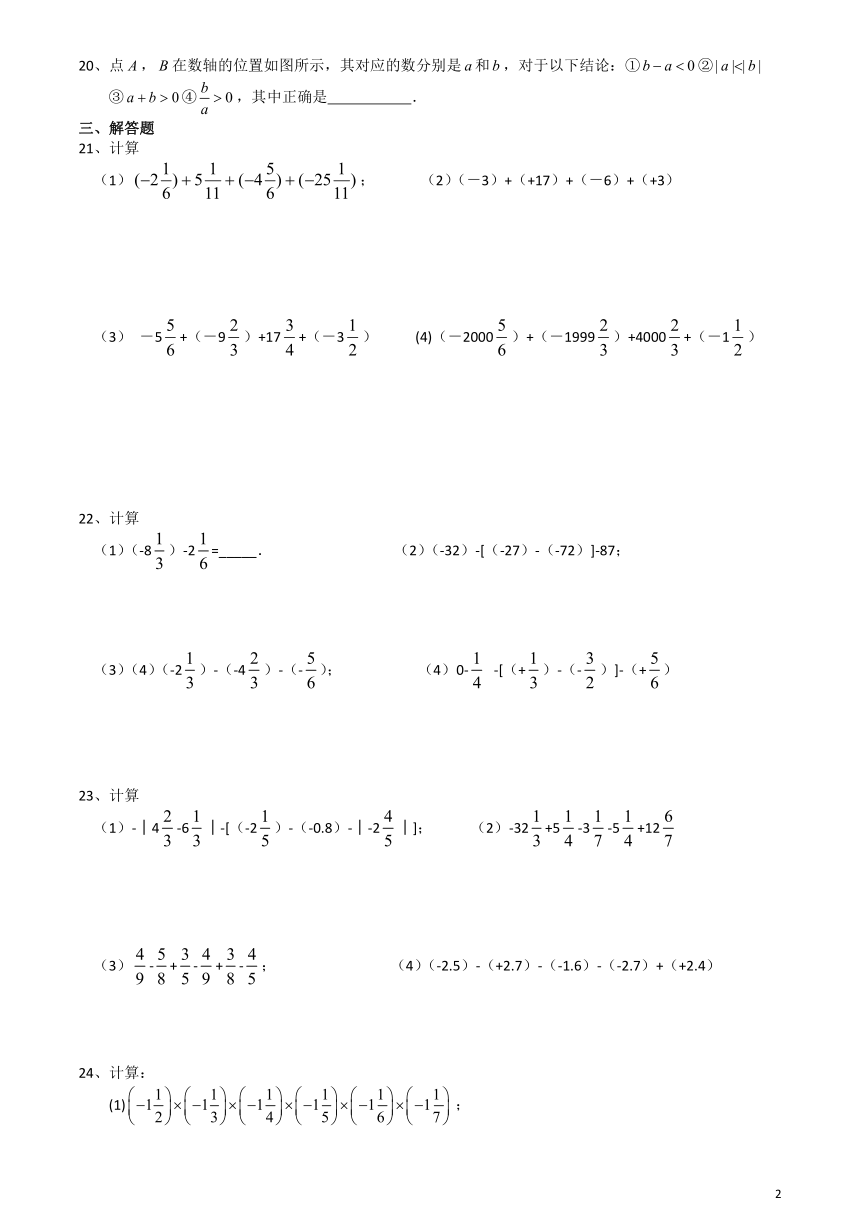


文档简介
2020-2021苏科版七年级数学上册第2章有理数2.5-2.6
有理数的加减乘除专题培优训练卷
一、选择题
1、下列说法正确的有( )
A.﹣a一定是负数
B.两个数的和一定大于每一个加数
C.绝对值等于本身的数是正数
D.最大的负整数是﹣1
2、若a<0,b>0,则a、a+b、a-b、b中最大的是
(
)
A.a
B.a+b
C.a-b
D.b
3、等于
(
)
A.
B.-
C.
D.-
4、下列运算中正确的是
(
)
A.3.58-(-1.58)=3.58+(-1.58)=2
B.(-2.6)-(-4)=2.6+4=6.6
C.
D.
5、已知|a|=6,|b|=2,且a>0,b<0,则a+b的值为( )
A.8
B.﹣8
C.4
D.﹣4
6、写成省略加号和的形式后为﹣6﹣7﹣2+9的式子是( )
A.(﹣6)﹣(+7)﹣(﹣2)+(+9)
B.﹣(+6)﹣(﹣7)﹣(+2)﹣(+9)
C.(﹣6)+(﹣7)+(+2)﹣(﹣9)
D.﹣6﹣(+7)+(﹣2)﹣(﹣9)
7、下列说法中正确的是
(
)
A.同号两数相乘,符号不变
B.异号两数相乘,取绝对值较大的因数的符号
C.两数相乘,积为正数,那么这两个数都为正数
D.两数相乘,积为负数,那么这两个数异号
8、利用分配律计算时,正确的方法可以是(
)
A.-
B.-
C.
D.
9、下列说法错误的是
(
)
A.任何有理数都有倒数
B.互为倒数的两个数的积为1
C.互为倒数的两个数同号
D.1和-1互为负倒数
10、如图所示,,是有理数,则式子化简的结果为
A.
B.
C.
D.
11、、、是有理数且,则的值是
A.
B.3或
C.或1
D.或
二、填空题
12、已知│3x-1│+(2y+3)=0,那么x-y=_______;
13、如果|a|=3,|b|=1,且a、b异号,则|a-b|=
.
14、已知有理数a,b,c在数轴上的对应位置如图所示,
则│c-1│+│a-c│+│a-b│化简后的结果是_______.
15、若|x|=9,|y|=6,且|x﹣y|=y﹣x,则x+y=
.
16、如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;
②a(b+c)>0;③a﹣c=b;④
.其中正确的是
17、规定一种新的运算:a△b=a×b-a-b+1.如,3△4=3×4-3-4+1=6.
(1)计算:-5△6=________;
(2)比较大小:(-3)△4_______4△(-3).
18、若a、b互为相反数,c、d互为倒数,m的绝对值是1,则(a+b)cd-2012m=__________
19、若,,则
20、点,在数轴的位置如图所示,其对应的数分别是和,对于以下结论:①②
③④,其中正确是
.
三、解答题
21、计算
(1);
(2)(-3)+(+17)+(-6)+(+3)
(3)
-5+(-9)+17+(-3)
(4)(-2000)+(-1999)+4000+(-1)
22、计算
(1)(-8)-2=_____.
(2)(-32)-[(-27)-(-72)]-87;
(3)(4)(-2)-(-4)-(-);
(4)0-
-[(+)-(-)]-(+)
23、计算
(1)-│4-6│-[(-2)-(-0.8)-│-2│];
(2)-32+5-3-5+12
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
24、计算:
(1);
(2);
(3);
(4);
(5).
25、计算
(1);
(2);
(3);
(4);
(5)
26、计算:
(1)
(2)
(3)
(4)
27、计算:.
28、在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x-y)+y的值.
29、已知、为有理数,现规定一种新运算,满足.
(1)_________;
(2)求的值.
(3)新运算是否满足加法交换律,若满足请说明理由:若不满足,请举出一个反例.
30、探索性问题:已知点A、B在数轴上分别表示m、n.
(1)填写下表:
m
5
﹣5
﹣6
﹣6
﹣10
n
3
0
4
﹣4
2
A、B两点的距离
2
(2)若A、B两点的距离为d,则d与m、n有何数量关系;
(3)在数轴上标出所有符合条件的整数点P,使它到3和﹣3的距离之和为6,并求出所有这些整数的和;
(4)若点C表示的数为x,当C在什么位置时,|x+2|+|x﹣3|取得值最小?
2020-2021苏科版七年级数学上册第2章有理数2.5-2.6
有理数的加减乘除专题培优训练卷
答案
一、选择题
1、下列说法正确的有( D )
A.﹣a一定是负数
B.两个数的和一定大于每一个加数
C.绝对值等于本身的数是正数
D.最大的负整数是﹣1
2、若a<0,b>0,则a、a+b、a-b、b中最大的是
(
D
)
A.a
B.a+b
C.a-b
D.b
3、等于
(
D
)
A.
B.-
C.
D.-
4、下列运算中正确的是
(
D
)
A.3.58-(-1.58)=3.58+(-1.58)=2
B.(-2.6)-(-4)=2.6+4=6.6
C.
D.
5、已知|a|=6,|b|=2,且a>0,b<0,则a+b的值为( C )
A.8
B.﹣8
C.4
D.﹣4
6、写成省略加号和的形式后为﹣6﹣7﹣2+9的式子是( D )
A.(﹣6)﹣(+7)﹣(﹣2)+(+9)
B.﹣(+6)﹣(﹣7)﹣(+2)﹣(+9)
C.(﹣6)+(﹣7)+(+2)﹣(﹣9)
D.﹣6﹣(+7)+(﹣2)﹣(﹣9)
7、下列说法中正确的是
(
D
)
A.同号两数相乘,符号不变
B.异号两数相乘,取绝对值较大的因数的符号
C.两数相乘,积为正数,那么这两个数都为正数
D.两数相乘,积为负数,那么这两个数异号
8、利用分配律计算时,正确的方法可以是(
A
)
A.-
B.-
C.
D.
9、下列说法错误的是
(
A
)
A.任何有理数都有倒数
B.互为倒数的两个数的积为1
C.互为倒数的两个数同号
D.1和-1互为负倒数
10、如图所示,,是有理数,则式子化简的结果为 D
A.
B.
C.
D.
11、、、是有理数且,则的值是 C
A.
B.3或
C.或1
D.或
二、填空题
12、已知│3x-1│+(2y+3)=0,那么x-y=_______;
13、如果|a|=3,|b|=1,且a、b异号,则|a-b|=
4或-4
.
14、已知有理数a,b,c在数轴上的对应位置如图所示,
则│c-1│+│a-c│+│a-b│化简后的结果是___1-2c+b____.
15、若|x|=9,|y|=6,且|x﹣y|=y﹣x,则x+y= ﹣3或﹣15 .
16、如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;
②a(b+c)>0;③a﹣c=b;④
.其中正确的是②、③
17、规定一种新的运算:a△b=a×b-a-b+1.如,3△4=3×4-3-4+1=6.
(1)计算:-5△6=____-30____;
(2)比较大小:(-3)△4___=____4△(-3).
18、若a、b互为相反数,c、d互为倒数,m的绝对值是1,则(a+b)cd-2012m=__________
答案:±2012
19、若,,则 或
20、点,在数轴的位置如图所示,其对应的数分别是和,对于以下结论:①②
③④,其中正确是 ②③ .
三、解答题
21、计算
(1);
(2)(-3)+(+17)+(-6)+(+3)
(3)
-5+(-9)+17+(-3)
(4)(-2000)+(-1999)+4000+(-1)
(1)-27
;
(2)11
(3)解:原式=[(-5)+(-)]+[(-9)+(-)]+(17+)+[(-3)+(-)]
=[(-5)+(-9)+17+(-13)]+[
(-)+(-)++(-)]
=0+(-1)=-1…………这种解题方法叫做拆项法.
(4)
22、计算
(1)(-8)-2=_____.
(2)(-32)-[(-27)-(-72)]-87;
(3)(4)(-2)-(-4)-(-);
(4)0-
-[(+)-(-)]-(+)
(1)-;
(2)-164;
(3)3;(4)-
23、计算
(1)-│4-6│-[(-2)-(-0.8)-│-2│];
(2)-32+5-3-5+12
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
(1)2;(2)-22
(3)-;(4)1.5
24、计算:
(1);
(2);
(3);
(4);
(5).
(1)
(2)
(3)- (4)
(5)-13.34
25、计算
(1);
(2);
(3);
(4);
(5)
(1)
(2)1
(3)47 (4)-1
(5)9
26、计算:
(1)
(2)
(3)
(4)
(1)-7
(2)
(3)
(4)-22
27、计算:.
()
28、在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x-y)+y的值.
解:(1)共有以下几种情况:(-5)×1×(-3)=15,(-5)×1×5=-25,-5×1×(-2)=10,-5×(-3)×5=75,-5×(-3)×(-2)=-30,-5×5×(-2)=50,1×(-3)×5=-15,1×(-3)×(-2)=6,(-3)×5×(-2)=30,1×5×(-2)=-10,
最大的积是a=75,最小的积是b=-30.
(2)由|x+75|+|y+30|=0,得x+75=0,
y+30=0,则x=-75,y=-30,
所以(x-y)+y=(-75+30)+(-30)=-75.
29、已知、为有理数,现规定一种新运算,满足.
(1)_________;
(2)求的值.
(3)新运算是否满足加法交换律,若满足请说明理由:若不满足,请举出一个反例.
(1)-6;(2);(3)不满足,举例见略
30、探索性问题:已知点A、B在数轴上分别表示m、n.
(1)填写下表:
m
5
﹣5
﹣6
﹣6
﹣10
n
3
0
4
﹣4
2
A、B两点的距离
2
(2)若A、B两点的距离为d,则d与m、n有何数量关系;
(3)在数轴上标出所有符合条件的整数点P,使它到3和﹣3的距离之和为6,并求出所有这些整数的和;
(4)若点C表示的数为x,当C在什么位置时,|x+2|+|x﹣3|取得值最小?
【分析】(1)观察数轴,得出A、B两点的距离;
【解析】(1)见表格;
m
5
﹣5
﹣6
﹣6
﹣10
n
3
0
4
﹣4
2
A、B两点的距离
2
5
10
2
12
(2)d=|m﹣n|;
(3)符合条件的整数点P有7个,如图;
所有这些整数和为:﹣3﹣2﹣1+0+1+2+3=0.
(4)|x+2|表示点C到点﹣2的距离,|x﹣3|表示点C到点3的距离,
当点C在点﹣2和点3之间时,|x+2|+|x﹣3|的值最小,
此时﹣2≤x≤3.
有理数的加减乘除专题培优训练卷
一、选择题
1、下列说法正确的有( )
A.﹣a一定是负数
B.两个数的和一定大于每一个加数
C.绝对值等于本身的数是正数
D.最大的负整数是﹣1
2、若a<0,b>0,则a、a+b、a-b、b中最大的是
(
)
A.a
B.a+b
C.a-b
D.b
3、等于
(
)
A.
B.-
C.
D.-
4、下列运算中正确的是
(
)
A.3.58-(-1.58)=3.58+(-1.58)=2
B.(-2.6)-(-4)=2.6+4=6.6
C.
D.
5、已知|a|=6,|b|=2,且a>0,b<0,则a+b的值为( )
A.8
B.﹣8
C.4
D.﹣4
6、写成省略加号和的形式后为﹣6﹣7﹣2+9的式子是( )
A.(﹣6)﹣(+7)﹣(﹣2)+(+9)
B.﹣(+6)﹣(﹣7)﹣(+2)﹣(+9)
C.(﹣6)+(﹣7)+(+2)﹣(﹣9)
D.﹣6﹣(+7)+(﹣2)﹣(﹣9)
7、下列说法中正确的是
(
)
A.同号两数相乘,符号不变
B.异号两数相乘,取绝对值较大的因数的符号
C.两数相乘,积为正数,那么这两个数都为正数
D.两数相乘,积为负数,那么这两个数异号
8、利用分配律计算时,正确的方法可以是(
)
A.-
B.-
C.
D.
9、下列说法错误的是
(
)
A.任何有理数都有倒数
B.互为倒数的两个数的积为1
C.互为倒数的两个数同号
D.1和-1互为负倒数
10、如图所示,,是有理数,则式子化简的结果为
A.
B.
C.
D.
11、、、是有理数且,则的值是
A.
B.3或
C.或1
D.或
二、填空题
12、已知│3x-1│+(2y+3)=0,那么x-y=_______;
13、如果|a|=3,|b|=1,且a、b异号,则|a-b|=
.
14、已知有理数a,b,c在数轴上的对应位置如图所示,
则│c-1│+│a-c│+│a-b│化简后的结果是_______.
15、若|x|=9,|y|=6,且|x﹣y|=y﹣x,则x+y=
.
16、如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;
②a(b+c)>0;③a﹣c=b;④
.其中正确的是
17、规定一种新的运算:a△b=a×b-a-b+1.如,3△4=3×4-3-4+1=6.
(1)计算:-5△6=________;
(2)比较大小:(-3)△4_______4△(-3).
18、若a、b互为相反数,c、d互为倒数,m的绝对值是1,则(a+b)cd-2012m=__________
19、若,,则
20、点,在数轴的位置如图所示,其对应的数分别是和,对于以下结论:①②
③④,其中正确是
.
三、解答题
21、计算
(1);
(2)(-3)+(+17)+(-6)+(+3)
(3)
-5+(-9)+17+(-3)
(4)(-2000)+(-1999)+4000+(-1)
22、计算
(1)(-8)-2=_____.
(2)(-32)-[(-27)-(-72)]-87;
(3)(4)(-2)-(-4)-(-);
(4)0-
-[(+)-(-)]-(+)
23、计算
(1)-│4-6│-[(-2)-(-0.8)-│-2│];
(2)-32+5-3-5+12
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
24、计算:
(1);
(2);
(3);
(4);
(5).
25、计算
(1);
(2);
(3);
(4);
(5)
26、计算:
(1)
(2)
(3)
(4)
27、计算:.
28、在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x-y)+y的值.
29、已知、为有理数,现规定一种新运算,满足.
(1)_________;
(2)求的值.
(3)新运算是否满足加法交换律,若满足请说明理由:若不满足,请举出一个反例.
30、探索性问题:已知点A、B在数轴上分别表示m、n.
(1)填写下表:
m
5
﹣5
﹣6
﹣6
﹣10
n
3
0
4
﹣4
2
A、B两点的距离
2
(2)若A、B两点的距离为d,则d与m、n有何数量关系;
(3)在数轴上标出所有符合条件的整数点P,使它到3和﹣3的距离之和为6,并求出所有这些整数的和;
(4)若点C表示的数为x,当C在什么位置时,|x+2|+|x﹣3|取得值最小?
2020-2021苏科版七年级数学上册第2章有理数2.5-2.6
有理数的加减乘除专题培优训练卷
答案
一、选择题
1、下列说法正确的有( D )
A.﹣a一定是负数
B.两个数的和一定大于每一个加数
C.绝对值等于本身的数是正数
D.最大的负整数是﹣1
2、若a<0,b>0,则a、a+b、a-b、b中最大的是
(
D
)
A.a
B.a+b
C.a-b
D.b
3、等于
(
D
)
A.
B.-
C.
D.-
4、下列运算中正确的是
(
D
)
A.3.58-(-1.58)=3.58+(-1.58)=2
B.(-2.6)-(-4)=2.6+4=6.6
C.
D.
5、已知|a|=6,|b|=2,且a>0,b<0,则a+b的值为( C )
A.8
B.﹣8
C.4
D.﹣4
6、写成省略加号和的形式后为﹣6﹣7﹣2+9的式子是( D )
A.(﹣6)﹣(+7)﹣(﹣2)+(+9)
B.﹣(+6)﹣(﹣7)﹣(+2)﹣(+9)
C.(﹣6)+(﹣7)+(+2)﹣(﹣9)
D.﹣6﹣(+7)+(﹣2)﹣(﹣9)
7、下列说法中正确的是
(
D
)
A.同号两数相乘,符号不变
B.异号两数相乘,取绝对值较大的因数的符号
C.两数相乘,积为正数,那么这两个数都为正数
D.两数相乘,积为负数,那么这两个数异号
8、利用分配律计算时,正确的方法可以是(
A
)
A.-
B.-
C.
D.
9、下列说法错误的是
(
A
)
A.任何有理数都有倒数
B.互为倒数的两个数的积为1
C.互为倒数的两个数同号
D.1和-1互为负倒数
10、如图所示,,是有理数,则式子化简的结果为 D
A.
B.
C.
D.
11、、、是有理数且,则的值是 C
A.
B.3或
C.或1
D.或
二、填空题
12、已知│3x-1│+(2y+3)=0,那么x-y=_______;
13、如果|a|=3,|b|=1,且a、b异号,则|a-b|=
4或-4
.
14、已知有理数a,b,c在数轴上的对应位置如图所示,
则│c-1│+│a-c│+│a-b│化简后的结果是___1-2c+b____.
15、若|x|=9,|y|=6,且|x﹣y|=y﹣x,则x+y= ﹣3或﹣15 .
16、如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:①abc<0;
②a(b+c)>0;③a﹣c=b;④
.其中正确的是②、③
17、规定一种新的运算:a△b=a×b-a-b+1.如,3△4=3×4-3-4+1=6.
(1)计算:-5△6=____-30____;
(2)比较大小:(-3)△4___=____4△(-3).
18、若a、b互为相反数,c、d互为倒数,m的绝对值是1,则(a+b)cd-2012m=__________
答案:±2012
19、若,,则 或
20、点,在数轴的位置如图所示,其对应的数分别是和,对于以下结论:①②
③④,其中正确是 ②③ .
三、解答题
21、计算
(1);
(2)(-3)+(+17)+(-6)+(+3)
(3)
-5+(-9)+17+(-3)
(4)(-2000)+(-1999)+4000+(-1)
(1)-27
;
(2)11
(3)解:原式=[(-5)+(-)]+[(-9)+(-)]+(17+)+[(-3)+(-)]
=[(-5)+(-9)+17+(-13)]+[
(-)+(-)++(-)]
=0+(-1)=-1…………这种解题方法叫做拆项法.
(4)
22、计算
(1)(-8)-2=_____.
(2)(-32)-[(-27)-(-72)]-87;
(3)(4)(-2)-(-4)-(-);
(4)0-
-[(+)-(-)]-(+)
(1)-;
(2)-164;
(3)3;(4)-
23、计算
(1)-│4-6│-[(-2)-(-0.8)-│-2│];
(2)-32+5-3-5+12
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
(1)2;(2)-22
(3)-;(4)1.5
24、计算:
(1);
(2);
(3);
(4);
(5).
(1)
(2)
(3)- (4)
(5)-13.34
25、计算
(1);
(2);
(3);
(4);
(5)
(1)
(2)1
(3)47 (4)-1
(5)9
26、计算:
(1)
(2)
(3)
(4)
(1)-7
(2)
(3)
(4)-22
27、计算:.
()
28、在数-5,1,-3,5,-2中任取三个数相乘,其中最大的积是a,最小的积是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x-y)+y的值.
解:(1)共有以下几种情况:(-5)×1×(-3)=15,(-5)×1×5=-25,-5×1×(-2)=10,-5×(-3)×5=75,-5×(-3)×(-2)=-30,-5×5×(-2)=50,1×(-3)×5=-15,1×(-3)×(-2)=6,(-3)×5×(-2)=30,1×5×(-2)=-10,
最大的积是a=75,最小的积是b=-30.
(2)由|x+75|+|y+30|=0,得x+75=0,
y+30=0,则x=-75,y=-30,
所以(x-y)+y=(-75+30)+(-30)=-75.
29、已知、为有理数,现规定一种新运算,满足.
(1)_________;
(2)求的值.
(3)新运算是否满足加法交换律,若满足请说明理由:若不满足,请举出一个反例.
(1)-6;(2);(3)不满足,举例见略
30、探索性问题:已知点A、B在数轴上分别表示m、n.
(1)填写下表:
m
5
﹣5
﹣6
﹣6
﹣10
n
3
0
4
﹣4
2
A、B两点的距离
2
(2)若A、B两点的距离为d,则d与m、n有何数量关系;
(3)在数轴上标出所有符合条件的整数点P,使它到3和﹣3的距离之和为6,并求出所有这些整数的和;
(4)若点C表示的数为x,当C在什么位置时,|x+2|+|x﹣3|取得值最小?
【分析】(1)观察数轴,得出A、B两点的距离;
【解析】(1)见表格;
m
5
﹣5
﹣6
﹣6
﹣10
n
3
0
4
﹣4
2
A、B两点的距离
2
5
10
2
12
(2)d=|m﹣n|;
(3)符合条件的整数点P有7个,如图;
所有这些整数和为:﹣3﹣2﹣1+0+1+2+3=0.
(4)|x+2|表示点C到点﹣2的距离,|x﹣3|表示点C到点3的距离,
当点C在点﹣2和点3之间时,|x+2|+|x﹣3|的值最小,
此时﹣2≤x≤3.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
