人教版九年级上册22.2二次函数与一元二次方程课件(21张)
文档属性
| 名称 | 人教版九年级上册22.2二次函数与一元二次方程课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 787.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 18:14:36 | ||
图片预览







文档简介
(共22张PPT)
第二十二章
二次函数
二次函数与一元二次方程
学习目标
1.通过探索,理解二次函数与一元二次方程(不等式)之间的联系.(难点)
2.能运用二次函数及其图象、性质确定方程的解或不等式的解集.(重点)
3.了解用图象法求一元二次方程的近似根.
导入新课
情境引入
问题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:
h=20t-5t2,
考虑以下问题:
复习
1、
一元二次方程的一般形式是什么?
2、如何判断一元二次方程的根的情况?
3、函数y=x2-3x+2的图像与x轴有交点吗?如果有,交点坐标是什么?
自学指导
阅读教材p43-45思考下列问题:
1、问题1中,小球飞行最高是多少米?最低是多少米?你怎样理解?
2、解下列方程并对照课本45页(图22.2-2)观察函数图像与x轴交点坐标与对应的一元二次方程的解有什么关系?
(1)x2+x-2=0
(2)x2-6x+9=0
(3)x2-x+1=0
3、二次函数y=ax2+bx+c的图像与x轴的位置关系有几种?与对应的一元二次方程ax2+bx+c=0根的情况有什么联系?
问题1:如图,以
40
m
/s的速度将小球沿与地面成
30度角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度
h
(单位:m)与飞行时间
t
(单位:s)之间具有关系:
h=
20
t
–
5
t2
考虑下列问题:
(1)球的飞行高度能否达到
15
m?
若能,需要多少时间?
(2)球的飞行高度能否达到
20
m?
若能,需要多少时间?
(3)球的飞行高度能否达到
20.5
m?
若能,需要多少时间?
(4)球从飞出到落地要用多少时间?
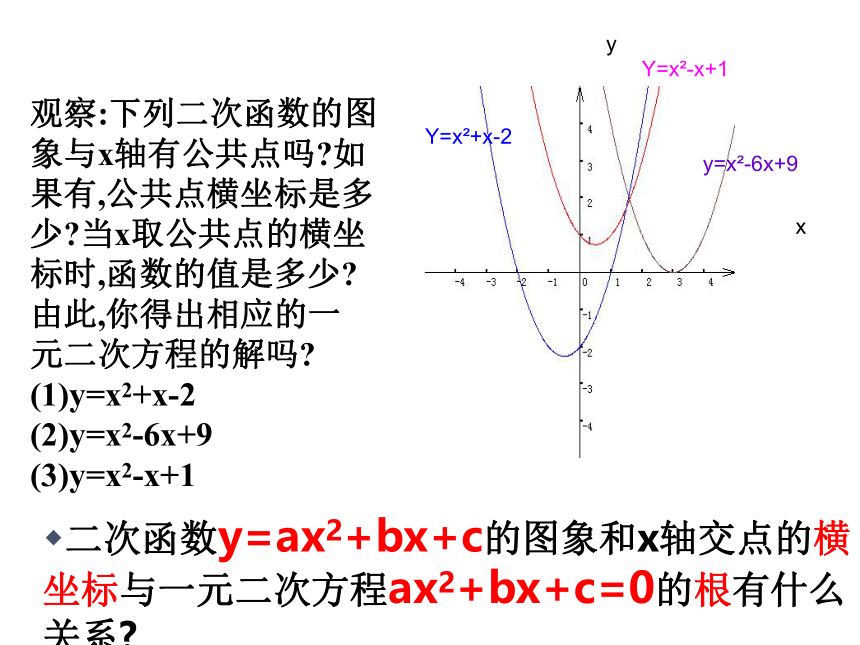
观察:下列二次函数的图
象与x轴有公共点吗?如
果有,公共点横坐标是多
少?当x取公共点的横坐
标时,函数的值是多少?
由此,你得出相应的一
元二次方程的解吗?
(1)y=x2+x-2
(2)y=x2-6x+9
(3)y=x2-x+1
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
y=x?-6x+9
Y=x?+x-2
Y=x?-x+1
x
y
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac
>
0
只有一个交点
有两个相等的实数根
b2-4ac
=
0
没有交点
没有实数根
b2-4ac
<
0
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
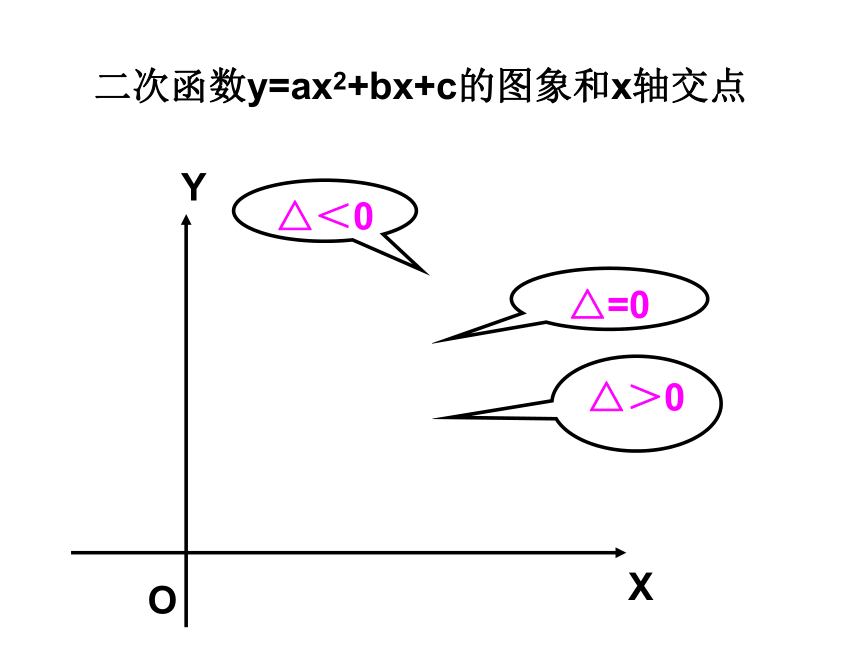
归纳:
△>0
△=0
△<0
O
X
Y
二次函数y=ax2+bx+c的图象和x轴交点
课堂练习
1.不与x轴相交的抛物线是(
)
A
y=2x2
–
3
B
y=
-
2
x2
+
3
C
y=
-
x2
–
3x
D
y=-2(x+1)2
-
3
2.若抛物线y=ax2+bx+c,当
a>0,c<0时,图象与x轴交点情况是(
)
A
无交点
B
只有一个交点
C
有两个交点
D不能确定
D
C
3.如果关于x的一元二次方程
x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线
y=x2-2x+m与x轴有_个交点.
4.已知抛物线
y=x2
–
8x
+c的顶点在
x轴上,则c=____.
1
1
16
5、下列二次函数的图象与
x
轴有交点吗?
若有,求出交点坐标.
(1)
y
=
2x2+x-3
(2)
y
=
4x2
-
4x
+1
(3)
y
=
x2
–
x+
1
当堂检测
1.抛物线y=2x2-3x-5
与y轴交于点____,与x轴交于点 .
2.一元二次方程
3
x2+x-10=0的两个根是x1=
-2
,x2=5/3,
那么二次函数y=
3
x2+x-10与x轴的交点坐标是_____.
归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2
,则抛物线
y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)
(0,-5)
(5/2,0)
(-1,0)
(-2,0)
(5/3,0)
3.如图,抛物线y=ax2+bx+c的对称轴是直线
x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3
,x2=___
-3.3
x
A
o
y
X=-1
3
-1
1.3
.
4、已知抛物线y=x2
+
mx
+m
–
2
求证:
无论
m取何值,抛物线总与x轴有两个交点.
冲击中考:
1.若抛物线
y=x2
+
bx+
c
的顶点在第一象限,则方程
x2
+
bx+
c
=0
的根的情况是_____.
2.直线
y=2x+1
与抛物线
y=
x2
+
4x
+3
有____个交点.
课后练习
A
组
1.
抛物线y=x2-3x+5与坐标轴的交点个数为
(
)
A.
无交点
B.
1个
C.
2个
D.
3个
B
2.
已知二次函数y=3x2+c的图象与x轴只有一个交点,
则c的值为
(
)
A.
B.
C.
3
D.
0
D
3.
关于x的二次函数y=x2+4x+m的图象与x轴有交点,则m的取值范围是____________.
4.
二次函数y=x2+2kx+k2的图象与x轴的一个交点的坐标为(-2,0),则k的值是____________.
m≤4
2
5.
某抛物线与x轴的交点坐标分别为(-1,0)和(3,0),则该抛物线的对称轴为直线x=________.
1
6.
已知二次函数y=x2+px+q的图象与x轴只有一个公共点,点的坐标为(-1,0),求p,q的值.
解:根据题意,得
解得
B
组
7.
已知二次函数y=x2-x-6与x轴交于A,B两点,则线段AB的值为
(
)
A.
5
B.
2
C.
3
D.
1
A
8.
二次函数y=mx2-6x+2的图象与x轴只有一个公共点,求m的值.
解:∵二次函数y=mx2-6x+2的图象与x轴只有一个公共点,
∴Δ=(-6)2-4×2m=0.
解得m=
故m的值是
C
组
9.
已知抛物线y=x2-3x-4与x轴相交于A,B两点,与y轴相交于点C,求△ABC的面积.
解:由y=x2-3x-4,当y=0时,x2-3x-4=0.
解得x1=4,x2=-1.
∴抛物线与x轴的交点坐标是(-1,0),
(4,0).
当x=0时,y=-4.
∴抛物线与y轴的交点坐标为C(0,-4).
∴△ABC的面积为
×[4-(-1)]×4=10.
第二十二章
二次函数
二次函数与一元二次方程
学习目标
1.通过探索,理解二次函数与一元二次方程(不等式)之间的联系.(难点)
2.能运用二次函数及其图象、性质确定方程的解或不等式的解集.(重点)
3.了解用图象法求一元二次方程的近似根.
导入新课
情境引入
问题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:
h=20t-5t2,
考虑以下问题:
复习
1、
一元二次方程的一般形式是什么?
2、如何判断一元二次方程的根的情况?
3、函数y=x2-3x+2的图像与x轴有交点吗?如果有,交点坐标是什么?
自学指导
阅读教材p43-45思考下列问题:
1、问题1中,小球飞行最高是多少米?最低是多少米?你怎样理解?
2、解下列方程并对照课本45页(图22.2-2)观察函数图像与x轴交点坐标与对应的一元二次方程的解有什么关系?
(1)x2+x-2=0
(2)x2-6x+9=0
(3)x2-x+1=0
3、二次函数y=ax2+bx+c的图像与x轴的位置关系有几种?与对应的一元二次方程ax2+bx+c=0根的情况有什么联系?
问题1:如图,以
40
m
/s的速度将小球沿与地面成
30度角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度
h
(单位:m)与飞行时间
t
(单位:s)之间具有关系:
h=
20
t
–
5
t2
考虑下列问题:
(1)球的飞行高度能否达到
15
m?
若能,需要多少时间?
(2)球的飞行高度能否达到
20
m?
若能,需要多少时间?
(3)球的飞行高度能否达到
20.5
m?
若能,需要多少时间?
(4)球从飞出到落地要用多少时间?
观察:下列二次函数的图
象与x轴有公共点吗?如
果有,公共点横坐标是多
少?当x取公共点的横坐
标时,函数的值是多少?
由此,你得出相应的一
元二次方程的解吗?
(1)y=x2+x-2
(2)y=x2-6x+9
(3)y=x2-x+1
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
y=x?-6x+9
Y=x?+x-2
Y=x?-x+1
x
y
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac
>
0
只有一个交点
有两个相等的实数根
b2-4ac
=
0
没有交点
没有实数根
b2-4ac
<
0
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
归纳:
△>0
△=0
△<0
O
X
Y
二次函数y=ax2+bx+c的图象和x轴交点
课堂练习
1.不与x轴相交的抛物线是(
)
A
y=2x2
–
3
B
y=
-
2
x2
+
3
C
y=
-
x2
–
3x
D
y=-2(x+1)2
-
3
2.若抛物线y=ax2+bx+c,当
a>0,c<0时,图象与x轴交点情况是(
)
A
无交点
B
只有一个交点
C
有两个交点
D不能确定
D
C
3.如果关于x的一元二次方程
x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线
y=x2-2x+m与x轴有_个交点.
4.已知抛物线
y=x2
–
8x
+c的顶点在
x轴上,则c=____.
1
1
16
5、下列二次函数的图象与
x
轴有交点吗?
若有,求出交点坐标.
(1)
y
=
2x2+x-3
(2)
y
=
4x2
-
4x
+1
(3)
y
=
x2
–
x+
1
当堂检测
1.抛物线y=2x2-3x-5
与y轴交于点____,与x轴交于点 .
2.一元二次方程
3
x2+x-10=0的两个根是x1=
-2
,x2=5/3,
那么二次函数y=
3
x2+x-10与x轴的交点坐标是_____.
归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2
,则抛物线
y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)
(0,-5)
(5/2,0)
(-1,0)
(-2,0)
(5/3,0)
3.如图,抛物线y=ax2+bx+c的对称轴是直线
x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3
,x2=___
-3.3
x
A
o
y
X=-1
3
-1
1.3
.
4、已知抛物线y=x2
+
mx
+m
–
2
求证:
无论
m取何值,抛物线总与x轴有两个交点.
冲击中考:
1.若抛物线
y=x2
+
bx+
c
的顶点在第一象限,则方程
x2
+
bx+
c
=0
的根的情况是_____.
2.直线
y=2x+1
与抛物线
y=
x2
+
4x
+3
有____个交点.
课后练习
A
组
1.
抛物线y=x2-3x+5与坐标轴的交点个数为
(
)
A.
无交点
B.
1个
C.
2个
D.
3个
B
2.
已知二次函数y=3x2+c的图象与x轴只有一个交点,
则c的值为
(
)
A.
B.
C.
3
D.
0
D
3.
关于x的二次函数y=x2+4x+m的图象与x轴有交点,则m的取值范围是____________.
4.
二次函数y=x2+2kx+k2的图象与x轴的一个交点的坐标为(-2,0),则k的值是____________.
m≤4
2
5.
某抛物线与x轴的交点坐标分别为(-1,0)和(3,0),则该抛物线的对称轴为直线x=________.
1
6.
已知二次函数y=x2+px+q的图象与x轴只有一个公共点,点的坐标为(-1,0),求p,q的值.
解:根据题意,得
解得
B
组
7.
已知二次函数y=x2-x-6与x轴交于A,B两点,则线段AB的值为
(
)
A.
5
B.
2
C.
3
D.
1
A
8.
二次函数y=mx2-6x+2的图象与x轴只有一个公共点,求m的值.
解:∵二次函数y=mx2-6x+2的图象与x轴只有一个公共点,
∴Δ=(-6)2-4×2m=0.
解得m=
故m的值是
C
组
9.
已知抛物线y=x2-3x-4与x轴相交于A,B两点,与y轴相交于点C,求△ABC的面积.
解:由y=x2-3x-4,当y=0时,x2-3x-4=0.
解得x1=4,x2=-1.
∴抛物线与x轴的交点坐标是(-1,0),
(4,0).
当x=0时,y=-4.
∴抛物线与y轴的交点坐标为C(0,-4).
∴△ABC的面积为
×[4-(-1)]×4=10.
同课章节目录
