人教版数学八年级上册11.2.2三角形的外角和教案
文档属性
| 名称 | 人教版数学八年级上册11.2.2三角形的外角和教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 10:30:36 | ||
图片预览

文档简介
11.2.2三角形的外角
1、
理解三角形的外角的概念
2、
掌握三角形的外角的两个性质,能利用三角形的外角性质解决实际问题.
三角形外角的性质,外角和定理.
三角形外角的定义及定理的推理过程.
教学过程
一、创设情景,明确目标
1、在△ABC
中,∠A
=75°,∠B
=40°,
∠C
等于多少度?
2、如图,△ABC中,CD是BC边的延长线,
∠A=60°,∠B=55°.
(1)求∠ACD的度数.(115°)
(2)∠ACD与∠A,∠B有什么大小关系?
(∠ACD=∠A+∠B)
二、新课探究
1、让学生阅读教材第14-15页内容。
2、让学生说一说阅读教材后的收获。
3、师生共同归纳有关概念
(1)三角形外角的概念:
思考
如图,把△ABC
的一边BC
延长,得到
∠ACD.这个角还是三角形的内角吗?
概念:三角形的一边与另一边的延长线组成的角,叫做三角形
的外角.
例如,把△ABC
的一边BC
延长,得到∠ACD,∠ACD是
△ABC的一个外角。
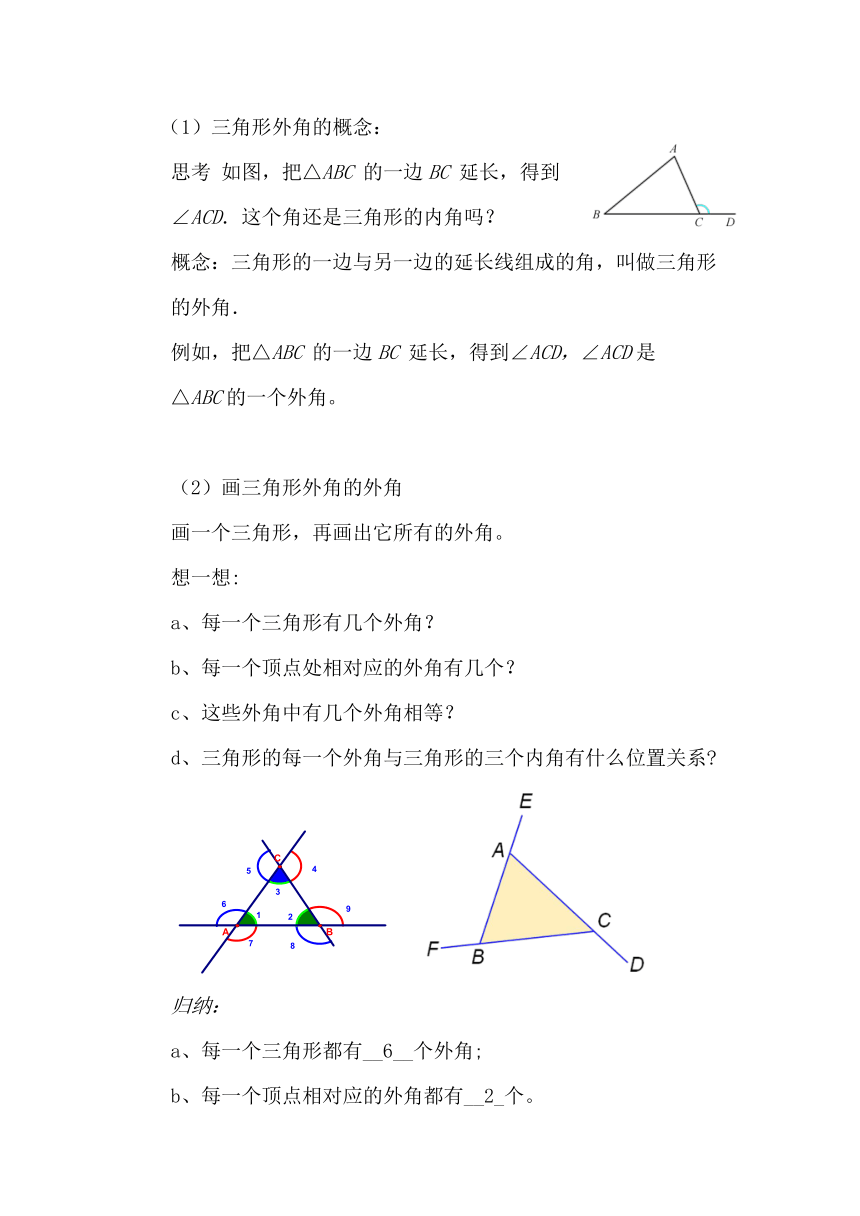
(2)画三角形外角的外角
画一个三角形,再画出它所有的外角。
想一想:
a、每一个三角形有几个外角?
b、每一个顶点处相对应的外角有几个?
c、这些外角中有几个外角相等?
d、三角形的每一个外角与三角形的三个内角有什么位置关系?
归纳:
a、每一个三角形都有__6__个外角;
b、每一个顶点相对应的外角都有__2_个。
c、这6个外角中有__3___对外角相等。
d、一个三角形的每一个外角对应一个
______相邻的内角_______和两个_不相邻的内角____.
4、三角形的外角的性质及外角和
(1)
三角形外角的性质:
三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的外角和等于360°
5、三角形外角结论的运用
教材P15 例4
6、总结梳理,内化目标
三角形外角的定义,三角形外角的性质.
7、达标检测,反思目标
1.判断题:
(1)三角形的外角和是指三角形所有外角的和.(×)
(2)三角形的外角和等于它内角和的2倍.(√)
(3)三角形的一个外角等于两个内角的和.(×)
(4)三角形的一个外角等于与它不相邻的两个内角的和.(√)
(5)三角形的一个外角大于任何一个内角.(×)
(6)三角形的一个内角小于任何一个与它不相邻的外角.(√)
2.填空:
(1)如图.
∠A+∠B+∠C+∠D+∠E+∠F=__360°__.
(2)五角星的五个角的和是__180°__.
3.如图,图甲中的∠1=69°,图乙中的∠2=21°.
4.如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角的平分线,交BC的延长线于点E,且∠BAD=20°,∠E=50°,求∠ACD的度数.
解:∵AD平分∠BAC,∠BAD=20°,∴∠BAC=2∠BAD=40°,
∴∠CAF=180°-∠BAC=140°,∵AE平分∠CAF,
∴∠CAE=∠CAF=70°,∴∠ACD=∠E+∠CAE=120°
作业布置
课本P17 5、6、7、11.
1、
理解三角形的外角的概念
2、
掌握三角形的外角的两个性质,能利用三角形的外角性质解决实际问题.
三角形外角的性质,外角和定理.
三角形外角的定义及定理的推理过程.
教学过程
一、创设情景,明确目标
1、在△ABC
中,∠A
=75°,∠B
=40°,
∠C
等于多少度?
2、如图,△ABC中,CD是BC边的延长线,
∠A=60°,∠B=55°.
(1)求∠ACD的度数.(115°)
(2)∠ACD与∠A,∠B有什么大小关系?
(∠ACD=∠A+∠B)
二、新课探究
1、让学生阅读教材第14-15页内容。
2、让学生说一说阅读教材后的收获。
3、师生共同归纳有关概念
(1)三角形外角的概念:
思考
如图,把△ABC
的一边BC
延长,得到
∠ACD.这个角还是三角形的内角吗?
概念:三角形的一边与另一边的延长线组成的角,叫做三角形
的外角.
例如,把△ABC
的一边BC
延长,得到∠ACD,∠ACD是
△ABC的一个外角。
(2)画三角形外角的外角
画一个三角形,再画出它所有的外角。
想一想:
a、每一个三角形有几个外角?
b、每一个顶点处相对应的外角有几个?
c、这些外角中有几个外角相等?
d、三角形的每一个外角与三角形的三个内角有什么位置关系?
归纳:
a、每一个三角形都有__6__个外角;
b、每一个顶点相对应的外角都有__2_个。
c、这6个外角中有__3___对外角相等。
d、一个三角形的每一个外角对应一个
______相邻的内角_______和两个_不相邻的内角____.
4、三角形的外角的性质及外角和
(1)
三角形外角的性质:
三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的外角和等于360°
5、三角形外角结论的运用
教材P15 例4
6、总结梳理,内化目标
三角形外角的定义,三角形外角的性质.
7、达标检测,反思目标
1.判断题:
(1)三角形的外角和是指三角形所有外角的和.(×)
(2)三角形的外角和等于它内角和的2倍.(√)
(3)三角形的一个外角等于两个内角的和.(×)
(4)三角形的一个外角等于与它不相邻的两个内角的和.(√)
(5)三角形的一个外角大于任何一个内角.(×)
(6)三角形的一个内角小于任何一个与它不相邻的外角.(√)
2.填空:
(1)如图.
∠A+∠B+∠C+∠D+∠E+∠F=__360°__.
(2)五角星的五个角的和是__180°__.
3.如图,图甲中的∠1=69°,图乙中的∠2=21°.
4.如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角的平分线,交BC的延长线于点E,且∠BAD=20°,∠E=50°,求∠ACD的度数.
解:∵AD平分∠BAC,∠BAD=20°,∴∠BAC=2∠BAD=40°,
∴∠CAF=180°-∠BAC=140°,∵AE平分∠CAF,
∴∠CAE=∠CAF=70°,∴∠ACD=∠E+∠CAE=120°
作业布置
课本P17 5、6、7、11.
