人教版数学七年级上册1.2.1 有理数 课件(17张)
文档属性
| 名称 | 人教版数学七年级上册1.2.1 有理数 课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 402.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 18:20:49 | ||
图片预览




文档简介
(共18张PPT)
1.2.1有理数
我们学过的数:
正整数,如:1、2、3……
零,0
负整数,如:-1、-2、-3
……
正分数,如:
、
、
、0.1、5.32……
负分数,如:
、
、
-0.5、
-150.32……
整
数
分
数
正整数、零、负整数统称为整数。
正分数、负分数统称为分数。
整数和分数统称为有理数。
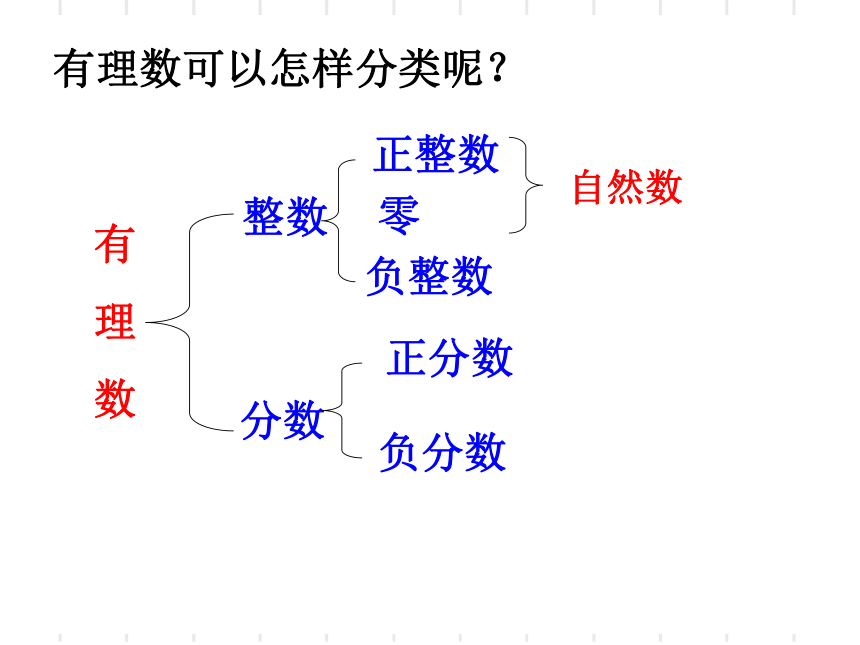
有理数可以怎样分类呢?
有
理
数
整数
分数
正整数
零
负整数
正分数
负分数
自然数
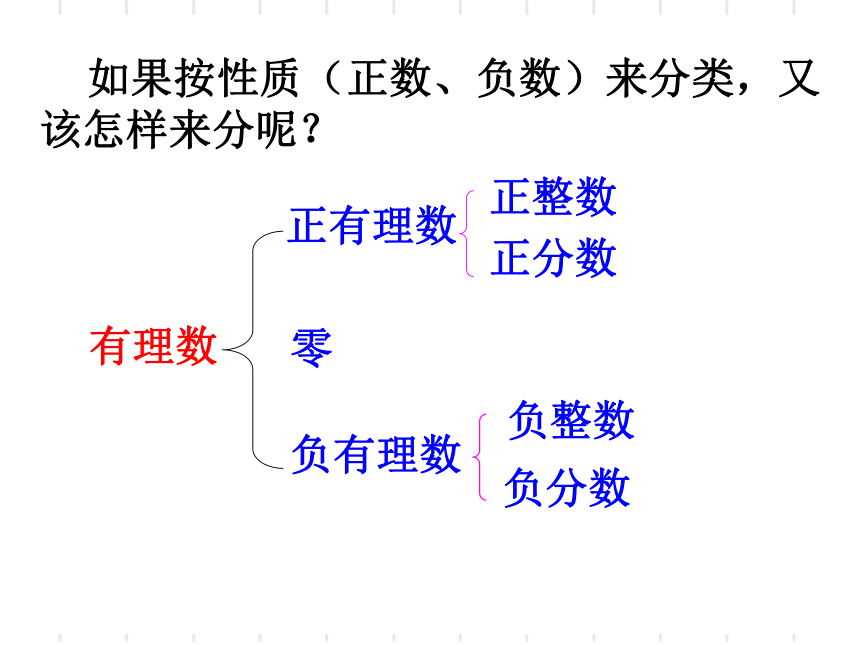
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
如果按性质(正数、负数)来分类,又该怎样来分呢?
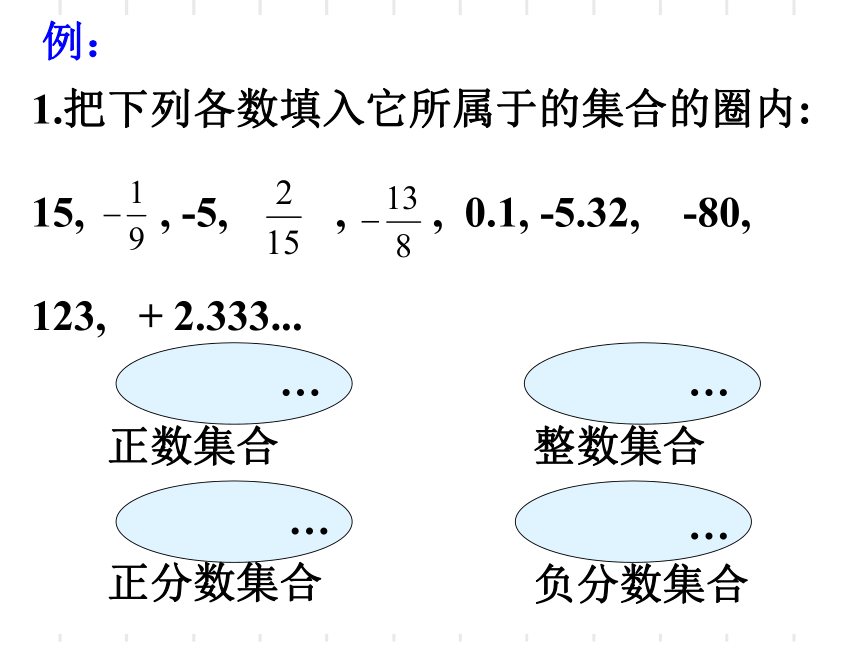
例:
1.把下列各数填入它所属于的集合的圈内:
15,
,
-5,
,
,
0.1,
-5.32,
-80,
123,
+
2.333...
正数集合
正分数集合
整数集合
负分数集合
…
…
…
…
1.在下表适当的空格里画上“√”号
有理数
整数
分数
正整数
负分数
自然数
-9
-2.35
0
+5
练习:
2.下列各数:-2,5,
,0.63,0,7,-0.05,
-6,9,
,
其中正数有__个,负数有__个,正分数有__个,负分数有__个,自然数有__个,整数有__个。
6
6
4
2
3
4
3.给出下列说法:
①0是整数;②
是负分数;③4.2不是正数;④自然数一定是正数;⑤负分数一定是负有理数。
其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
C
注意:1.由于有限小数和无限循环小数都可以化成分数所以他们也是分数,当然是有理数!
2.有些数是不能化成分数的,也不是整数,不是有理数!如π(无限不循环小数)
整数
和
分数
统称为有理数。
思考?
是不是有理数?
非负整数=非负数的整数=自然数
其他一些概念:
非负数=非负数的数=正数+0
非正数?非正整数?
零是(
)
A.最大的非正有理数
B.最小的整数
C.最小的非正有理数
D.最小的有理数
1、把下列各数填入相应的集合内。
,-3.1416,0,2008,
,-0.23456,
10%,10.1,0.67,-89
……
……
正数集合
负数集合
……
……
整数集合
分数集合
,2008
10.1
,
0.67
-3.1416,
-0.23456,
-89
,10%,
0,
2008,
-89
,-3.1416,
-0.23456,
10%
,10.1,
0.67
练习:
(1)0是整数而不是正数(
)
(2)自然数一定是整数(
)
(3)0一定是正整数(
)
(4)整数一定是自然数(
)
√
√
×
×
2.判
断:
3.下列说法中,正确的是(
)
A、正整数、负整数统称为整数
B、正分数、负分数统称为分数
C、零既可以是正整数,也可以是负整数
D、一个有理数不是正数就是负数
B
4、既是分数又是正数的是(
)
A.+2
B.-
C.0
D.2.3
5、把下列各数填在表示相应集合的大括号中.
+6,-8,25,-0.4,0,-
,9.15,
整数集合{
…};
分数集合{
…
};
非负数集合
{
…};
正数集合{
…};负数集{
…}
.
非正整数?非负分数?
D
+6,-8,25,0
-0.4,
-
,9.15,
+6,25,0,9.15,
+6,25,
9.15,
-8,-0.4,-
小结
1、有理数的概念;
2、有理数的分类。
1.2.1有理数
我们学过的数:
正整数,如:1、2、3……
零,0
负整数,如:-1、-2、-3
……
正分数,如:
、
、
、0.1、5.32……
负分数,如:
、
、
-0.5、
-150.32……
整
数
分
数
正整数、零、负整数统称为整数。
正分数、负分数统称为分数。
整数和分数统称为有理数。
有理数可以怎样分类呢?
有
理
数
整数
分数
正整数
零
负整数
正分数
负分数
自然数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
如果按性质(正数、负数)来分类,又该怎样来分呢?
例:
1.把下列各数填入它所属于的集合的圈内:
15,
,
-5,
,
,
0.1,
-5.32,
-80,
123,
+
2.333...
正数集合
正分数集合
整数集合
负分数集合
…
…
…
…
1.在下表适当的空格里画上“√”号
有理数
整数
分数
正整数
负分数
自然数
-9
-2.35
0
+5
练习:
2.下列各数:-2,5,
,0.63,0,7,-0.05,
-6,9,
,
其中正数有__个,负数有__个,正分数有__个,负分数有__个,自然数有__个,整数有__个。
6
6
4
2
3
4
3.给出下列说法:
①0是整数;②
是负分数;③4.2不是正数;④自然数一定是正数;⑤负分数一定是负有理数。
其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
C
注意:1.由于有限小数和无限循环小数都可以化成分数所以他们也是分数,当然是有理数!
2.有些数是不能化成分数的,也不是整数,不是有理数!如π(无限不循环小数)
整数
和
分数
统称为有理数。
思考?
是不是有理数?
非负整数=非负数的整数=自然数
其他一些概念:
非负数=非负数的数=正数+0
非正数?非正整数?
零是(
)
A.最大的非正有理数
B.最小的整数
C.最小的非正有理数
D.最小的有理数
1、把下列各数填入相应的集合内。
,-3.1416,0,2008,
,-0.23456,
10%,10.1,0.67,-89
……
……
正数集合
负数集合
……
……
整数集合
分数集合
,2008
10.1
,
0.67
-3.1416,
-0.23456,
-89
,10%,
0,
2008,
-89
,-3.1416,
-0.23456,
10%
,10.1,
0.67
练习:
(1)0是整数而不是正数(
)
(2)自然数一定是整数(
)
(3)0一定是正整数(
)
(4)整数一定是自然数(
)
√
√
×
×
2.判
断:
3.下列说法中,正确的是(
)
A、正整数、负整数统称为整数
B、正分数、负分数统称为分数
C、零既可以是正整数,也可以是负整数
D、一个有理数不是正数就是负数
B
4、既是分数又是正数的是(
)
A.+2
B.-
C.0
D.2.3
5、把下列各数填在表示相应集合的大括号中.
+6,-8,25,-0.4,0,-
,9.15,
整数集合{
…};
分数集合{
…
};
非负数集合
{
…};
正数集合{
…};负数集{
…}
.
非正整数?非负分数?
D
+6,-8,25,0
-0.4,
-
,9.15,
+6,25,0,9.15,
+6,25,
9.15,
-8,-0.4,-
小结
1、有理数的概念;
2、有理数的分类。
