人教版八年级上册12.2 三角形全等的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册12.2 三角形全等的判定 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 181.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 15:51:19 | ||
图片预览



文档简介
三角形全等的判定
同步练习
一.选择题(共12小题)
1.下列条件中,不能判定△ABC与△DEF一定全等的是( )
A.AB=DE,BC=EF,∠A=∠D=90°
B.AB=DE,BC=EF,∠A=∠D=80°
C.AB=DE,∠A=∠D=90°,∠B=∠E=40°
D.BC=EF,∠A=∠D=80°,∠B=∠E=40°
2.如图,线段AD与BC相交于点O,连接AB、CD,且OB=OC,要使△AOB≌△DOC,应添加一个条件,不能证明△MOB≌△COD的是( )
A.∠A=∠D
B.AO=DO
C.∠B=∠C
D.AB=CD
3.如图,AC与DB交于点O,下列条件不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.∠A=∠D,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠ACB=∠DBC
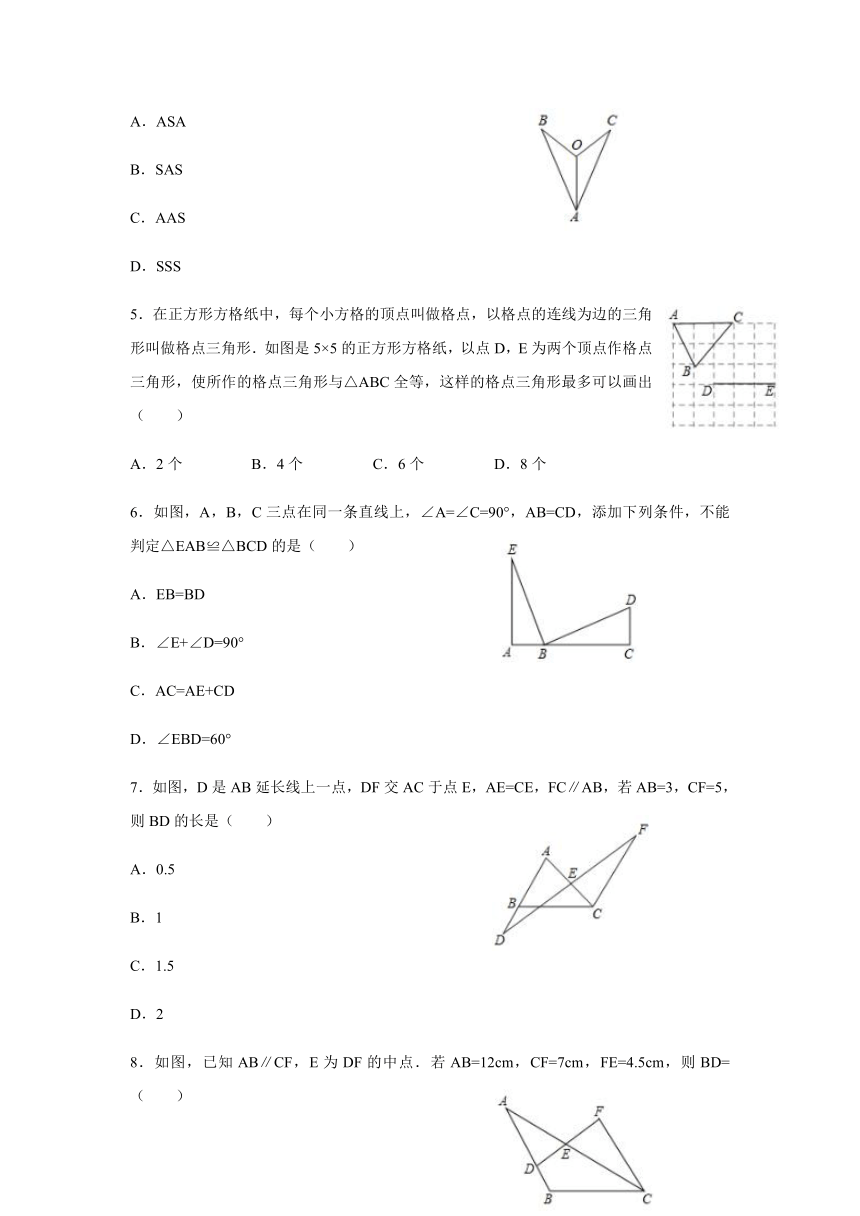
4.在一次小制作活动中,艳艳剪了一个燕尾图案(如图所示),她用刻度尺量得AB=AC,BO=CO,为了保证图案的美观,她准备再用量角器量一下∠B和∠C是否相等,小麦走过来说:“不用量了,肯定相等”,小麦的说法利用了判定三角形全等的方法是( )
A.ASA
B.SAS
C.AAS
D.SSS
5.在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个
B.4个
C.6个
D.8个
6.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,添加下列条件,不能判定△EAB≌△BCD的是( )
A.EB=BD
B.∠E+∠D=90°
C.AC=AE+CD
D.∠EBD=60°
7.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5
B.1
C.1.5
D.2
8.如图,已知AB∥CF,E为DF的中点.若AB=12cm,CF=7cm,FE=4.5cm,则BD=( )
A.5cm
B.6cm
C.7cm
D.4.5cm
9.如图,线段AB与CD相交于点O,AO=BO,CO=DO,BC⊥CD,若BC=6,AC=10,则CD的长为( )
A.6
B.7
C.8
D.9
10.如图,AD∥BC,点E是线段AB的中点,DE平分∠ADC,BC=AD+2,CD=7,则BC2-AD2的值等于( )
A.14
B.9
C.8
D.5
11.如图,已知,AB=AD,∠ACB=∠AED,∠DAB=∠EAC,则下列结论错误的是( )
A.∠B=∠ADE
B.BC=AE
C.∠ACE=∠AEC
D.∠CDE=∠BAD
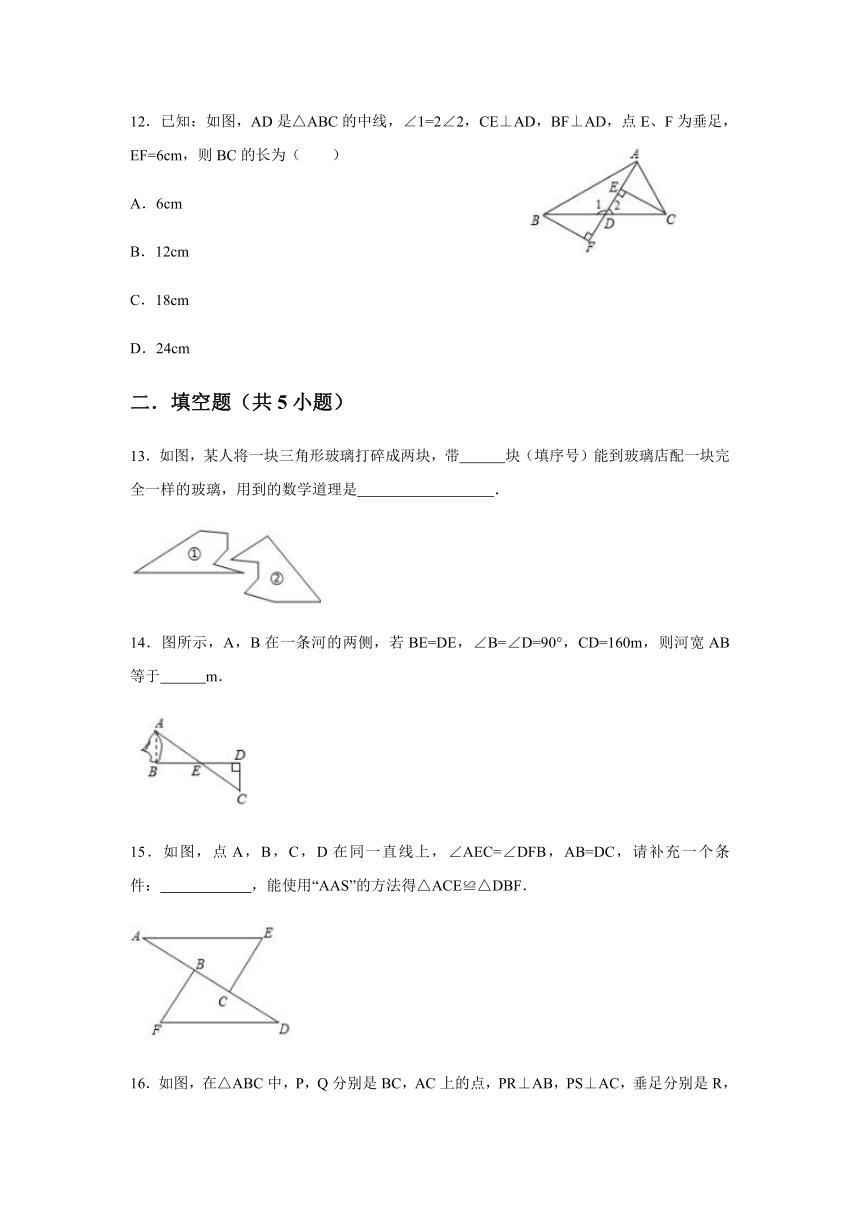
12.已知:如图,AD是△ABC的中线,∠1=2∠2,CE⊥AD,BF⊥AD,点E、F为垂足,EF=6cm,则BC的长为( )
A.6cm
B.12cm
C.18cm
D.24cm
二.填空题(共5小题)
13.如图,某人将一块三角形玻璃打碎成两块,带
块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是
.
14.图所示,A,B在一条河的两侧,若BE=DE,∠B=∠D=90°,CD=160m,则河宽AB等于
m.
15.如图,点A,B,C,D在同一直线上,∠AEC=∠DFB,AB=DC,请补充一个条件:
,能使用“AAS”的方法得△ACE≌△DBF.
16.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,那么下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④BR=QS,其中一定正确的是(填写编号)
.
17.如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠AFE;②BF=DE:③∠BFE=∠BAE;④∠BFD=∠CAF.其中正确的结论是
.(填写所正确结论的序号).
三.解答题(共5小题)
18.如图所示,O是线段AC、BD的交点,并且AC=BD,AB=CD.小明认为证明图中的△AOB和△DOC全等,他说连接BC或AD就可以了,请你用一种方法试一试看.
19.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:
(1)△AEH≌△BEC.(2)AH=2BD.
20.如图,点A,F,D,C在同一直线上,BC,EF交于点M,∠B=∠E=90°,AF=CD,AB=DE.求证:(1)Rt△ABC≌Rt△DEF;(2)MF=MC.
21.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
22.如图,在△ABC中,AB=AC=3,∠B=∠C=50°,点D在边BC上运动(点D不与点B,C重合),连接AD,作∠ADE=50°,DE交边AC于点E.
(1)当∠BDA=100°时,∠EDC=
°,∠DEC=
°.
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
参考答案
1-5:BDDDB
6-10:DDACA
11-12:BB
:②,ASA
160°
∠A=∠D
①②
①③④
18、证明:连接BC,在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),
∴∠A=∠D,
又在△AOB和△DOC中
∴△AOB≌△DOC(AAS).
19、:(1)∵AD⊥BC,
∴∠DAC+∠C=90°,
∵BE⊥AC,
∴∠EBC+∠C=90°,
∴∠DAC=∠EBC,
在△AEH与△BEC中,
∴△AEH≌△BEC(ASA);
(2)∵△AEH≌△BEC,
∴AH=BC,
∵AB=AC,AD⊥BC,
∴BC=2BD,
∴AH=2BD.
20、(1)证明:∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF,
∵∠B=∠E=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL);
(2)证明:由(1)知,Rt△ABC≌Rt△DEF,
∴∠BCA=∠EFD,
∴∠MCF=∠MFC,
∴MF=MC.
21、:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°;
(2)∠1=∠2,
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,
∴∠1=∠2.
22、:(1)∵∠BDA=100°,∠ADE=50°,
∴∠ED=180°-100°-50°=30°,
∵∠C=50°,
∴∠DEC=180°-50°-30°=100°,
故答案为:30,100;
(2)当DC=3时,△ABD≌△DCE,理由如下:
∵AB=3,DC=3,
∴AB=DC,
∵∠B=50°,∠ADE=50°,
∴∠B=∠ADE,
∵∠ADB+∠ADE+∠EDC=180°∠DEC+∠C+∠EDC=180°,
∴∠ADB=∠DEC,
在△ABD和△DCE中
∴△ABD≌△DCE;
(3)可以,理由如下:
∵∠B=∠C=50°,∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-50°-50°=80°,
分三种情况讨论:
①当DA=DE时,∠DAE=∠DEA,
∵∠ADE=50°,∠ADE+∠DAE+∠DEA=180°,
∴∠DAE=(180°-50°)÷2=65°,
∴∠BAD=∠BAC-∠DAE=80°-65°=15°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°-∠B-∠BAD=180°-50°-15°=115°
②当AD=AE时,∠AED=∠ADE=50°
∵∠ADE+∠AED+∠DAE=180°
∴∠DAE=180°-∠AED-∠ADE=180°-50°-50°=80°,
又∵∠BAC=80°,
∴∠DAE=∠BAE,
∴点D与点B重合,不合题意.
③当EA=ED时,∠DAE=∠ADE=50°,
∴∠BAD=∠BAC-∠DAE=80°-50°=30°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°-∠B-∠BAD=180°-50°-30°=100°,
综上所述,当∠BDA的度数为115°或100°时,△ADE是等腰三角形
同步练习
一.选择题(共12小题)
1.下列条件中,不能判定△ABC与△DEF一定全等的是( )
A.AB=DE,BC=EF,∠A=∠D=90°
B.AB=DE,BC=EF,∠A=∠D=80°
C.AB=DE,∠A=∠D=90°,∠B=∠E=40°
D.BC=EF,∠A=∠D=80°,∠B=∠E=40°
2.如图,线段AD与BC相交于点O,连接AB、CD,且OB=OC,要使△AOB≌△DOC,应添加一个条件,不能证明△MOB≌△COD的是( )
A.∠A=∠D
B.AO=DO
C.∠B=∠C
D.AB=CD
3.如图,AC与DB交于点O,下列条件不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.∠A=∠D,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠ACB=∠DBC
4.在一次小制作活动中,艳艳剪了一个燕尾图案(如图所示),她用刻度尺量得AB=AC,BO=CO,为了保证图案的美观,她准备再用量角器量一下∠B和∠C是否相等,小麦走过来说:“不用量了,肯定相等”,小麦的说法利用了判定三角形全等的方法是( )
A.ASA
B.SAS
C.AAS
D.SSS
5.在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个
B.4个
C.6个
D.8个
6.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,添加下列条件,不能判定△EAB≌△BCD的是( )
A.EB=BD
B.∠E+∠D=90°
C.AC=AE+CD
D.∠EBD=60°
7.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5
B.1
C.1.5
D.2
8.如图,已知AB∥CF,E为DF的中点.若AB=12cm,CF=7cm,FE=4.5cm,则BD=( )
A.5cm
B.6cm
C.7cm
D.4.5cm
9.如图,线段AB与CD相交于点O,AO=BO,CO=DO,BC⊥CD,若BC=6,AC=10,则CD的长为( )
A.6
B.7
C.8
D.9
10.如图,AD∥BC,点E是线段AB的中点,DE平分∠ADC,BC=AD+2,CD=7,则BC2-AD2的值等于( )
A.14
B.9
C.8
D.5
11.如图,已知,AB=AD,∠ACB=∠AED,∠DAB=∠EAC,则下列结论错误的是( )
A.∠B=∠ADE
B.BC=AE
C.∠ACE=∠AEC
D.∠CDE=∠BAD
12.已知:如图,AD是△ABC的中线,∠1=2∠2,CE⊥AD,BF⊥AD,点E、F为垂足,EF=6cm,则BC的长为( )
A.6cm
B.12cm
C.18cm
D.24cm
二.填空题(共5小题)
13.如图,某人将一块三角形玻璃打碎成两块,带
块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是
.
14.图所示,A,B在一条河的两侧,若BE=DE,∠B=∠D=90°,CD=160m,则河宽AB等于
m.
15.如图,点A,B,C,D在同一直线上,∠AEC=∠DFB,AB=DC,请补充一个条件:
,能使用“AAS”的方法得△ACE≌△DBF.
16.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,那么下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④BR=QS,其中一定正确的是(填写编号)
.
17.如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠AFE;②BF=DE:③∠BFE=∠BAE;④∠BFD=∠CAF.其中正确的结论是
.(填写所正确结论的序号).
三.解答题(共5小题)
18.如图所示,O是线段AC、BD的交点,并且AC=BD,AB=CD.小明认为证明图中的△AOB和△DOC全等,他说连接BC或AD就可以了,请你用一种方法试一试看.
19.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:
(1)△AEH≌△BEC.(2)AH=2BD.
20.如图,点A,F,D,C在同一直线上,BC,EF交于点M,∠B=∠E=90°,AF=CD,AB=DE.求证:(1)Rt△ABC≌Rt△DEF;(2)MF=MC.
21.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
22.如图,在△ABC中,AB=AC=3,∠B=∠C=50°,点D在边BC上运动(点D不与点B,C重合),连接AD,作∠ADE=50°,DE交边AC于点E.
(1)当∠BDA=100°时,∠EDC=
°,∠DEC=
°.
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
参考答案
1-5:BDDDB
6-10:DDACA
11-12:BB
:②,ASA
160°
∠A=∠D
①②
①③④
18、证明:连接BC,在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),
∴∠A=∠D,
又在△AOB和△DOC中
∴△AOB≌△DOC(AAS).
19、:(1)∵AD⊥BC,
∴∠DAC+∠C=90°,
∵BE⊥AC,
∴∠EBC+∠C=90°,
∴∠DAC=∠EBC,
在△AEH与△BEC中,
∴△AEH≌△BEC(ASA);
(2)∵△AEH≌△BEC,
∴AH=BC,
∵AB=AC,AD⊥BC,
∴BC=2BD,
∴AH=2BD.
20、(1)证明:∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF,
∵∠B=∠E=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL);
(2)证明:由(1)知,Rt△ABC≌Rt△DEF,
∴∠BCA=∠EFD,
∴∠MCF=∠MFC,
∴MF=MC.
21、:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°;
(2)∠1=∠2,
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,
∴∠1=∠2.
22、:(1)∵∠BDA=100°,∠ADE=50°,
∴∠ED=180°-100°-50°=30°,
∵∠C=50°,
∴∠DEC=180°-50°-30°=100°,
故答案为:30,100;
(2)当DC=3时,△ABD≌△DCE,理由如下:
∵AB=3,DC=3,
∴AB=DC,
∵∠B=50°,∠ADE=50°,
∴∠B=∠ADE,
∵∠ADB+∠ADE+∠EDC=180°∠DEC+∠C+∠EDC=180°,
∴∠ADB=∠DEC,
在△ABD和△DCE中
∴△ABD≌△DCE;
(3)可以,理由如下:
∵∠B=∠C=50°,∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-50°-50°=80°,
分三种情况讨论:
①当DA=DE时,∠DAE=∠DEA,
∵∠ADE=50°,∠ADE+∠DAE+∠DEA=180°,
∴∠DAE=(180°-50°)÷2=65°,
∴∠BAD=∠BAC-∠DAE=80°-65°=15°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°-∠B-∠BAD=180°-50°-15°=115°
②当AD=AE时,∠AED=∠ADE=50°
∵∠ADE+∠AED+∠DAE=180°
∴∠DAE=180°-∠AED-∠ADE=180°-50°-50°=80°,
又∵∠BAC=80°,
∴∠DAE=∠BAE,
∴点D与点B重合,不合题意.
③当EA=ED时,∠DAE=∠ADE=50°,
∴∠BAD=∠BAC-∠DAE=80°-50°=30°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°-∠B-∠BAD=180°-50°-30°=100°,
综上所述,当∠BDA的度数为115°或100°时,△ADE是等腰三角形
