人教版九年级数学上册22.1.3 二次函数y=ax2 k的图象和性质课件(17张)
文档属性
| 名称 | 人教版九年级数学上册22.1.3 二次函数y=ax2 k的图象和性质课件(17张) | 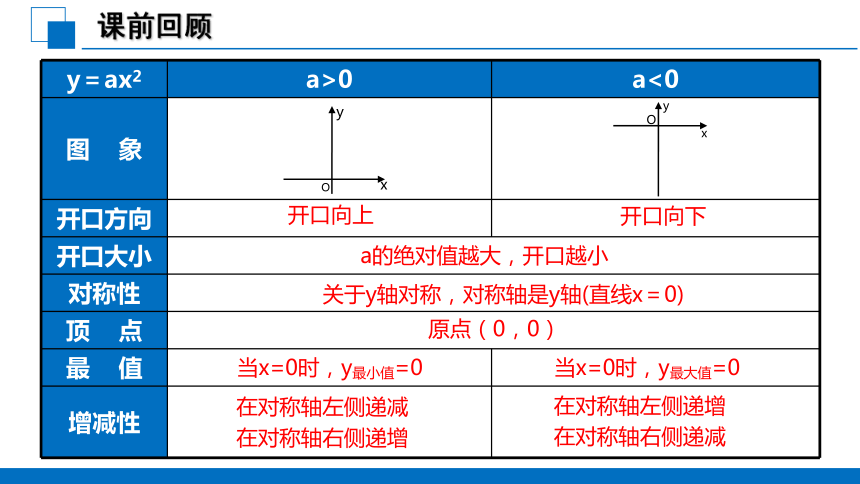 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 18:40:46 | ||
图片预览







文档简介
(共21张PPT)
y=ax2
a>0
a<0
图
象
开口方向
开口大小
对称性
顶
点
最
值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称,对称轴是y轴(直线x=0)
原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
课前回顾
第二十二章
二次函数
22.1
二次函数的图象和性质
第3课时
二次函数y=ax2+k的图象和性质
灵宝市秦岭学校
周
兵
1
会画二次函数y=ax2+k的图象.(重点)
2
掌握二次函数y=ax2+k的性质并会应用.
(难点)
学习目标
2
理解y=ax?与
y=ax?+k之间的联系.(重点)
一、二次函数y=ax2+k的图象
动手操作:在同一直角坐标系中,画出二次函数y=x2+1,y=x2-1的图象。
解:列表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2+1
…
…
y=x2-1
…
…
10
5
2
1
2
5
10
8
3
0
-1
0
3
8
y=x2+1
10
8
6
4
2
-2
-5
5
x
y
y=x2-1
一、二次函数y=ax2+k的图象
(1)抛物线y=x2+1、y=x2-1的开口方向、对称轴、顶点
各是什么?
观察发现
抛物线
开口方向
对称轴
顶点坐标
y=x2+1
向上
y轴
(0,1)
y=x2-1
向上
y轴
(0,-1)
y=x2+1
10
8
6
4
2
-2
-5
5
x
y
y=x2-1
一、二次函数y=ax2+k的图象
(2)抛物线y=x2+1、y=x2-1与y=x2抛物线有什么关系?
观察发现
y=x2+1
10
8
6
4
2
-2
-5
5
x
y
y=x2-1
y=x2
把抛物线y=x2向上平移1个单位,就得到抛物线y=x2+1。
把抛物线y=x2向下平移1个单位,就得到抛物线y=x2-1。
问题:把抛物线y=2x2向上平移5个单位,会得到
哪条抛物线?向下平移3.4个单位呢?
一、二次函数y=ax2+k的图象
二次函数y=ax2+k的图象可以由
y=ax2
的图象平移得到:
当k
>
0
时,向上平移|k|个单位长度得到.
当k
<
0
时,向下平移|k|个单位长度得到.
二次函数y=ax2
与y=ax2+k(a
≠
0)的图象的关系
上下平移规律:
平方项不变,常数项上加下减.
知识要点
一、二次函数y=ax2+k的图象
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
2
y=-0.5x2
y=-0.5x2+2
y=-0.5x2-2
思考:
1、观察在同一直角坐标系中,画出的
y=-0.5x2,y=-0.5x2+2
,
y=-0.5x2-2
的函数图象,说说三条抛物线的相互关系,
2、尝试总结抛物线y=ax2+k的性质,并在小组内交流。
y=ax2+k
a>0
a<0
图
象
开口方向
开口大小
对称性
顶
点
最
值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称,对称轴是y轴(直线x=0)
(0,k)
当x=0时,y最小值=k
当x=0时,y最大值=k
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
一、二次函数y=ax2+k的图象与性质
反馈练习
1、把抛物线y=-2x2向上平移3个单位长度,得到的抛物线是
。
2、把抛物线y=-x2-2向下平移5个单位,得到的抛物线是
。
3、若一条抛物线向上平移2.5个单位后得到抛物线y=0.5x2,
则原抛物线是
。
4、分别说下列抛物线的开口方向,对称轴、顶点坐标、最大值或最小值及增减性如何?
(1)y=-x2-3
(2)y=1.5x2+7
(3)y=2x2-1
(4)
y=
?2x2+3
y=-2x2+3
y=-x2-7
y=0.5x2-2.5
反馈练习
5.(1)抛物线y=?2x2+3的顶点坐标是
,对称轴是
,在
侧,y随着x的增大而增大;在
侧,y随着x的增大而减小,当x=
时,函数y的值最大,最大值是
,它是由抛物线y=?2x2向
平移
个单位得到的.
(2)抛物线
y=
x?-5
的顶点坐标是
,对称轴是
,在对称轴的左侧,y随着x的
;在对称轴的右侧,y随着x的
,当x=____时,函数y的值最
,最值是
.
(0,3)
y轴
对称轴左
对称轴右
0
3
上
3
(0,-5)
y轴
增大而减小
增大而增大
0
小
-5
反馈练习
6.函数y=3x2+5与y=3x2的图象的不同之处是(
)
A.对称轴
B.开口方向
C.顶点
D.形状
7.已知抛物线y=2x2–1上有两点(x1,y1
)
,(x2,y2)且x1<x2<0,
则y1
y2(填“<”或“>”)
8.抛物线
共有的性质是(
)
A.开口向上
B.对称轴都是y轴
C.都有最高点
D.顶点都是原点
C
<
B
例题精讲
例3:如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴
×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±
,
此时P点坐标为(
,2),(-
,2);
当b=-2时,x2-4=-2,解得x=±
,
此时P点坐标为(
,2),(-
,2).
课前小结
二次函数y=ax2+k(a≠0)的图象和性质
图象
性质
与y=ax2的关系
开口方向由a的符号决定;
k决定顶点位置;
对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
k正向上;
k负向下.
课堂检测
1.抛物线y=2x2向下平移4个单位,就得到抛物线
.
2.填表:
y
=
2x2-4
函数
开口方向
顶点
对称轴
有最高(低)点
y
=
3x2
y
=
3x2+1
y
=
-4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y轴
y轴
y轴
有最低点
有最低点
有最高点
课堂检测
3.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图象大致为( )
方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.
D
课堂检测
能力提升:
1.对于二次函数y=(m+1)xm2-m+3,当x>0时y随x的增大而增大,则m=____.
2.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)
则a=____.
3.抛物线y=ax2+c与x轴交于A(-2,0)﹑B两点,与y轴交于点C(0,-4),则三角形ABC的面积是_______.
2
-2
8
y=ax2
a>0
a<0
图
象
开口方向
开口大小
对称性
顶
点
最
值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称,对称轴是y轴(直线x=0)
原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
课前回顾
第二十二章
二次函数
22.1
二次函数的图象和性质
第3课时
二次函数y=ax2+k的图象和性质
灵宝市秦岭学校
周
兵
1
会画二次函数y=ax2+k的图象.(重点)
2
掌握二次函数y=ax2+k的性质并会应用.
(难点)
学习目标
2
理解y=ax?与
y=ax?+k之间的联系.(重点)
一、二次函数y=ax2+k的图象
动手操作:在同一直角坐标系中,画出二次函数y=x2+1,y=x2-1的图象。
解:列表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2+1
…
…
y=x2-1
…
…
10
5
2
1
2
5
10
8
3
0
-1
0
3
8
y=x2+1
10
8
6
4
2
-2
-5
5
x
y
y=x2-1
一、二次函数y=ax2+k的图象
(1)抛物线y=x2+1、y=x2-1的开口方向、对称轴、顶点
各是什么?
观察发现
抛物线
开口方向
对称轴
顶点坐标
y=x2+1
向上
y轴
(0,1)
y=x2-1
向上
y轴
(0,-1)
y=x2+1
10
8
6
4
2
-2
-5
5
x
y
y=x2-1
一、二次函数y=ax2+k的图象
(2)抛物线y=x2+1、y=x2-1与y=x2抛物线有什么关系?
观察发现
y=x2+1
10
8
6
4
2
-2
-5
5
x
y
y=x2-1
y=x2
把抛物线y=x2向上平移1个单位,就得到抛物线y=x2+1。
把抛物线y=x2向下平移1个单位,就得到抛物线y=x2-1。
问题:把抛物线y=2x2向上平移5个单位,会得到
哪条抛物线?向下平移3.4个单位呢?
一、二次函数y=ax2+k的图象
二次函数y=ax2+k的图象可以由
y=ax2
的图象平移得到:
当k
>
0
时,向上平移|k|个单位长度得到.
当k
<
0
时,向下平移|k|个单位长度得到.
二次函数y=ax2
与y=ax2+k(a
≠
0)的图象的关系
上下平移规律:
平方项不变,常数项上加下减.
知识要点
一、二次函数y=ax2+k的图象
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
2
y=-0.5x2
y=-0.5x2+2
y=-0.5x2-2
思考:
1、观察在同一直角坐标系中,画出的
y=-0.5x2,y=-0.5x2+2
,
y=-0.5x2-2
的函数图象,说说三条抛物线的相互关系,
2、尝试总结抛物线y=ax2+k的性质,并在小组内交流。
y=ax2+k
a>0
a<0
图
象
开口方向
开口大小
对称性
顶
点
最
值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称,对称轴是y轴(直线x=0)
(0,k)
当x=0时,y最小值=k
当x=0时,y最大值=k
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
一、二次函数y=ax2+k的图象与性质
反馈练习
1、把抛物线y=-2x2向上平移3个单位长度,得到的抛物线是
。
2、把抛物线y=-x2-2向下平移5个单位,得到的抛物线是
。
3、若一条抛物线向上平移2.5个单位后得到抛物线y=0.5x2,
则原抛物线是
。
4、分别说下列抛物线的开口方向,对称轴、顶点坐标、最大值或最小值及增减性如何?
(1)y=-x2-3
(2)y=1.5x2+7
(3)y=2x2-1
(4)
y=
?2x2+3
y=-2x2+3
y=-x2-7
y=0.5x2-2.5
反馈练习
5.(1)抛物线y=?2x2+3的顶点坐标是
,对称轴是
,在
侧,y随着x的增大而增大;在
侧,y随着x的增大而减小,当x=
时,函数y的值最大,最大值是
,它是由抛物线y=?2x2向
平移
个单位得到的.
(2)抛物线
y=
x?-5
的顶点坐标是
,对称轴是
,在对称轴的左侧,y随着x的
;在对称轴的右侧,y随着x的
,当x=____时,函数y的值最
,最值是
.
(0,3)
y轴
对称轴左
对称轴右
0
3
上
3
(0,-5)
y轴
增大而减小
增大而增大
0
小
-5
反馈练习
6.函数y=3x2+5与y=3x2的图象的不同之处是(
)
A.对称轴
B.开口方向
C.顶点
D.形状
7.已知抛物线y=2x2–1上有两点(x1,y1
)
,(x2,y2)且x1<x2<0,
则y1
y2(填“<”或“>”)
8.抛物线
共有的性质是(
)
A.开口向上
B.对称轴都是y轴
C.都有最高点
D.顶点都是原点
C
<
B
例题精讲
例3:如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴
×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±
,
此时P点坐标为(
,2),(-
,2);
当b=-2时,x2-4=-2,解得x=±
,
此时P点坐标为(
,2),(-
,2).
课前小结
二次函数y=ax2+k(a≠0)的图象和性质
图象
性质
与y=ax2的关系
开口方向由a的符号决定;
k决定顶点位置;
对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
k正向上;
k负向下.
课堂检测
1.抛物线y=2x2向下平移4个单位,就得到抛物线
.
2.填表:
y
=
2x2-4
函数
开口方向
顶点
对称轴
有最高(低)点
y
=
3x2
y
=
3x2+1
y
=
-4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y轴
y轴
y轴
有最低点
有最低点
有最高点
课堂检测
3.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图象大致为( )
方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.
D
课堂检测
能力提升:
1.对于二次函数y=(m+1)xm2-m+3,当x>0时y随x的增大而增大,则m=____.
2.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)
则a=____.
3.抛物线y=ax2+c与x轴交于A(-2,0)﹑B两点,与y轴交于点C(0,-4),则三角形ABC的面积是_______.
2
-2
8
同课章节目录
