苏科版八年级上册第二章轴对称图形 章节专题训练(含7个专题,word版无答案 )
文档属性
| 名称 | 苏科版八年级上册第二章轴对称图形 章节专题训练(含7个专题,word版无答案 ) |  | |
| 格式 | zip | ||
| 文件大小 | 979.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 11:23:47 | ||
图片预览




文档简介
苏科版八年级上册轴对称章节专题训练
专题一:等腰三角形中的多解问题
1.有个等腰三角形的两条边分别为4cm和8cm,则这个三角形的周长为
cm.
2.等腰三角形的一边长为2,周长为5,那么它的腰长为
cm.
3.在等腰三角形ABC中,AB=AC,∠BAC=20°,点D在直线BC上,且CD=AC,连接AD,则∠ADC=
.
4.已知等边三角形ABC的边长为3,点E在直线AB上,点D在直线CB上,且ED=EC,若AE=6,则CD的长为
.
5.在等腰三角形ABC中,BD是AC边上的高,且,则等腰三角形ABC的底角度数为
.
6.(1)等腰三角形的一个角为50°,则这个等腰三角形的底角为
.
(2)已知一个等腰三角形的一个外角为130°,则它的顶角的度数为
.
7.如图,已知点C是线段AB的中点,点
D是线段BC上的定点(不同于点B,C),过点D作直线垂直于线段AB,若点P是直线上的任一点,连接PA,PB,则能使△PAB称为等腰三角形的点P一共有
.个(填写确切数字).
8.已知等腰三角形的底边长为10cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长为5cm,那么这个三角形的腰长为
cm.
9.已知等腰三角形一腰上的中线把它的周长分为12cm和15cm两部分,则它的三边长是
cm.
10.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=80°,求∠CAD的度数.
11.以正方形ABCD的一边CD为边做等边三角形CDE.连接AE、BE.
(1)画出图形;
(2)求∠AEB的度数.
专题二:各类作图题
1.如图,点A、B、C处是新建的三个居民小区,我们要在到三个小区的距离相等的地方修建一所学校,试确定学校的位置.
2.如图,已知直线及其两侧的两点A、B.
(1)在直线上求一点P,使PA=PB;
(2)在直线上求一点Q,使平分∠AQB;
(3)在直线上求一点O,使到AB两点之间的距离之和最小.
(1)
(2)
(3)
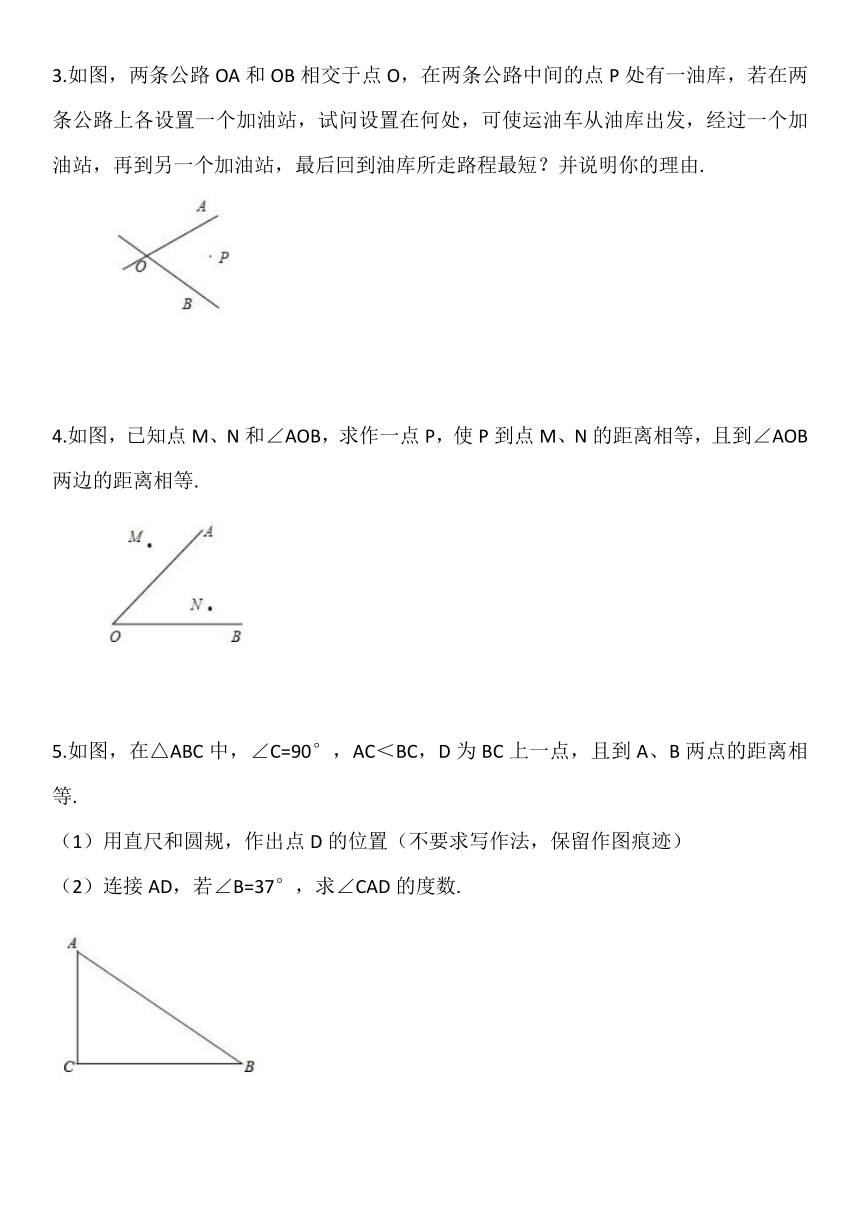
3.如图,两条公路OA和OB相交于点O,在两条公路中间的点P处有一油库,若在两条公路上各设置一个加油站,试问设置在何处,可使运油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走路程最短?并说明你的理由.
4.如图,已知点M、N和∠AOB,求作一点P,使P到点M、N的距离相等,且到∠AOB两边的距离相等.
5.如图,在△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不要求写作法,保留作图痕迹)
(2)连接AD,若∠B=37°,求∠CAD的度数.
6.如图,已知P为∠AOB内部任意一点,分别在OA、OB上,求作P1、P2,使△PP1P2的周长最小.
7.(1)如图(1),在AB直线一侧有C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由;
(2)如图(2),在∠AOB内部找一点P,是否存在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由;
(3)如图(3),在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N四点组成周长最短,找出E、F两点,并说明理由.
8.如图,直线表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?
专题三:角平分线与垂直平分线相关的辅助线
1.如图,AB=CD,AC、BD的垂直平分线EM、EN相交于点E.求证:∠ABE=∠CDE.
2.如图,在△ABC中,D为BC的的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB交于点F,EG⊥AC交AC的延长线于点G.试问:BF与CG的大小关系如何?证明你的结论.
3.如图,D为∠ABC内一点,点M在边BA上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.
4.已知:如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E,求证:∠ABE=∠CDE.
5.如图,在△ABC中,O是∠ABC,∠ACB的平分线的交点,O′是∠ABC,∠ACB外角的平分线的交点.
(1)点O′在∠A的平分线上吗?为什么?
(2)求证:∠BOC+∠BO′C=180°.
专题四:轴对称与三角形相关的面积问题
1.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积是(
)
A.
15
B.
30
C.
45
D.
60
2.如图,BD是∠ABC的角平分线,DE⊥AB于点E,△ABC的面积是30cm?,AB=8cm,BC=7cm,则DE=
.
3.如图,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是
.
4.如图,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,AB=6,BC=8.如果,那么DE=
.
5.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则=
.
6.如图,已知△ABC的周长是20,OC、OB分别平分∠ABC和∠ACB,OD⊥BC于点D,若△ABC的面积是30,则OD=
.
7.如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,求BC的长.
专题五:直角三角形斜边上的中线等于斜边的一半
1.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,E为AC的中点,连接DE,则三角形CDE的周长为
.
2.
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长为
.
3.如图,BE、CF是△ABC的两条高,M为BC的中点,若EF=5,BC=8,则△EFM的周长是
.
4.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC保持不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.当∠BAE=90°,AF=5时,CD的长为
.
5.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,则AC的长为
.
6.如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,如果∠BEC=80°,那么∠GHE等于
.
7.如图,△ABC中,∠ACB=90°,D在BC上,E为AB中点,AD,CE相交于F,AD=DB.若∠B=35°,则∠DFE=
.
8.如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为
.
9.如图,在△ABC中,点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=;
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
10.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10,EF=4.
(1)求△MEF的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
专题六:直角三角形30°所对的直角边是斜边的一半
1.如图,AC=BC=10cm,∠B=15°,AD⊥BC于点D,则AD的长为
.
2.如图,∠AOB=30°,OP平分∠AOB,PC∥OB,PD⊥OB于点D,若PD=2cm,则PC=
cm.
3.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
.
4.
如图所示,在Rt△ABC中,∠C=90°,∠B=30°,AB=6,点E在AB边上,D是BC边上一点(不与点B,C重合),且AE=ED,则线段AE的最小值是
.
5.如图,在△ABC中,∠C=60°,AD是BC边上的高,E为AD的中点,连接BE并延长交AC于点F.若∠AFB=90°,EF=2,则BF的长为
.
6.顶角为30°的等腰三角形,若腰长为2,则腰上的高为 .?
7.如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作FE⊥BC于点E,则BE的长为 .?
8.如图,∠AOP=∠BOP=15°,PC∥OB,PD⊥OA,若PC=4,则PD的长为
.
9.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
10.问题探究:如图①,在Rt△ABC中,∠ACB=90°,∠ABC=30°,为探究Rt△ABC中30°角所对的直角边AC与斜边AB的数量关系,某学习小组成员已经添加了辅助线.
(1)请叙述辅助线的添加方法,并完成探究过程.
(2)探究应用:如图②,在Rt△ABC中,∠C=90°,∠ABC=30°,点D在线段CB上,以AD为边作等边三角形ADE,连接BE,为探究线段BE与DE之间的数量关系,组长佳佳已经添加了辅助线:取AB的中点F,连接EF.则线段BE与DE之间的数量关系是 ,说明理由.?
微专题七:等腰三角形的动点多解问题
1.如图,在中,,cm,cm,若动点从点开始,按的路径运动,且速度为每秒2cm,设点运动的时间为秒.
(1)则
cm
;
(2)当平分,求此时点的运动时间的值;
(3)点运动过程中,能否成为等腰三角形?若能,求出的值;若不能请说明理由.
2.如图,在中,,动点从点出发,沿着运动,速度为每秒1个单位,到达点时运动停止,设运动时间为秒,请解答下列问题:
(1)求上的高;
(2)当为何值时,为等腰三角形?
3.如图,在中,,,,点在的延长线上,,连接.
(1)求的长;
(2)动点从点出发,向终点运动,速度为2个单位/秒,运动时间为秒.
①当为何值时,;
②当为何值时,是以为腰的等腰三角形?
4.如图,已知△ABC中,AC=6cm,BC=8cm,AB=10cm,动点P从点C出发,沿着△ABC的三条边逆时针走一圈回到C点,速度为2cm/s,设运动时间为t秒.
(1)判断△ABC的形状,并求AB边上的高;
(2)t为何值时,△ACP为等腰三角形?
(3)另有一点Q,从点C开始,按顺时针走一圈回到C点,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
5.如图,△中,,若动点从点开始,按的路径运动,且速度为每秒,设运动的时间为秒。
(1)当为何值时,把△的周长分成相等的两部分。
(2)当为何值时,把△的面积分成相等的两部分,并求出此时的长;
(3)当为何值时,△为等腰三角形?
专题一:等腰三角形中的多解问题
1.有个等腰三角形的两条边分别为4cm和8cm,则这个三角形的周长为
cm.
2.等腰三角形的一边长为2,周长为5,那么它的腰长为
cm.
3.在等腰三角形ABC中,AB=AC,∠BAC=20°,点D在直线BC上,且CD=AC,连接AD,则∠ADC=
.
4.已知等边三角形ABC的边长为3,点E在直线AB上,点D在直线CB上,且ED=EC,若AE=6,则CD的长为
.
5.在等腰三角形ABC中,BD是AC边上的高,且,则等腰三角形ABC的底角度数为
.
6.(1)等腰三角形的一个角为50°,则这个等腰三角形的底角为
.
(2)已知一个等腰三角形的一个外角为130°,则它的顶角的度数为
.
7.如图,已知点C是线段AB的中点,点
D是线段BC上的定点(不同于点B,C),过点D作直线垂直于线段AB,若点P是直线上的任一点,连接PA,PB,则能使△PAB称为等腰三角形的点P一共有
.个(填写确切数字).
8.已知等腰三角形的底边长为10cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长为5cm,那么这个三角形的腰长为
cm.
9.已知等腰三角形一腰上的中线把它的周长分为12cm和15cm两部分,则它的三边长是
cm.
10.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=80°,求∠CAD的度数.
11.以正方形ABCD的一边CD为边做等边三角形CDE.连接AE、BE.
(1)画出图形;
(2)求∠AEB的度数.
专题二:各类作图题
1.如图,点A、B、C处是新建的三个居民小区,我们要在到三个小区的距离相等的地方修建一所学校,试确定学校的位置.
2.如图,已知直线及其两侧的两点A、B.
(1)在直线上求一点P,使PA=PB;
(2)在直线上求一点Q,使平分∠AQB;
(3)在直线上求一点O,使到AB两点之间的距离之和最小.
(1)
(2)
(3)
3.如图,两条公路OA和OB相交于点O,在两条公路中间的点P处有一油库,若在两条公路上各设置一个加油站,试问设置在何处,可使运油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走路程最短?并说明你的理由.
4.如图,已知点M、N和∠AOB,求作一点P,使P到点M、N的距离相等,且到∠AOB两边的距离相等.
5.如图,在△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不要求写作法,保留作图痕迹)
(2)连接AD,若∠B=37°,求∠CAD的度数.
6.如图,已知P为∠AOB内部任意一点,分别在OA、OB上,求作P1、P2,使△PP1P2的周长最小.
7.(1)如图(1),在AB直线一侧有C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由;
(2)如图(2),在∠AOB内部找一点P,是否存在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由;
(3)如图(3),在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N四点组成周长最短,找出E、F两点,并说明理由.
8.如图,直线表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?
专题三:角平分线与垂直平分线相关的辅助线
1.如图,AB=CD,AC、BD的垂直平分线EM、EN相交于点E.求证:∠ABE=∠CDE.
2.如图,在△ABC中,D为BC的的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB交于点F,EG⊥AC交AC的延长线于点G.试问:BF与CG的大小关系如何?证明你的结论.
3.如图,D为∠ABC内一点,点M在边BA上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.
4.已知:如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E,求证:∠ABE=∠CDE.
5.如图,在△ABC中,O是∠ABC,∠ACB的平分线的交点,O′是∠ABC,∠ACB外角的平分线的交点.
(1)点O′在∠A的平分线上吗?为什么?
(2)求证:∠BOC+∠BO′C=180°.
专题四:轴对称与三角形相关的面积问题
1.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积是(
)
A.
15
B.
30
C.
45
D.
60
2.如图,BD是∠ABC的角平分线,DE⊥AB于点E,△ABC的面积是30cm?,AB=8cm,BC=7cm,则DE=
.
3.如图,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是
.
4.如图,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,AB=6,BC=8.如果,那么DE=
.
5.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则=
.
6.如图,已知△ABC的周长是20,OC、OB分别平分∠ABC和∠ACB,OD⊥BC于点D,若△ABC的面积是30,则OD=
.
7.如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,求BC的长.
专题五:直角三角形斜边上的中线等于斜边的一半
1.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,E为AC的中点,连接DE,则三角形CDE的周长为
.
2.
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长为
.
3.如图,BE、CF是△ABC的两条高,M为BC的中点,若EF=5,BC=8,则△EFM的周长是
.
4.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC保持不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.当∠BAE=90°,AF=5时,CD的长为
.
5.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,则AC的长为
.
6.如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,如果∠BEC=80°,那么∠GHE等于
.
7.如图,△ABC中,∠ACB=90°,D在BC上,E为AB中点,AD,CE相交于F,AD=DB.若∠B=35°,则∠DFE=
.
8.如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为
.
9.如图,在△ABC中,点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=;
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
10.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10,EF=4.
(1)求△MEF的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
专题六:直角三角形30°所对的直角边是斜边的一半
1.如图,AC=BC=10cm,∠B=15°,AD⊥BC于点D,则AD的长为
.
2.如图,∠AOB=30°,OP平分∠AOB,PC∥OB,PD⊥OB于点D,若PD=2cm,则PC=
cm.
3.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
.
4.
如图所示,在Rt△ABC中,∠C=90°,∠B=30°,AB=6,点E在AB边上,D是BC边上一点(不与点B,C重合),且AE=ED,则线段AE的最小值是
.
5.如图,在△ABC中,∠C=60°,AD是BC边上的高,E为AD的中点,连接BE并延长交AC于点F.若∠AFB=90°,EF=2,则BF的长为
.
6.顶角为30°的等腰三角形,若腰长为2,则腰上的高为 .?
7.如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作FE⊥BC于点E,则BE的长为 .?
8.如图,∠AOP=∠BOP=15°,PC∥OB,PD⊥OA,若PC=4,则PD的长为
.
9.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
10.问题探究:如图①,在Rt△ABC中,∠ACB=90°,∠ABC=30°,为探究Rt△ABC中30°角所对的直角边AC与斜边AB的数量关系,某学习小组成员已经添加了辅助线.
(1)请叙述辅助线的添加方法,并完成探究过程.
(2)探究应用:如图②,在Rt△ABC中,∠C=90°,∠ABC=30°,点D在线段CB上,以AD为边作等边三角形ADE,连接BE,为探究线段BE与DE之间的数量关系,组长佳佳已经添加了辅助线:取AB的中点F,连接EF.则线段BE与DE之间的数量关系是 ,说明理由.?
微专题七:等腰三角形的动点多解问题
1.如图,在中,,cm,cm,若动点从点开始,按的路径运动,且速度为每秒2cm,设点运动的时间为秒.
(1)则
cm
;
(2)当平分,求此时点的运动时间的值;
(3)点运动过程中,能否成为等腰三角形?若能,求出的值;若不能请说明理由.
2.如图,在中,,动点从点出发,沿着运动,速度为每秒1个单位,到达点时运动停止,设运动时间为秒,请解答下列问题:
(1)求上的高;
(2)当为何值时,为等腰三角形?
3.如图,在中,,,,点在的延长线上,,连接.
(1)求的长;
(2)动点从点出发,向终点运动,速度为2个单位/秒,运动时间为秒.
①当为何值时,;
②当为何值时,是以为腰的等腰三角形?
4.如图,已知△ABC中,AC=6cm,BC=8cm,AB=10cm,动点P从点C出发,沿着△ABC的三条边逆时针走一圈回到C点,速度为2cm/s,设运动时间为t秒.
(1)判断△ABC的形状,并求AB边上的高;
(2)t为何值时,△ACP为等腰三角形?
(3)另有一点Q,从点C开始,按顺时针走一圈回到C点,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
5.如图,△中,,若动点从点开始,按的路径运动,且速度为每秒,设运动的时间为秒。
(1)当为何值时,把△的周长分成相等的两部分。
(2)当为何值时,把△的面积分成相等的两部分,并求出此时的长;
(3)当为何值时,△为等腰三角形?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
