2020年秋人教版八年级数学上册随课练—12.3角的平分线的性质随堂练习(word版含答案 )
文档属性
| 名称 | 2020年秋人教版八年级数学上册随课练—12.3角的平分线的性质随堂练习(word版含答案 ) |

|
|
| 格式 | zip | ||
| 文件大小 | 176.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览


文档简介
12.3角的平分线的性质随堂练习
一、选择题
1.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A.有且只有1个
B.有且只有2个
C.组成∠E的角平分线
D.组成∠E的角平分线所在的直线(E点除外)
2.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为( )
A.3 B.5 C.6 D.不能确定
3.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;⑤S△ABD:S△ACD=AB:AC,其中正确的有(??
)
A.?5个???????????????????????????????????????B.?4个???????????????????????????????????????
C.?3个???????????????????????????????????????D.?2个
4.过线段AB外一点C,用直尺和圆规作AB的垂线段CD,以下四个作图中,作法错误的是(
??)
5.下列结论中,错误的是(
)
A.到已知角两边距离相等的点都在同一条直线上
B.一条直线上有一点到已知角的两边距离相等,这条直线平分已知角
C.到角的两边距离相等的点,与角顶点的连线平分这个角
D.角内有两点各自到角的两边的距离相等,经过这两点的直线平分这个角
6.已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为(
)
A.18
B.16
C.14
D.12
7.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=,PC=,AB=,AC=,则与的大小关系是(
)
A.>
B.<
C.=
D.无法确定
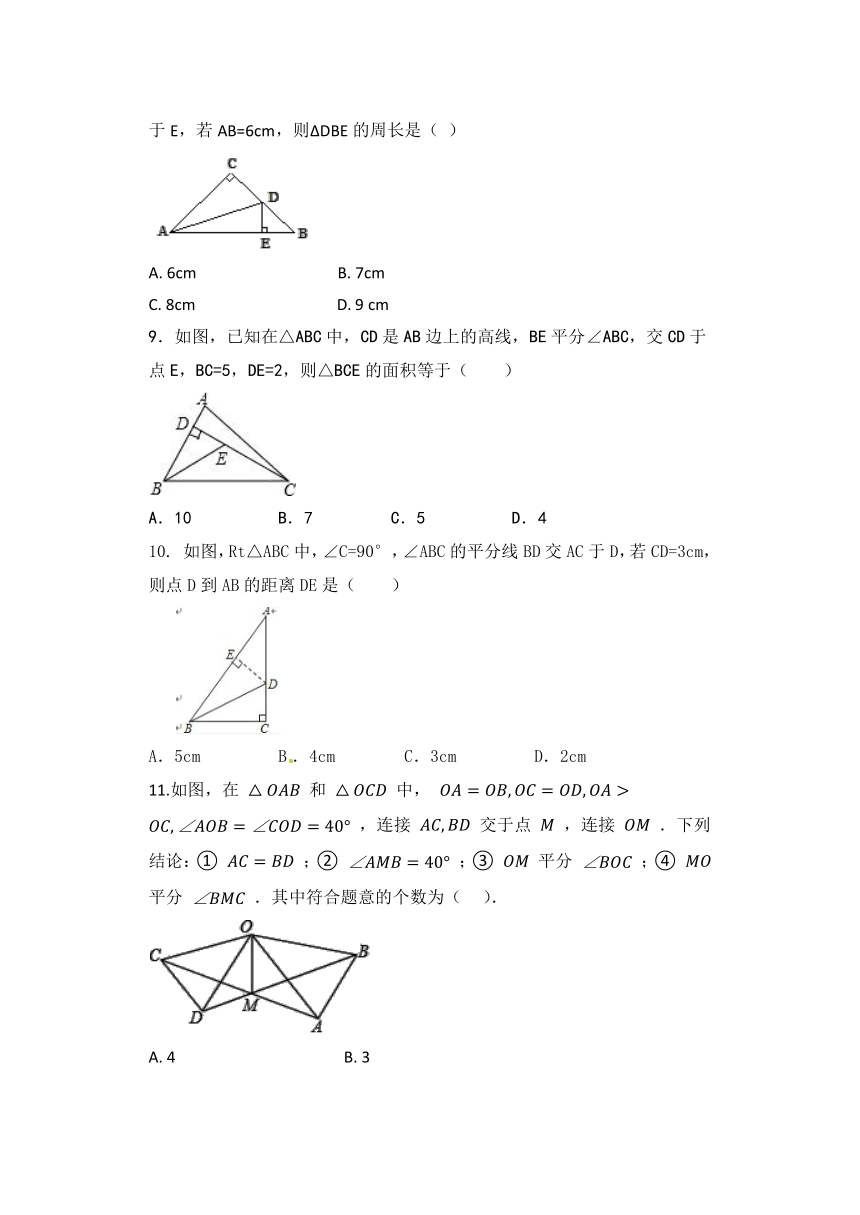
8.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则ΔDBE的周长是(
)
A.?6cm????????????????????????????????????B.?7cm????????????????????????????????????
C.?8cm????????????????????????????????????D.?9
cm
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10
B.7
C.5
D.4
10.
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
A.5cm
B.4cm
C.3cm
D.2cm
11.如图,在
和
中,
,连接
交于点
,连接
.下列结论:①
;②
;③
平分
;④
平分
.其中符合题意的个数为(???
).
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????
C.?2???????????????????????????????????????????D.?1
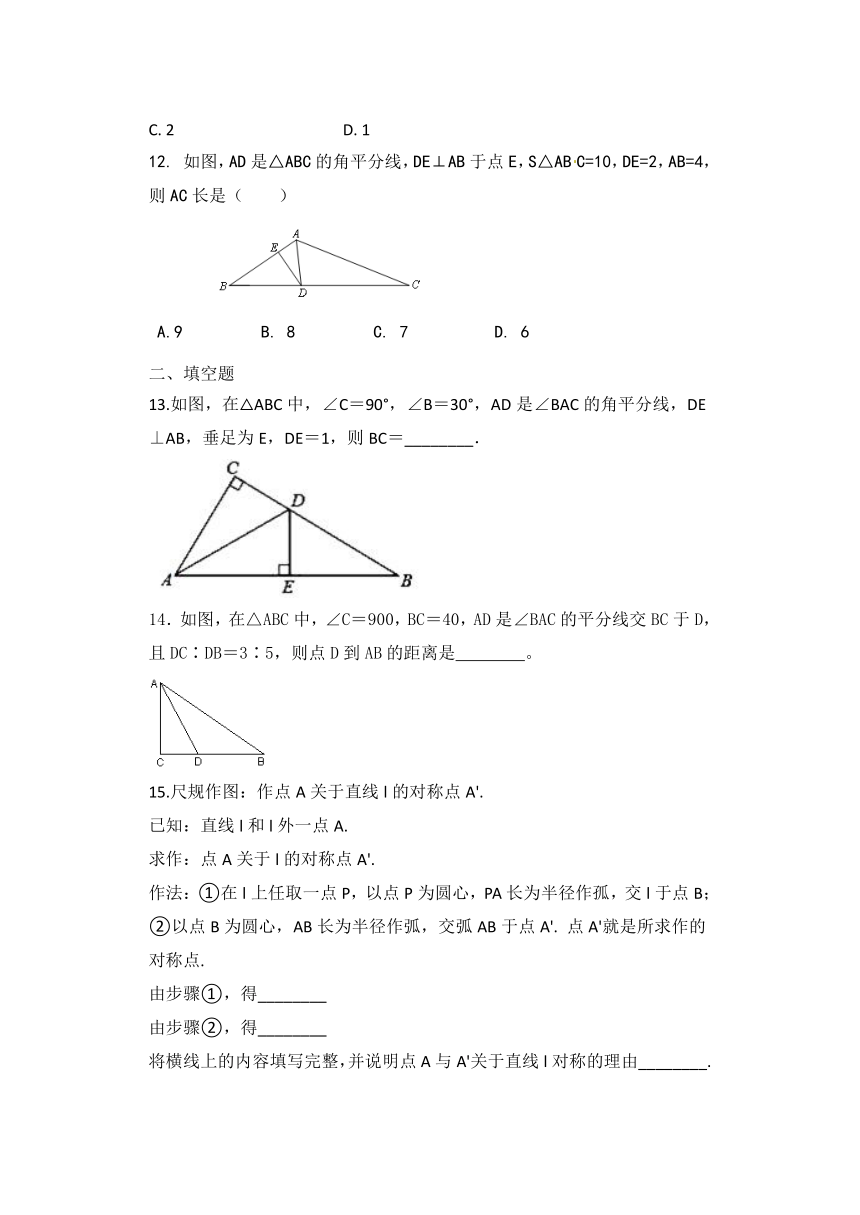
12.
如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=4,
则AC长是( )
A.9
B.
8
C.
7
D.
6
二、填空题
13.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=________.
14.如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是
。
15.尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'.
点A'就是所求作的对称点.
由步骤①,得________
由步骤②,得________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由________.
16.如图,AD是△ABC的角平分线,若AB=2AC.则S△ABD:S△ACD=______.
17.如图,△ABC中,∠C=90°,∠A=36°,DE⊥AB于D,且EC=ED,
∠EBC=
18.
如图,在△ABC中,∠ACB=90°,AD平分∠ABC,BC=10cm,BD:DC=3:2,则点D到AB的距离为
cm.
三、解答题
19.如图,AB=AC,BD=CD,DE⊥AB,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.
20.如图,DE∥BC,DF、BE分别平分∠ADE、∠ABC,求证:∠FDE=∠DEB。
21.如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
答案
1.
D
2.
C
3.
A
4.
B
5.
B
6.
C
7.
A
8.
A
9.
C
10.
C
11.
B
12.
D
13.
3
14.
15;
15.
PA=PB
;AB=BA'
;根据线段相等,即可证明三角形全等,证明对称
16.
2
17.
27
18.
4
19.
证明 在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∵DE⊥AB,DF⊥AC,∴DE=DF.
20.
证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
∠ADE,∠ABE=
∠ABC,
∴∠ADF=∠ABE
∴DF∥BE,
∴∠FDE=∠DEB
21.
解:(1)连接AO,OB,OC
∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,
∴OR=OQ,OR=OP,
∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,
∴AR=AQ,
同理BR=BP,CQ=CP,
即O在∠ACB角平分线上,
设BP=BR=x,CP=CQ=y,AQ=AR=z,
则
x=3,y=5,z=4,
∴BP=3,CQ=5,AR=4.
(2)过O作OM⊥AC于M,ON⊥AB于N
∵O在∠A的平分线,
∴OM=ON,∠ANO=∠AMO=90°,
∵∠A=60°,
∴∠NOM=120°,
∵O在∠ACB、∠ABC的角平分线上,
∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,
∴∠FON=∠EOM,
在△FON和△EOM中
∴△FON≌△EOM,
∴OE=OF.
一、选择题
1.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A.有且只有1个
B.有且只有2个
C.组成∠E的角平分线
D.组成∠E的角平分线所在的直线(E点除外)
2.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为( )
A.3 B.5 C.6 D.不能确定
3.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;⑤S△ABD:S△ACD=AB:AC,其中正确的有(??
)
A.?5个???????????????????????????????????????B.?4个???????????????????????????????????????
C.?3个???????????????????????????????????????D.?2个
4.过线段AB外一点C,用直尺和圆规作AB的垂线段CD,以下四个作图中,作法错误的是(
??)
5.下列结论中,错误的是(
)
A.到已知角两边距离相等的点都在同一条直线上
B.一条直线上有一点到已知角的两边距离相等,这条直线平分已知角
C.到角的两边距离相等的点,与角顶点的连线平分这个角
D.角内有两点各自到角的两边的距离相等,经过这两点的直线平分这个角
6.已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为(
)
A.18
B.16
C.14
D.12
7.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=,PC=,AB=,AC=,则与的大小关系是(
)
A.>
B.<
C.=
D.无法确定
8.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则ΔDBE的周长是(
)
A.?6cm????????????????????????????????????B.?7cm????????????????????????????????????
C.?8cm????????????????????????????????????D.?9
cm
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10
B.7
C.5
D.4
10.
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
A.5cm
B.4cm
C.3cm
D.2cm
11.如图,在
和
中,
,连接
交于点
,连接
.下列结论:①
;②
;③
平分
;④
平分
.其中符合题意的个数为(???
).
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????
C.?2???????????????????????????????????????????D.?1
12.
如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=4,
则AC长是( )
A.9
B.
8
C.
7
D.
6
二、填空题
13.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=________.
14.如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是
。
15.尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'.
点A'就是所求作的对称点.
由步骤①,得________
由步骤②,得________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由________.
16.如图,AD是△ABC的角平分线,若AB=2AC.则S△ABD:S△ACD=______.
17.如图,△ABC中,∠C=90°,∠A=36°,DE⊥AB于D,且EC=ED,
∠EBC=
18.
如图,在△ABC中,∠ACB=90°,AD平分∠ABC,BC=10cm,BD:DC=3:2,则点D到AB的距离为
cm.
三、解答题
19.如图,AB=AC,BD=CD,DE⊥AB,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.
20.如图,DE∥BC,DF、BE分别平分∠ADE、∠ABC,求证:∠FDE=∠DEB。
21.如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
答案
1.
D
2.
C
3.
A
4.
B
5.
B
6.
C
7.
A
8.
A
9.
C
10.
C
11.
B
12.
D
13.
3
14.
15;
15.
PA=PB
;AB=BA'
;根据线段相等,即可证明三角形全等,证明对称
16.
2
17.
27
18.
4
19.
证明 在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∵DE⊥AB,DF⊥AC,∴DE=DF.
20.
证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
∠ADE,∠ABE=
∠ABC,
∴∠ADF=∠ABE
∴DF∥BE,
∴∠FDE=∠DEB
21.
解:(1)连接AO,OB,OC
∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,
∴OR=OQ,OR=OP,
∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,
∴AR=AQ,
同理BR=BP,CQ=CP,
即O在∠ACB角平分线上,
设BP=BR=x,CP=CQ=y,AQ=AR=z,
则
x=3,y=5,z=4,
∴BP=3,CQ=5,AR=4.
(2)过O作OM⊥AC于M,ON⊥AB于N
∵O在∠A的平分线,
∴OM=ON,∠ANO=∠AMO=90°,
∵∠A=60°,
∴∠NOM=120°,
∵O在∠ACB、∠ABC的角平分线上,
∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,
∴∠FON=∠EOM,
在△FON和△EOM中
∴△FON≌△EOM,
∴OE=OF.
