北师大版九年级上册 数学 课件: 4.4探索三角形相似的条件(二)(共17张PPT)
文档属性
| 名称 | 北师大版九年级上册 数学 课件: 4.4探索三角形相似的条件(二)(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:45:20 | ||
图片预览



文档简介
(共17张PPT)
4.4探索三角形相似的条件(二)
(一)教学知识点
1.掌握三角形相似的判定方法2
2.会用相似三角形的判定方法2来判断、证明及计算.
(二)能力训练要求
通过自己动手并总结推出相似三角形的判定方法2,
培养学生的动手操作能力,总结概括能力.
(三)情感与价值观要求
1.通过探索相似三角形的判定方法2,体现数学活动充
满着探索性和创造性.
2.体会实践是检验真理的唯一标准
教学目标:
回顾
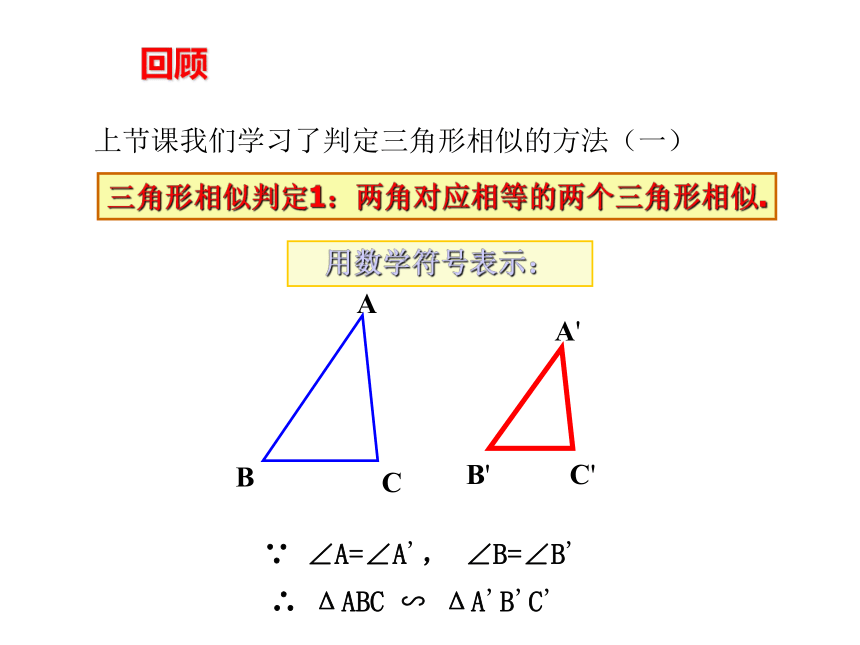
上节课我们学习了判定三角形相似的方法(一)
三角形相似判定1:两角对应相等的两个三角形相似.
用数学符号表示:
A
B
C
A'
C'
B'
∵
∠A=∠A',
∠B=∠B'
∴
ΔABC
∽
ΔA'B'C'
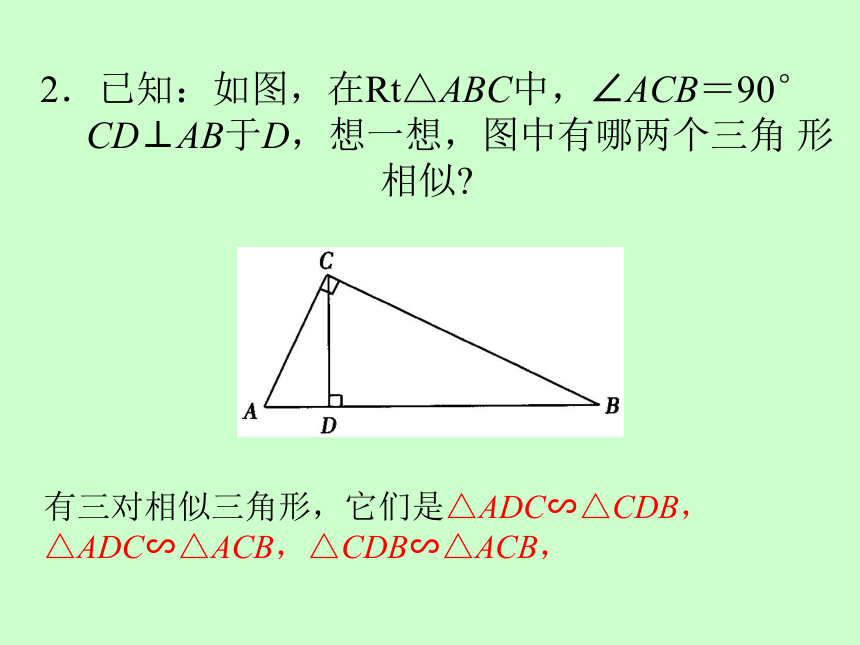
2.已知:如图,在Rt△ABC中,∠ACB=90°
CD⊥AB于D,想一想,图中有哪两个三角
形
相似?
有三对相似三角形,它们是△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB,
探索三角形系相似的条件
如果△ABC与
有两边对应成比例
那么这两个三角形相似吗?
探究一
K=2
观察下图
实践是检验真理的唯一标准
14cm
20cm
A
B
C
7cm
10cm
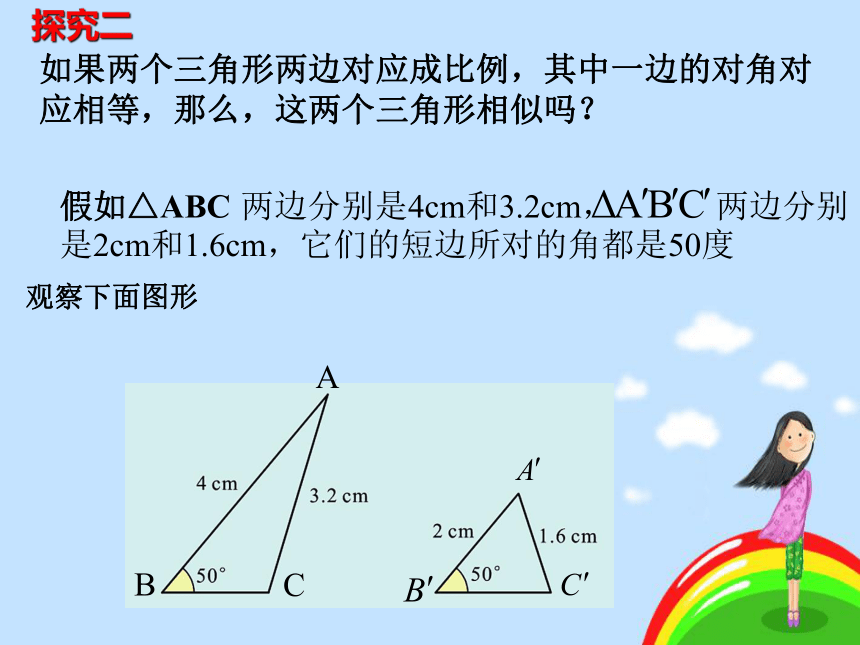
探究二
观察下面图形
如果两个三角形两边对应成比例,其中一边的对角对应相等,那么,这两个三角形相似吗?
假如△ABC
两边分别是4cm和3.2cm,
两边分别
是2cm和1.6cm,它们的短边所对的角都是50度
A
B
C
演示
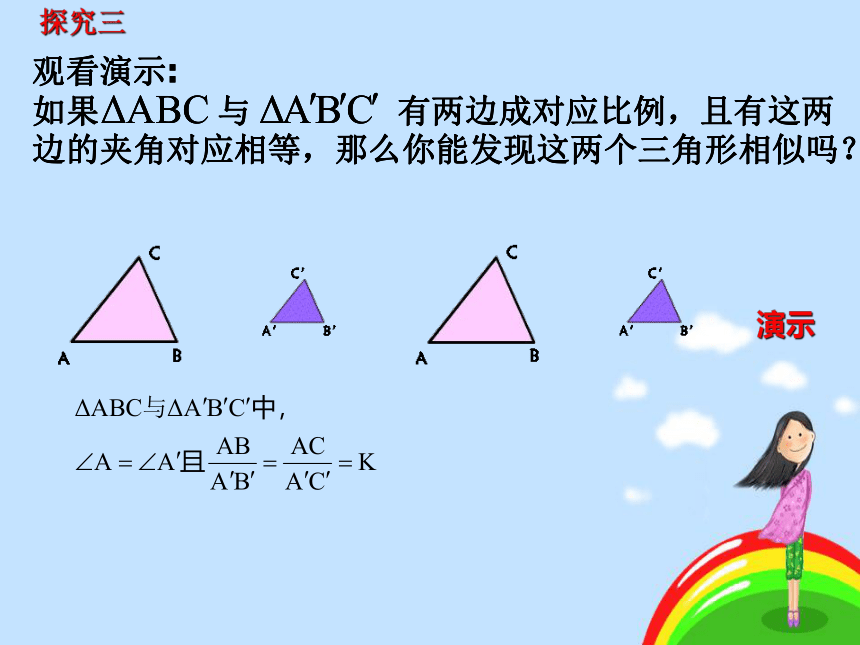
探究三
观看演示:
如果
与
有两边成对应比例,且有这两
边的夹角对应相等,那么你能发现这两个三角形相似吗?
观看演示:
如果
与
有两边成对应比例,且有这两
边的夹角对应相等,那么你能发现这两个三角形相似吗?
A
B
C
C'
B'
A'
6
cm
4
cm
3
cm
2
cm
两边对应成比例且夹角相等
△A
'
B
'
C
'
∽△ABC
∠B
'
=∠B
例证
△A
'
B
'
C
'
∽△ABC
∠B’=∠B
∠B’=∠B
∵
△A’B’C’
∽△ABC
∴
三角形相似判定2:两边对应成比例且夹角
对应相等,两三角形相似.
几何语言:
特别提示:两边对应成比例并且必须是夹角
对应相等的两三角形才相似哦.
例1
判断图中△AEB和△FEC是否相似?
解
:相似
,
∵∠AEB=∠FEC(对应角相等)
?
又∵
=
=1.5
?
=
=1.5
?
∴
=
?
∴
△AEB∽△FEC
例2
如图,D在△
ABC的AB边上,AD=1,BD=2,
AC=
,问△
ACD与△
ABC相似吗?
请说明你的理由.
想一想
当堂达标:
1、下列条件能判定△ABC∽△A′B′C′的有(
)
(1)∠A=45°,AB=12,AC=15,∠A′=
45°
,A′B′=16,A′C′=20
(2)∠A=47°,AB=1,AC=2,∠B′=47°,A′B′=2,A′C′=4
(3)∠A=47°,AB=2,AC=3,∠B′=47°,A′B′=4,B′C′=6
A、0个
B、1个
C、2个
D、3个
2、如图,在△ABC中,D在AB上,要说明△ACD∽△ABC
相似,已经具备了条件
,还需添加的条件是
,或
或
.
A
C
D
B
B
∠
DAC=∠CAB
∠ADC=∠
ACB
∠
ACD=
∠
ABC
AD:AC=AC:AB
A
D
E
C
B
3、如图,已知
,
试求
的值;
4、如图,AB·AE=AD·AC,且∠1=∠2,求证:
△ABC∽△ADE
D
B
E
C
A
2
1
拓展提升:
自己来小结一下吧!
小结
一、两个三角形相似的判定方法:
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个
三角形相似.
二、判定两个三角形相似,要看条件、选对方法
家庭作业
?
课堂精炼:1、97、98页的训练案与加强案
2、预习下节内容
5、如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?为什么?
A
1
B
1
C
1
B
2
A
2
C
2
6、如图,在正方形ABCD中,点M、N分别在AB、BC上,
AB=4,AM=1,BN=0.75,(1)△ADM与△BMN相
似吗?为什么?(2)求∠DMN的度数;
D
A
M
B
N
C
课外延伸
4.4探索三角形相似的条件(二)
(一)教学知识点
1.掌握三角形相似的判定方法2
2.会用相似三角形的判定方法2来判断、证明及计算.
(二)能力训练要求
通过自己动手并总结推出相似三角形的判定方法2,
培养学生的动手操作能力,总结概括能力.
(三)情感与价值观要求
1.通过探索相似三角形的判定方法2,体现数学活动充
满着探索性和创造性.
2.体会实践是检验真理的唯一标准
教学目标:
回顾
上节课我们学习了判定三角形相似的方法(一)
三角形相似判定1:两角对应相等的两个三角形相似.
用数学符号表示:
A
B
C
A'
C'
B'
∵
∠A=∠A',
∠B=∠B'
∴
ΔABC
∽
ΔA'B'C'
2.已知:如图,在Rt△ABC中,∠ACB=90°
CD⊥AB于D,想一想,图中有哪两个三角
形
相似?
有三对相似三角形,它们是△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB,
探索三角形系相似的条件
如果△ABC与
有两边对应成比例
那么这两个三角形相似吗?
探究一
K=2
观察下图
实践是检验真理的唯一标准
14cm
20cm
A
B
C
7cm
10cm
探究二
观察下面图形
如果两个三角形两边对应成比例,其中一边的对角对应相等,那么,这两个三角形相似吗?
假如△ABC
两边分别是4cm和3.2cm,
两边分别
是2cm和1.6cm,它们的短边所对的角都是50度
A
B
C
演示
探究三
观看演示:
如果
与
有两边成对应比例,且有这两
边的夹角对应相等,那么你能发现这两个三角形相似吗?
观看演示:
如果
与
有两边成对应比例,且有这两
边的夹角对应相等,那么你能发现这两个三角形相似吗?
A
B
C
C'
B'
A'
6
cm
4
cm
3
cm
2
cm
两边对应成比例且夹角相等
△A
'
B
'
C
'
∽△ABC
∠B
'
=∠B
例证
△A
'
B
'
C
'
∽△ABC
∠B’=∠B
∠B’=∠B
∵
△A’B’C’
∽△ABC
∴
三角形相似判定2:两边对应成比例且夹角
对应相等,两三角形相似.
几何语言:
特别提示:两边对应成比例并且必须是夹角
对应相等的两三角形才相似哦.
例1
判断图中△AEB和△FEC是否相似?
解
:相似
,
∵∠AEB=∠FEC(对应角相等)
?
又∵
=
=1.5
?
=
=1.5
?
∴
=
?
∴
△AEB∽△FEC
例2
如图,D在△
ABC的AB边上,AD=1,BD=2,
AC=
,问△
ACD与△
ABC相似吗?
请说明你的理由.
想一想
当堂达标:
1、下列条件能判定△ABC∽△A′B′C′的有(
)
(1)∠A=45°,AB=12,AC=15,∠A′=
45°
,A′B′=16,A′C′=20
(2)∠A=47°,AB=1,AC=2,∠B′=47°,A′B′=2,A′C′=4
(3)∠A=47°,AB=2,AC=3,∠B′=47°,A′B′=4,B′C′=6
A、0个
B、1个
C、2个
D、3个
2、如图,在△ABC中,D在AB上,要说明△ACD∽△ABC
相似,已经具备了条件
,还需添加的条件是
,或
或
.
A
C
D
B
B
∠
DAC=∠CAB
∠ADC=∠
ACB
∠
ACD=
∠
ABC
AD:AC=AC:AB
A
D
E
C
B
3、如图,已知
,
试求
的值;
4、如图,AB·AE=AD·AC,且∠1=∠2,求证:
△ABC∽△ADE
D
B
E
C
A
2
1
拓展提升:
自己来小结一下吧!
小结
一、两个三角形相似的判定方法:
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个
三角形相似.
二、判定两个三角形相似,要看条件、选对方法
家庭作业
?
课堂精炼:1、97、98页的训练案与加强案
2、预习下节内容
5、如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?为什么?
A
1
B
1
C
1
B
2
A
2
C
2
6、如图,在正方形ABCD中,点M、N分别在AB、BC上,
AB=4,AM=1,BN=0.75,(1)△ADM与△BMN相
似吗?为什么?(2)求∠DMN的度数;
D
A
M
B
N
C
课外延伸
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
