初中数学人教版八年级上册13.3.1 等腰三角形 同步练习(Word版含答案)
文档属性
| 名称 | 初中数学人教版八年级上册13.3.1 等腰三角形 同步练习(Word版含答案) | 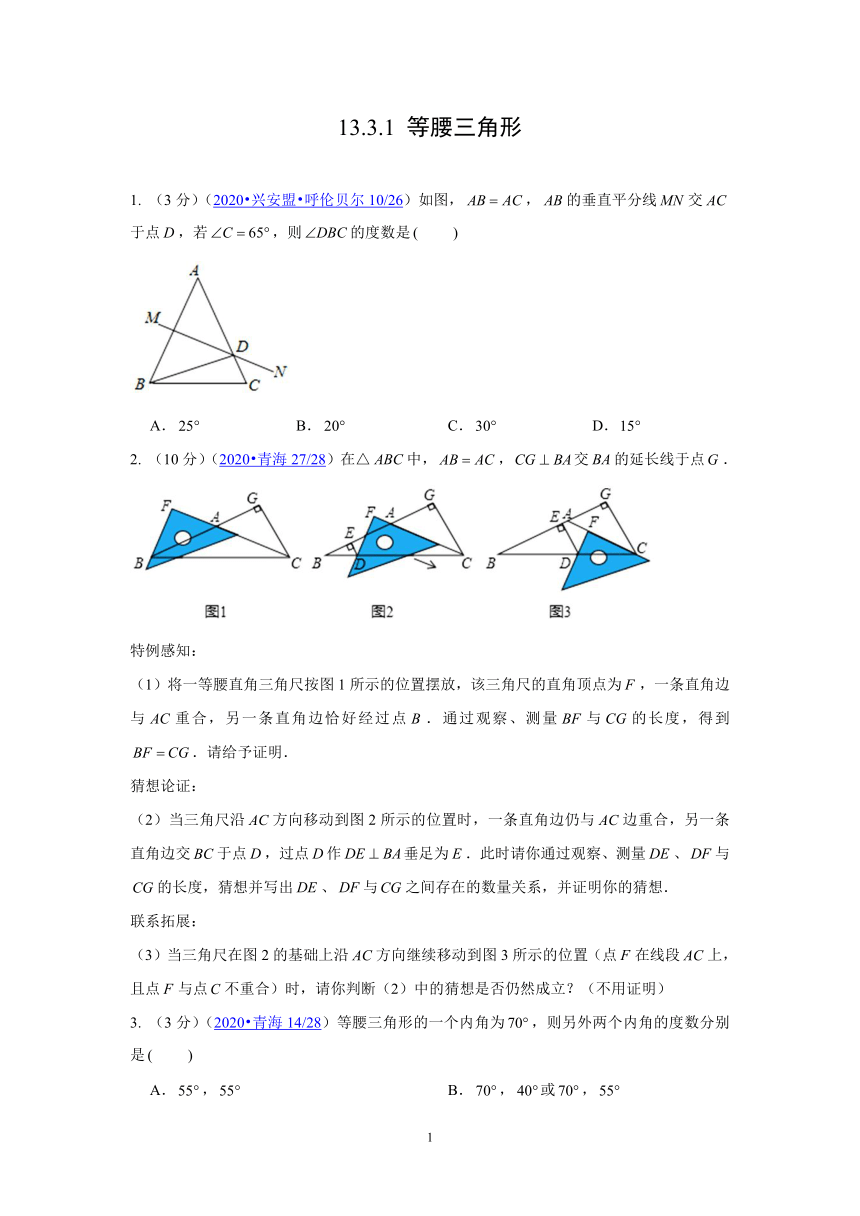 | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 16:03:33 | ||
图片预览




文档简介
13.3.1 等腰三角形
1. (3分)(\l "答案2020兴安盟呼伦贝尔1026" 2020?兴安盟?呼伦贝尔10/26)如图,,的垂直平分线交于点,若,则的度数是
A. B. C. D.
2. (10分)(\l "答案2020青海2728" 2020?青海27/28)在△中,,交的延长线于点.
特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为,一条直角边与重合,另一条直角边恰好经过点.通过观察、测量与的长度,得到.请给予证明.
猜想论证:
(2)当三角尺沿方向移动到图2所示的位置时,一条直角边仍与边重合,另一条直角边交于点,过点作垂足为.此时请你通过观察、测量、与的长度,猜想并写出、与之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿方向继续移动到图3所示的位置(点在线段上,且点与点不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
3. (3分)(\l "答案2020青海1428" 2020?青海14/28)等腰三角形的一个内角为,则另外两个内角的度数分别是
A., B.,或,
C., D.,或,
4. (2分)(\l "答案2020青海0728" 2020?青海7/28)已知,,为△的三边长.,满足,且为方程的解,则△的形状为 三角形.
5. (6分)(\l "答案2020广东2025" 2020?广东20/25)如图,在△中,点,分别是、边上的点,,,与相交于点.求证:△是等腰三角形.
6. (4分)(\l "答案2020福建0525" 2020?福建5/25)如图,是等腰三角形的顶角平分线,,则等于
A.10 B.5 C.4 D.3
7. (2分)(\l "答案2020北京1428" 2020?北京14/28)如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是 (写出一个即可).
8. (10分)(\l "答案2019重庆2026" 2019·重庆市20/26)如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
9. (3分)(\l "答案2018包头0826" 2018·包头8/26)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
10. (3分)(\l "答案2016北京1429" 2016?北京14/29) 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m, 已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高
为 m.
11.(3分)(\l "答案2015黄石0825" 2015?黄石8/25)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B.54° C.18° D.64°
12. (3分)(\l "答案2015盐城0728" 2015?盐城7/28)若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A. 12 B. 9 C. 12或9 D. 9或7
13. (3分)(\l "答案2015鄂尔多斯0924" 2015?鄂尔多斯9/24)下列说法中,正确的有( )
①等腰三角形两边长为2和5,则它的周长是9或12
②无理数 在-2和1之间
③六边形的内角和是外角和的2倍
④若a>b,则a-b>0.它的逆命题是假命题
⑤北偏东30°与南偏东50°的两条射线组成的角为80°
A.1个 B.2个 C.3个 D.4个
14. (3分)(\l "答案2015陕西0626" 2015?陕西6/26)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
15. (3分)(\l "答案2015鄂尔多斯1624" 2015?鄂尔多斯16/24)如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG, 垂足为G,MG与BC相交于点H,若MH =8 cm,则BG = cm.
16. (3分)(\l "答案2014扬州1028" 2014?扬州10/28)若等腰三角形的两条边长分别为7 cm和14 cm,则它的周长为 cm.
解 析
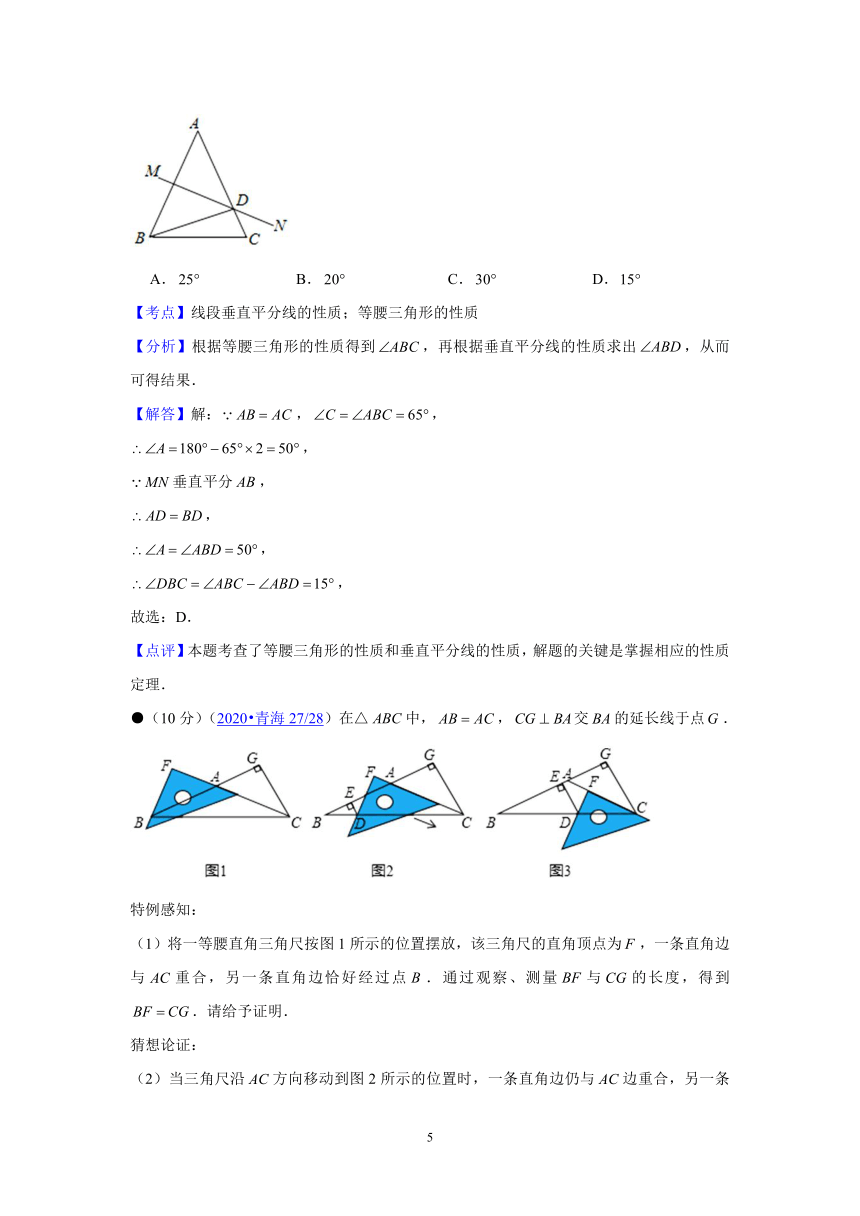
●(3分)(\l "原题2020兴安盟呼伦贝尔1026" 2020?兴安盟?呼伦贝尔10/26)如图,,的垂直平分线交于点,若,则的度数是
A. B. C. D.
【考点】线段垂直平分线的性质;等腰三角形的性质
【分析】根据等腰三角形的性质得到,再根据垂直平分线的性质求出,从而可得结果.
【解答】解:,,
,
垂直平分,
,
,
,
故选:D.
【点评】本题考查了等腰三角形的性质和垂直平分线的性质,解题的关键是掌握相应的性质定理.
●(10分)(\l "原题2020青海2728" 2020?青海27/28)在△中,,交的延长线于点.
特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为,一条直角边与重合,另一条直角边恰好经过点.通过观察、测量与的长度,得到.请给予证明.
猜想论证:
(2)当三角尺沿方向移动到图2所示的位置时,一条直角边仍与边重合,另一条直角边交于点,过点作垂足为.此时请你通过观察、测量、与的长度,猜想并写出、与之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿方向继续移动到图3所示的位置(点在线段上,且点与点不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
【考点】三角形综合题
【分析】(1)证明△FAB≌△GAC即可解决问题.
(2)结论:.利用面积法证明即可.
(3)结论不变,证明方法类似(2).
【解答】(1)证明:如图1中,
,,,
∴△FAB≌△GAC(AAS),
.
(2)解:结论:.
理由:如图2中,连接.
,,,,
,
,
.
(3)解:结论不变:.
理由:如图3中,连接.
,,,,
,
,
.
【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,三角形的面积等知识,解题的关键是学会利用面积法证明线段之间的关系,属于中考常考题型.
●(3分)(\l "原题2020青海1428" 2020?青海14/28)等腰三角形的一个内角为,则另外两个内角的度数分别是
A., B.,或,
C., D.,或,
【考点】等腰三角形的性质
【分析】已知给出了一个内角是,没有明确是顶角还是底角,所以要进行分类讨论,分类后还需用三角形内角和定理去验证每种情况是不是都成立.
【解答】解:分情况讨论:
(1)若等腰三角形的顶角为时,底角;
(2)若等腰三角形的底角为时,它的另外一个底角为,顶角为.
故选:D.
【点评】本题考查了等腰三角形的性质及三角形的内角和定理;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.
●(2分)(\l "原题2020青海0728" 2020?青海7/28)已知,,为△的三边长.,满足,且为方程的解,则△的形状为 等腰 三角形.
【考点】等腰三角形的判定;含绝对值符号的一元一次方程;非负数的性质:偶次方;非负数的性质:绝对值
【分析】利用绝对值的性质以及偶次方的性质得出,的值,进而利用三角形三边关系得出的值,进而判断出其形状.
【解答】解:,
,,
解得:,,
为方程的解,
,
解得:或2,
、、为△的三边长,,
不合题意,舍去,
,
,
∴△是等腰三角形,
故答案为:等腰.
【点评】此题主要考查了等腰三角形的判定,三角形三边关系以及绝对值的性质和偶次方的性质,得出的值是解题关键.
●(6分)(\l "原题2020广东2025" 2020?广东20/25)如图,在△中,点,分别是、边上的点,,,与相交于点.求证:△是等腰三角形.
【考点】全等三角形的判定与性质;等腰三角形的判定
【分析】先证△≌△(AAS),得出,,则,再证△≌△(AAS),得出即可.
【解答】证明:,
,
在△和△中,,
∴△≌△(AAS),
,,
,
即,
在△和△中,,
∴△≌△(AAS),
,
∴△是等腰三角形.
【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定;证明三角形全等是解题的关键.
●(4分)(\l "原题2020福建0525" 2020?福建5/25)如图,是等腰三角形的顶角平分线,,则等于
A.10 B.5 C.4 D.3
【考点】等腰三角形的性质
【分析】根据等腰三角形三线合一的性质即可求解.
【解答】解:是等腰三角形的顶角平分线,,
.
故选:B.
【点评】考查了等腰三角形的性质,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
●(2分)(\l "原题2020北京1428" 2020?北京14/28)如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是 BD=CD (写出一个即可).
【考点】全等三角形的判定;等腰三角形的性质.有
【答案】见试题解答内容
【分析】由题意可得∠ABC=∠ACD,AB=AC,即添加一组边对应相等,可证△ABD与△ACD全等.
【解答】解:∵AB=AC,
∴∠ABD=∠ACD,
添加BD=CD,
∴在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
故答案为:BD=CD.
【点评】本题考查了全等三角形的判定,灵活运用全等三角形的判定是本题的关键.
●(10分)(\l "原题2019重庆2026" 2019·重庆市20/26)如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
【考点】平行线的性质;等腰三角形的性质.
【分析】(1)利用等腰三角形的三线合一的性质证明∠ADB=90°,再利用等腰三角形的性质求出∠ABC即可解决问题.
(2)只要证明∠FBE=∠FEB即可解决问题.
【解答】(1)解:∵AB=AC,
∴∠C=∠ABC,
∵∠C=36°,
∴∠ABC=36°,
∵BD=CD,AB=AC,
∴AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣36°=54°.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC,
∵EF∥BC,
∴∠FEB=∠CBE,
∴∠FBE=∠FEB,
∴FB=FE.
【点评】本题考查等腰三角形的性质,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
●(3分)(\l "原题2018包头0826" 2018·包头8/26)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
【考点】等腰直角三角形.有
【分析】由AB=AC知∠B=∠C,据此得2∠C+∠BAC=180°,结合∠C+∠BAC=145°可知∠C=35°,根据∠DAE=90°、AD=AE知∠AED=45°,利用∠EDC=∠AED﹣∠C可得答案.
【解答】解:∵AB=AC,
∴∠B=∠C,
∴∠B+∠C+∠BAC=2∠C+∠BAC=180°,
又∵∠C+∠BAC=145°,
∴∠C=35°,
∵∠DAE=90°,AD=AE,
∴∠AED=45°,
∴∠EDC=∠AED﹣∠C=10°,
故选:D.
【点评】本题主要考查等腰直角三角形,解题的关键是掌握等腰直角三角形和等腰三角形的性质及三角形的内角和定理、外角的性质.
●(3分)(\l "原题2016北京1429" 2016?北京14/29) 如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m, 已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为 m.
答案:3
考点:等腰直角三角形判定与性质.
解析:方法一:
如下图,因为小军、小珠都身高与影长相等,所以,
∠E=∠F=45°,所以,AB=BE=BF,设路灯的高AB为 x m,
则BD=x-1.5,BC=x-1.8,
又CD=2.7,所以,x-1.5+x-1.8=2.7,解得:x=3(m).
方法二:
如图:
∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,,
即:,,
解得:AB=3 m,
答:路灯的高为3 m.
【分析】根据CD∥AB∥MN,得到△ABE∽△CDE,△ABF∽△MNF,根据相似三角形的性质得到,,即可得到结论.本题考查了中心投影,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.
●(3分)(\l "原题2015黄石0825" 2015?黄石8/25)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B.54° C.18° D.64°
【考点】等腰三角形的性质.
【分析】根据等腰三角形的性质由已知可求得∠A的度数,再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数.
【解答】解:∵AB=AC,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴∠A=36°,
∵BD⊥AC,
∴∠ABD=90°﹣36°=54°.
故选:B.
【点评】本题主要考查等腰三角形的性质,解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题,此题难度一般.
●(3分)(\l "原题2015盐城0728" 2015?盐城7/28)若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A. 12 B. 9 C. 12或9 D. 9或7
考点: 等腰三角形的性质;三角形三边关系.
分析: 利用等腰三角形的性质以及三角形三边关系得出其周长即可.
解答:解:∵一个等腰三角形的两边长分别是2和5,
∴当腰长为2,则2+2<5,此时不成立,
当腰长为5时,则它的周长为:5+5+2=12.
故选:A.
点评: 此题主要考查了等腰三角形的性质以及三角形三边关系,正确分类讨论得出是解题关键.
●(3分)(\l "原题2015鄂尔多斯0924" 2015?鄂尔多斯9/24)下列说法中,正确的有( )
①等腰三角形两边长为2和5,则它的周长是9或12
②无理数 在-2和1之间
③六边形的内角和是外角和的2倍
④若a>b,则a-b>0.它的逆命题是假命题
⑤北偏东30°与南偏东50°的两条射线组成的角为80°
A.1个 B.2个 C.3个 D.4个
【考点】命题与定理
【分析】①利用等腰三角形的性质以及三角形三边关系得出其周长即可.
②利用“夹逼法”计算.
③六边形的内角和是外角和的2倍.
④根据不等式的性质进行判断.
⑤根据方位角的概念和平角的定义解答.
【解答】解:①一个等腰三角形的两边长分别是2和5,
当腰长为2,则,此时不成立,
当腰长为5时,则它的周长为:.
即该三角形的周长是12.
故①错误;
②无理数在和之间.故②正确;
③,即六边形的内角和是外角和的2倍.故③正确;
④若,则.它的逆命题是真命题,故④错误;
⑤北偏东与南偏东的两条射线组成的角为.故⑤错误.
故选:B.
【点评】本题考查了命题.需要掌握不等式的性质,命题与逆命题,等腰三角形的性质以及无理数的大小比较,属于基础题.
●(3分)(\l "原题2015鄂尔多斯1624" 2015?鄂尔多斯16/24)如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG, 垂足为G,MG与BC相交于点H,若MH =8 cm,则BG = cm.
【考点】全等三角形的判定与性质;等腰直角三角形
【分析】如图,作于,延长交的延长线于,构建等腰△、全等三角形△和△,利用等腰三角形的性质和全等三角形的对应边相等得到:,所以.
【解答】解:如图,作于,延长交的延长线于,
∵△中,,,
,
,
,
,
,
,
.
∵MD∥AC,
,
∴△为等腰直角三角形
,
而,
平分,
而,
,即,
,
,
,,
,
在△和△中,
,
∴△≌△(AAS),
,
.
故答案是:4.
【点评】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.
●(3分)(\l "原题2015陕西0626" 2015?陕西6/26)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
【考点】等腰三角形的判定与性质.
【分析】根据已知条件分别求出图中三角形的内角度数,再根据等腰三角形的判定即可找出图中的等腰三角形.
【解答】解:∵AB=AC,
∴△ABC是等腰三角形;
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC=∠ABC=36°,
∴∠A=∠ABD=36°,
∴BD=AD,
∴△ABD是等腰三角形;
在△BCD中,∵∠BDC=180°﹣∠DBC﹣∠C=180°﹣36°﹣72°=72°,
∴∠C=∠BDC=72°,
∴BD=BC,
∴△BCD是等腰三角形;
∵BE=BC,
∴BD=BE,
∴△BDE是等腰三角形;
∴∠BED=(180°﹣36°)÷2=72°,
∴∠ADE=∠BED﹣∠A=72°﹣36°=36°,
∴∠A=∠ADE,
∴DE=AE,
∴△ADE是等腰三角形;
∴图中的等腰三角形有5个.
故选D.
【点评】此题考查了等腰三角形的判定,用到的知识点是等腰三角形的判定、三角形内角和定理、三角形外角的性质、三角形的角平分线定义等,解题时要找出所有的等腰三角形,不要遗漏.
●(3分)(\l "原题2014扬州1028" 2014?扬州10/28)若等腰三角形的两条边长分别为7 cm和14 cm,则它的周长为 cm.
【解答】解:①14cm为腰,7cm为底,此时周长为14+14+7=35cm;
②14cm为底,7cm为腰,则两边和等于第三边无法构成三角形,故舍去.
故其周长是35cm.
故答案为:35.
18
1. (3分)(\l "答案2020兴安盟呼伦贝尔1026" 2020?兴安盟?呼伦贝尔10/26)如图,,的垂直平分线交于点,若,则的度数是
A. B. C. D.
2. (10分)(\l "答案2020青海2728" 2020?青海27/28)在△中,,交的延长线于点.
特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为,一条直角边与重合,另一条直角边恰好经过点.通过观察、测量与的长度,得到.请给予证明.
猜想论证:
(2)当三角尺沿方向移动到图2所示的位置时,一条直角边仍与边重合,另一条直角边交于点,过点作垂足为.此时请你通过观察、测量、与的长度,猜想并写出、与之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿方向继续移动到图3所示的位置(点在线段上,且点与点不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
3. (3分)(\l "答案2020青海1428" 2020?青海14/28)等腰三角形的一个内角为,则另外两个内角的度数分别是
A., B.,或,
C., D.,或,
4. (2分)(\l "答案2020青海0728" 2020?青海7/28)已知,,为△的三边长.,满足,且为方程的解,则△的形状为 三角形.
5. (6分)(\l "答案2020广东2025" 2020?广东20/25)如图,在△中,点,分别是、边上的点,,,与相交于点.求证:△是等腰三角形.
6. (4分)(\l "答案2020福建0525" 2020?福建5/25)如图,是等腰三角形的顶角平分线,,则等于
A.10 B.5 C.4 D.3
7. (2分)(\l "答案2020北京1428" 2020?北京14/28)如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是 (写出一个即可).
8. (10分)(\l "答案2019重庆2026" 2019·重庆市20/26)如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
9. (3分)(\l "答案2018包头0826" 2018·包头8/26)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
10. (3分)(\l "答案2016北京1429" 2016?北京14/29) 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m, 已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高
为 m.
11.(3分)(\l "答案2015黄石0825" 2015?黄石8/25)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B.54° C.18° D.64°
12. (3分)(\l "答案2015盐城0728" 2015?盐城7/28)若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A. 12 B. 9 C. 12或9 D. 9或7
13. (3分)(\l "答案2015鄂尔多斯0924" 2015?鄂尔多斯9/24)下列说法中,正确的有( )
①等腰三角形两边长为2和5,则它的周长是9或12
②无理数 在-2和1之间
③六边形的内角和是外角和的2倍
④若a>b,则a-b>0.它的逆命题是假命题
⑤北偏东30°与南偏东50°的两条射线组成的角为80°
A.1个 B.2个 C.3个 D.4个
14. (3分)(\l "答案2015陕西0626" 2015?陕西6/26)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
15. (3分)(\l "答案2015鄂尔多斯1624" 2015?鄂尔多斯16/24)如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG, 垂足为G,MG与BC相交于点H,若MH =8 cm,则BG = cm.
16. (3分)(\l "答案2014扬州1028" 2014?扬州10/28)若等腰三角形的两条边长分别为7 cm和14 cm,则它的周长为 cm.
解 析
●(3分)(\l "原题2020兴安盟呼伦贝尔1026" 2020?兴安盟?呼伦贝尔10/26)如图,,的垂直平分线交于点,若,则的度数是
A. B. C. D.
【考点】线段垂直平分线的性质;等腰三角形的性质
【分析】根据等腰三角形的性质得到,再根据垂直平分线的性质求出,从而可得结果.
【解答】解:,,
,
垂直平分,
,
,
,
故选:D.
【点评】本题考查了等腰三角形的性质和垂直平分线的性质,解题的关键是掌握相应的性质定理.
●(10分)(\l "原题2020青海2728" 2020?青海27/28)在△中,,交的延长线于点.
特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为,一条直角边与重合,另一条直角边恰好经过点.通过观察、测量与的长度,得到.请给予证明.
猜想论证:
(2)当三角尺沿方向移动到图2所示的位置时,一条直角边仍与边重合,另一条直角边交于点,过点作垂足为.此时请你通过观察、测量、与的长度,猜想并写出、与之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿方向继续移动到图3所示的位置(点在线段上,且点与点不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
【考点】三角形综合题
【分析】(1)证明△FAB≌△GAC即可解决问题.
(2)结论:.利用面积法证明即可.
(3)结论不变,证明方法类似(2).
【解答】(1)证明:如图1中,
,,,
∴△FAB≌△GAC(AAS),
.
(2)解:结论:.
理由:如图2中,连接.
,,,,
,
,
.
(3)解:结论不变:.
理由:如图3中,连接.
,,,,
,
,
.
【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,三角形的面积等知识,解题的关键是学会利用面积法证明线段之间的关系,属于中考常考题型.
●(3分)(\l "原题2020青海1428" 2020?青海14/28)等腰三角形的一个内角为,则另外两个内角的度数分别是
A., B.,或,
C., D.,或,
【考点】等腰三角形的性质
【分析】已知给出了一个内角是,没有明确是顶角还是底角,所以要进行分类讨论,分类后还需用三角形内角和定理去验证每种情况是不是都成立.
【解答】解:分情况讨论:
(1)若等腰三角形的顶角为时,底角;
(2)若等腰三角形的底角为时,它的另外一个底角为,顶角为.
故选:D.
【点评】本题考查了等腰三角形的性质及三角形的内角和定理;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.
●(2分)(\l "原题2020青海0728" 2020?青海7/28)已知,,为△的三边长.,满足,且为方程的解,则△的形状为 等腰 三角形.
【考点】等腰三角形的判定;含绝对值符号的一元一次方程;非负数的性质:偶次方;非负数的性质:绝对值
【分析】利用绝对值的性质以及偶次方的性质得出,的值,进而利用三角形三边关系得出的值,进而判断出其形状.
【解答】解:,
,,
解得:,,
为方程的解,
,
解得:或2,
、、为△的三边长,,
不合题意,舍去,
,
,
∴△是等腰三角形,
故答案为:等腰.
【点评】此题主要考查了等腰三角形的判定,三角形三边关系以及绝对值的性质和偶次方的性质,得出的值是解题关键.
●(6分)(\l "原题2020广东2025" 2020?广东20/25)如图,在△中,点,分别是、边上的点,,,与相交于点.求证:△是等腰三角形.
【考点】全等三角形的判定与性质;等腰三角形的判定
【分析】先证△≌△(AAS),得出,,则,再证△≌△(AAS),得出即可.
【解答】证明:,
,
在△和△中,,
∴△≌△(AAS),
,,
,
即,
在△和△中,,
∴△≌△(AAS),
,
∴△是等腰三角形.
【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定;证明三角形全等是解题的关键.
●(4分)(\l "原题2020福建0525" 2020?福建5/25)如图,是等腰三角形的顶角平分线,,则等于
A.10 B.5 C.4 D.3
【考点】等腰三角形的性质
【分析】根据等腰三角形三线合一的性质即可求解.
【解答】解:是等腰三角形的顶角平分线,,
.
故选:B.
【点评】考查了等腰三角形的性质,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
●(2分)(\l "原题2020北京1428" 2020?北京14/28)如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是 BD=CD (写出一个即可).
【考点】全等三角形的判定;等腰三角形的性质.有
【答案】见试题解答内容
【分析】由题意可得∠ABC=∠ACD,AB=AC,即添加一组边对应相等,可证△ABD与△ACD全等.
【解答】解:∵AB=AC,
∴∠ABD=∠ACD,
添加BD=CD,
∴在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
故答案为:BD=CD.
【点评】本题考查了全等三角形的判定,灵活运用全等三角形的判定是本题的关键.
●(10分)(\l "原题2019重庆2026" 2019·重庆市20/26)如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
【考点】平行线的性质;等腰三角形的性质.
【分析】(1)利用等腰三角形的三线合一的性质证明∠ADB=90°,再利用等腰三角形的性质求出∠ABC即可解决问题.
(2)只要证明∠FBE=∠FEB即可解决问题.
【解答】(1)解:∵AB=AC,
∴∠C=∠ABC,
∵∠C=36°,
∴∠ABC=36°,
∵BD=CD,AB=AC,
∴AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣36°=54°.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC,
∵EF∥BC,
∴∠FEB=∠CBE,
∴∠FBE=∠FEB,
∴FB=FE.
【点评】本题考查等腰三角形的性质,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
●(3分)(\l "原题2018包头0826" 2018·包头8/26)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
【考点】等腰直角三角形.有
【分析】由AB=AC知∠B=∠C,据此得2∠C+∠BAC=180°,结合∠C+∠BAC=145°可知∠C=35°,根据∠DAE=90°、AD=AE知∠AED=45°,利用∠EDC=∠AED﹣∠C可得答案.
【解答】解:∵AB=AC,
∴∠B=∠C,
∴∠B+∠C+∠BAC=2∠C+∠BAC=180°,
又∵∠C+∠BAC=145°,
∴∠C=35°,
∵∠DAE=90°,AD=AE,
∴∠AED=45°,
∴∠EDC=∠AED﹣∠C=10°,
故选:D.
【点评】本题主要考查等腰直角三角形,解题的关键是掌握等腰直角三角形和等腰三角形的性质及三角形的内角和定理、外角的性质.
●(3分)(\l "原题2016北京1429" 2016?北京14/29) 如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m, 已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为 m.
答案:3
考点:等腰直角三角形判定与性质.
解析:方法一:
如下图,因为小军、小珠都身高与影长相等,所以,
∠E=∠F=45°,所以,AB=BE=BF,设路灯的高AB为 x m,
则BD=x-1.5,BC=x-1.8,
又CD=2.7,所以,x-1.5+x-1.8=2.7,解得:x=3(m).
方法二:
如图:
∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,,
即:,,
解得:AB=3 m,
答:路灯的高为3 m.
【分析】根据CD∥AB∥MN,得到△ABE∽△CDE,△ABF∽△MNF,根据相似三角形的性质得到,,即可得到结论.本题考查了中心投影,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.
●(3分)(\l "原题2015黄石0825" 2015?黄石8/25)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B.54° C.18° D.64°
【考点】等腰三角形的性质.
【分析】根据等腰三角形的性质由已知可求得∠A的度数,再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数.
【解答】解:∵AB=AC,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴∠A=36°,
∵BD⊥AC,
∴∠ABD=90°﹣36°=54°.
故选:B.
【点评】本题主要考查等腰三角形的性质,解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题,此题难度一般.
●(3分)(\l "原题2015盐城0728" 2015?盐城7/28)若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A. 12 B. 9 C. 12或9 D. 9或7
考点: 等腰三角形的性质;三角形三边关系.
分析: 利用等腰三角形的性质以及三角形三边关系得出其周长即可.
解答:解:∵一个等腰三角形的两边长分别是2和5,
∴当腰长为2,则2+2<5,此时不成立,
当腰长为5时,则它的周长为:5+5+2=12.
故选:A.
点评: 此题主要考查了等腰三角形的性质以及三角形三边关系,正确分类讨论得出是解题关键.
●(3分)(\l "原题2015鄂尔多斯0924" 2015?鄂尔多斯9/24)下列说法中,正确的有( )
①等腰三角形两边长为2和5,则它的周长是9或12
②无理数 在-2和1之间
③六边形的内角和是外角和的2倍
④若a>b,则a-b>0.它的逆命题是假命题
⑤北偏东30°与南偏东50°的两条射线组成的角为80°
A.1个 B.2个 C.3个 D.4个
【考点】命题与定理
【分析】①利用等腰三角形的性质以及三角形三边关系得出其周长即可.
②利用“夹逼法”计算.
③六边形的内角和是外角和的2倍.
④根据不等式的性质进行判断.
⑤根据方位角的概念和平角的定义解答.
【解答】解:①一个等腰三角形的两边长分别是2和5,
当腰长为2,则,此时不成立,
当腰长为5时,则它的周长为:.
即该三角形的周长是12.
故①错误;
②无理数在和之间.故②正确;
③,即六边形的内角和是外角和的2倍.故③正确;
④若,则.它的逆命题是真命题,故④错误;
⑤北偏东与南偏东的两条射线组成的角为.故⑤错误.
故选:B.
【点评】本题考查了命题.需要掌握不等式的性质,命题与逆命题,等腰三角形的性质以及无理数的大小比较,属于基础题.
●(3分)(\l "原题2015鄂尔多斯1624" 2015?鄂尔多斯16/24)如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG, 垂足为G,MG与BC相交于点H,若MH =8 cm,则BG = cm.
【考点】全等三角形的判定与性质;等腰直角三角形
【分析】如图,作于,延长交的延长线于,构建等腰△、全等三角形△和△,利用等腰三角形的性质和全等三角形的对应边相等得到:,所以.
【解答】解:如图,作于,延长交的延长线于,
∵△中,,,
,
,
,
,
,
,
.
∵MD∥AC,
,
∴△为等腰直角三角形
,
而,
平分,
而,
,即,
,
,
,,
,
在△和△中,
,
∴△≌△(AAS),
,
.
故答案是:4.
【点评】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.
●(3分)(\l "原题2015陕西0626" 2015?陕西6/26)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
【考点】等腰三角形的判定与性质.
【分析】根据已知条件分别求出图中三角形的内角度数,再根据等腰三角形的判定即可找出图中的等腰三角形.
【解答】解:∵AB=AC,
∴△ABC是等腰三角形;
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC=∠ABC=36°,
∴∠A=∠ABD=36°,
∴BD=AD,
∴△ABD是等腰三角形;
在△BCD中,∵∠BDC=180°﹣∠DBC﹣∠C=180°﹣36°﹣72°=72°,
∴∠C=∠BDC=72°,
∴BD=BC,
∴△BCD是等腰三角形;
∵BE=BC,
∴BD=BE,
∴△BDE是等腰三角形;
∴∠BED=(180°﹣36°)÷2=72°,
∴∠ADE=∠BED﹣∠A=72°﹣36°=36°,
∴∠A=∠ADE,
∴DE=AE,
∴△ADE是等腰三角形;
∴图中的等腰三角形有5个.
故选D.
【点评】此题考查了等腰三角形的判定,用到的知识点是等腰三角形的判定、三角形内角和定理、三角形外角的性质、三角形的角平分线定义等,解题时要找出所有的等腰三角形,不要遗漏.
●(3分)(\l "原题2014扬州1028" 2014?扬州10/28)若等腰三角形的两条边长分别为7 cm和14 cm,则它的周长为 cm.
【解答】解:①14cm为腰,7cm为底,此时周长为14+14+7=35cm;
②14cm为底,7cm为腰,则两边和等于第三边无法构成三角形,故舍去.
故其周长是35cm.
故答案为:35.
18
