人教版数学八年级上册第十一章 三角形 习题课 角度计算的专项训练(word版,无答案)
文档属性
| 名称 | 人教版数学八年级上册第十一章 三角形 习题课 角度计算的专项训练(word版,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 99.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 22:30:02 | ||
图片预览

文档简介
1164590010756900习题课 角度计算的专项训练
01 课堂精讲精练
类型1 直接利用三角形的内、外角性质求角度
【例1】 (佛山顺德区期末)如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2= .
【变式1】 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于 .
类型2 借助三角形的角平分线、高的性质求角度
【例2】 如图,在△ABC中,∠ABC=50°,∠ACB=70°,AD平分∠BAC.过点D作DE⊥AB于点E,则∠ADE的度数是 .
【变式2】 如图,在△ABC中,∠B=60°,AD是△ABC的外角的平分线,DE⊥AC,则∠γ= .
37052252286025050751181101095375100965-3810062865
例1 变式1 例2 变式2
类型3 借助平行线的性质求角度
【例3】 (葫芦岛中考)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=165°,则∠B的度数为 .
【变式3】 (重庆中考)如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,则∠BDC的度数为 .
类型4 借助学具的特征求角度
【例4】 (泰安中考)如图,将一张含有30°角的三角形纸片的两个顶点叠放在长方形的两条对边上.若∠2=44°,则∠1的大小为 .
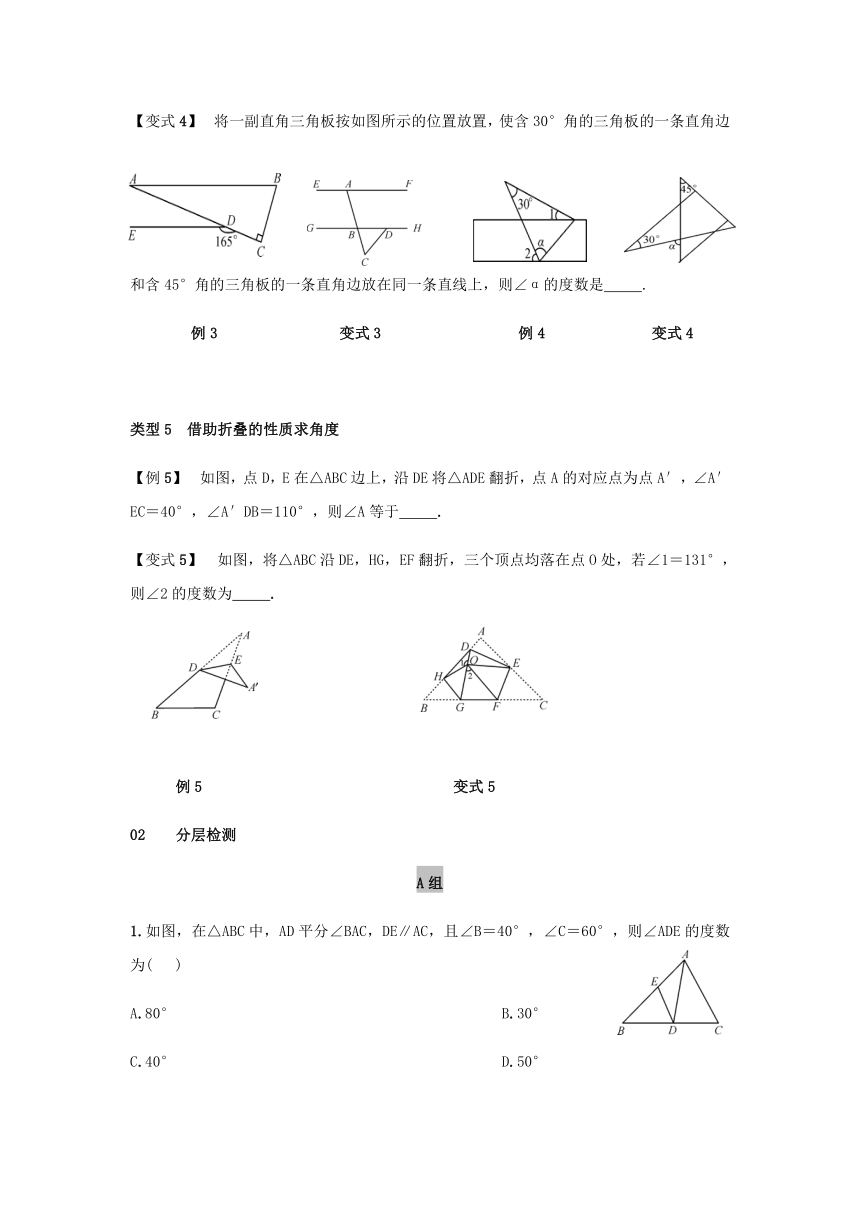
434340064960530194256858001562100676275-9525613410【变式4】 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是 .
例3 变式3 例4 变式4
类型5 借助折叠的性质求角度
【例5】 如图,点D,E在△ABC边上,沿DE将△ADE翻折,点A的对应点为点A′,∠A′EC=40°,∠A′DB=110°,则∠A等于 .
【变式5】 如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为 .
19050057150255587524765
例5 变式5
02 分层检测
42849803219451.如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠B=40°,∠C=60°,则∠ADE的度数为( )
A.80° B.30°
C.40° D.50°
4504055476252.将一副三角板按如图位置摆放,若∠BDE=75°,则∠AMD的度数是( )
A.75° B.80°
C.85° D.90°
43707054552953.如图所示,将三角形ABC沿AB方向平移后,到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠1的度数为( )
A.30° B.40°
C.50° D.60°
4.如图,已知四边形纸片ABCD,其中∠B=120°,∠D=54°,现将其右下角向内折出△PC′R,恰使C′P∥AB,RC′∥AD,则∠C的度数是 .
5.如图,将三角尺ABC和三角尺DFF(其中∠A=∠E=90°,∠C=60°,∠F=45°)摆放在一起,使得点A,D,B,E在同一条直线上,BC交DF于点M,那么∠CMF度数等于 .
260413515811586550532385
3718560244475第5题
第5题
175641042545第4题
第4题
4561205230505
6.如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A.110° B.120°
C.130° D.140°
41706804419607.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC相交于点F.
(1)填空:∠AFC= ;
(2)求∠EDF的度数.
8.如图,在△ABC中,AD平分∠BAC,EG⊥AD,且分别交AB,AD,AC及BC的延长线于点E,H,F,G.若∠B=45°,∠ACB=75°,则∠G的度数为 .
9.已知,如图,AD是BC边上的高,AE平分∠BAC,试探究∠DAE与∠B,∠C之间的数量关系.
01 课堂精讲精练
类型1 直接利用三角形的内、外角性质求角度
【例1】 (佛山顺德区期末)如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2= .
【变式1】 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于 .
类型2 借助三角形的角平分线、高的性质求角度
【例2】 如图,在△ABC中,∠ABC=50°,∠ACB=70°,AD平分∠BAC.过点D作DE⊥AB于点E,则∠ADE的度数是 .
【变式2】 如图,在△ABC中,∠B=60°,AD是△ABC的外角的平分线,DE⊥AC,则∠γ= .
37052252286025050751181101095375100965-3810062865
例1 变式1 例2 变式2
类型3 借助平行线的性质求角度
【例3】 (葫芦岛中考)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=165°,则∠B的度数为 .
【变式3】 (重庆中考)如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,则∠BDC的度数为 .
类型4 借助学具的特征求角度
【例4】 (泰安中考)如图,将一张含有30°角的三角形纸片的两个顶点叠放在长方形的两条对边上.若∠2=44°,则∠1的大小为 .
434340064960530194256858001562100676275-9525613410【变式4】 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是 .
例3 变式3 例4 变式4
类型5 借助折叠的性质求角度
【例5】 如图,点D,E在△ABC边上,沿DE将△ADE翻折,点A的对应点为点A′,∠A′EC=40°,∠A′DB=110°,则∠A等于 .
【变式5】 如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为 .
19050057150255587524765
例5 变式5
02 分层检测
42849803219451.如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠B=40°,∠C=60°,则∠ADE的度数为( )
A.80° B.30°
C.40° D.50°
4504055476252.将一副三角板按如图位置摆放,若∠BDE=75°,则∠AMD的度数是( )
A.75° B.80°
C.85° D.90°
43707054552953.如图所示,将三角形ABC沿AB方向平移后,到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠1的度数为( )
A.30° B.40°
C.50° D.60°
4.如图,已知四边形纸片ABCD,其中∠B=120°,∠D=54°,现将其右下角向内折出△PC′R,恰使C′P∥AB,RC′∥AD,则∠C的度数是 .
5.如图,将三角尺ABC和三角尺DFF(其中∠A=∠E=90°,∠C=60°,∠F=45°)摆放在一起,使得点A,D,B,E在同一条直线上,BC交DF于点M,那么∠CMF度数等于 .
260413515811586550532385
3718560244475第5题
第5题
175641042545第4题
第4题
4561205230505
6.如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A.110° B.120°
C.130° D.140°
41706804419607.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC相交于点F.
(1)填空:∠AFC= ;
(2)求∠EDF的度数.
8.如图,在△ABC中,AD平分∠BAC,EG⊥AD,且分别交AB,AD,AC及BC的延长线于点E,H,F,G.若∠B=45°,∠ACB=75°,则∠G的度数为 .
9.已知,如图,AD是BC边上的高,AE平分∠BAC,试探究∠DAE与∠B,∠C之间的数量关系.
