人教新版 七年级数学(上)学期 1.3.1有理数的加法同步练习试卷 (word版,含解析)
文档属性
| 名称 | 人教新版 七年级数学(上)学期 1.3.1有理数的加法同步练习试卷 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 06:32:23 | ||
图片预览


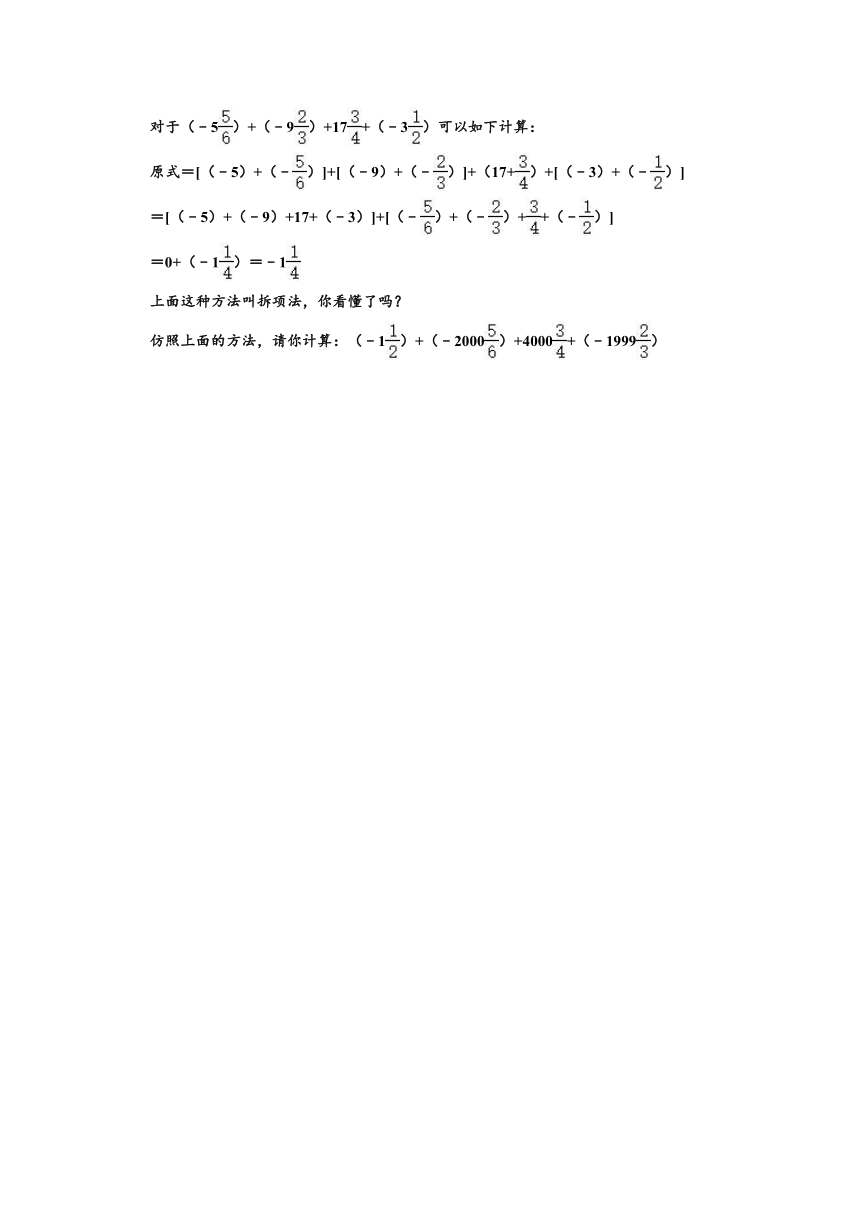

文档简介
1.3.1 有理数的加法 同步练习卷
一、选择题(共10小题).
1.(3分)计算:(﹣3)+4的结果是( )
A.﹣7 B.﹣1 C.1 D.7
2.(3分)若a与1互为相反数,则|a+1|等于( )
A.﹣1 B.0 C.1 D.2
3.(3分)一只蜗牛从深度为10米的井底向上爬3米,然后向下爬1米,接着又向上爬3米,然后又向下爬1米,则此时蜗牛离井口的距离为( )
A.4米 B.5米 C.6米 D.7米
4.(3分)如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>﹣b>﹣a B.a>﹣a>b>﹣b C.b>a>﹣b>﹣a D.﹣a>b>﹣b>a
5.(3分)如果两个数的和是负数,那么这两个数( )
A.同是正数 B.同为负数
C.至少有一个为正数 D.至少有一个为负数
6.(3分)佳佳家冰箱冷冻室的温度为﹣15℃,求调高3℃后的温度,这个过程可以用下列算式表示的是( )
A.﹣15+(﹣3)=﹣18 B.15+(﹣3)=12
C.﹣15+3=﹣12 D.15+(+3)=18
7.(3分)若两个非零有理数a,b,满足|a|=a,|b|=﹣b,a+b<0,则a,b的取值符合题意的是( )
A.a=2,b=﹣1 B.a=﹣2,b=1 C.a=1,b=﹣2 D.a=﹣1,b=﹣2
8.(3分)一个数是9,另一个数比9的相反数大2,那么这两个数的和为( )
A.2 B.﹣2 C.20 D.﹣20
9.(3分)计算1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是( )
A.﹣1005 B.﹣2010 C.0 D.﹣1
10.(3分)计算(+)+(﹣3.5)+(﹣6)+(+2.5)+(+6)+(+)的结果是( )
A.12 B.﹣12 C. D.0
二、填空题
11.(3分)已知|a|=3,|b|=6,a>b,则a+b= .
12.(3分)绝对值小于2016的整数有 个,它们的和是 .
13.(3分)x是绝对值最小的有理数,y是最小的正整数,z是最大的负整数,则x+y+z= .
14.(3分)在横线上填上适当的数.
(1) +4=﹣6;
(2)(﹣5)+ =﹣11.
15.(3分)已知x是整数,并且﹣3<x<2,则x可能取的所有数值的和是 .
16.(3分)北京与巴黎的时差为﹣7时(负数表示同一时刻比北京晚的时数),如果巴黎时间为1月24日8时,则北京的时间是 .
三、解答题
17.已知|a|=8,|b|=2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
18.用简便方法计算:
某产粮专业户出售余粮10袋,每袋重量如下(单位:千克):199、201、197、203、200、195、197、199、202、196.
(1)如果每袋余粮以200千克为标准,求这10袋余粮总计超过多少千克或者不足多少千克?
(2)这10袋余粮一共多少千克?
19.计算:
(1)(﹣1.25)+(﹣5);
(2)﹣+;
(3)﹣15+(+3)+15;
(4)﹣10+12.
20.列式,并计算:
(1)﹣105的绝对值加上12的相反数的和是多少?
(2)﹣15的相反数,加上﹣27的和是多少?
21.阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)=﹣1
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1)+(﹣2000)+4000+(﹣1999)
参考答案
一、选择题
1.(3分)计算:(﹣3)+4的结果是( )
A.﹣7 B.﹣1 C.1 D.7
解:原式=+(4﹣3)=1.
故选:C.
2.(3分)若a与1互为相反数,则|a+1|等于( )
A.﹣1 B.0 C.1 D.2
解:因为互为相反数的两数和为0,所以a+1=0;
因为0的绝对值是0,则|a+1|=|0|=0.
故选:B.
3.(3分)一只蜗牛从深度为10米的井底向上爬3米,然后向下爬1米,接着又向上爬3米,然后又向下爬1米,则此时蜗牛离井口的距离为( )
A.4米 B.5米 C.6米 D.7米
解:向上爬记作“+”,往下爬记作“﹣”
蜗牛离井口的距离为10﹣3﹣(﹣1)﹣3﹣(﹣1)=10﹣3+1﹣3+1=6(米)
故选:C.
4.(3分)如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>﹣b>﹣a B.a>﹣a>b>﹣b C.b>a>﹣b>﹣a D.﹣a>b>﹣b>a
解:∵a<0,b>0
∴﹣a>0﹣b<0
∵a+b<0
∴负数a的绝对值较大
∴﹣a>b>﹣b>a.
故选:D.
5.(3分)如果两个数的和是负数,那么这两个数( )
A.同是正数 B.同为负数
C.至少有一个为正数 D.至少有一个为负数
解:两个数的和是负数,
这两个数至少有一个为负数.
故选:D.
6.(3分)佳佳家冰箱冷冻室的温度为﹣15℃,求调高3℃后的温度,这个过程可以用下列算式表示的是( )
A.﹣15+(﹣3)=﹣18 B.15+(﹣3)=12
C.﹣15+3=﹣12 D.15+(+3)=18
解:佳佳家冰箱冷冻室的温度为﹣15℃,求调高3℃后的温度,这个过程可以用下列算式表示的是﹣15+3=﹣12.
故选:C.
7.(3分)若两个非零有理数a,b,满足|a|=a,|b|=﹣b,a+b<0,则a,b的取值符合题意的是( )
A.a=2,b=﹣1 B.a=﹣2,b=1 C.a=1,b=﹣2 D.a=﹣1,b=﹣2
解:∵|a|=a,|b|=﹣b,a+b<0,
∴a>0,b<0,且|a|<|b|,
在四个选项中只有C选项符合,
故选:C.
8.(3分)一个数是9,另一个数比9的相反数大2,那么这两个数的和为( )
A.2 B.﹣2 C.20 D.﹣20
解:设一个数为a,另一个数为b,由题意得a=9,b=﹣9+2=﹣7,则a+b=9+(﹣7)=2.故选A.
9.(3分)计算1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是( )
A.﹣1005 B.﹣2010 C.0 D.﹣1
解:这从1到2010一共2010个数,相邻两个数之差都为﹣1,
所以1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是﹣1005.
故选:A.
10.(3分)计算(+)+(﹣3.5)+(﹣6)+(+2.5)+(+6)+(+)的结果是( )
A.12 B.﹣12 C. D.0
解:原式=(+)+(﹣3.5+2.5)+(﹣6+6)=1﹣1+0=0,
故选:D.
二、填空题
11.(3分)已知|a|=3,|b|=6,a>b,则a+b= ﹣9或﹣3 .
解:∵|a|=3,|b|=6,且a>b,
∴a=±3,b=﹣6,
当a=﹣3,b=﹣6时,a+b=﹣3﹣6=﹣9;
当a=3,b=﹣6时,a+b=3﹣6=﹣3.
故答案为:﹣9或﹣3.
12.(3分)绝对值小于2016的整数有 4031 个,它们的和是 0 .
解:绝对值小于2016的整数有﹣2015、﹣2014…、﹣1、0、1…2014、2015共4031个,
它们的和为(﹣2015+2015)+(﹣2014+2014)+…+(﹣1+1)+0=0,
故答案为:4031;0.
13.(3分)x是绝对值最小的有理数,y是最小的正整数,z是最大的负整数,则x+y+z= 0 .
解:∵x是绝对值最小的有理数,y是最小的正整数,z是最大的负整数,
∴x=0,y=1,z=﹣1,
则x+y+z=0+1﹣1=0.
故答案为:0.
14.(3分)在横线上填上适当的数.
(1) ﹣10 +4=﹣6;
(2)(﹣5)+ (﹣6) =﹣11.
解:(1)﹣10+4=﹣6;
(2)(﹣5)+(﹣6)=﹣11.
故答案为:﹣10;(﹣6).
15.(3分)已知x是整数,并且﹣3<x<2,则x可能取的所有数值的和是 ﹣2 .
解:∵x是整数,并且﹣3<x<2,
∴x=﹣2,﹣1,0,1,
之和为﹣2﹣1+0+1=﹣2,
故答案为:﹣2
16.(3分)北京与巴黎的时差为﹣7时(负数表示同一时刻比北京晚的时数),如果巴黎时间为1月24日8时,则北京的时间是 1月24日15时 .
解:由题意得8+7=15(时),
答:北京的时间是1月24日15时.
故答案为:1月24日15时.
三、解答题
17.已知|a|=8,|b|=2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
解:(1)∵|a|=8,|b|=2,且a,b同号,
∴a=8,b=2;a=﹣8,b=﹣2,
则a+b=10或﹣10;
(2)∵|a|=8,|b|=2,且a,b异号,
∴a=8,b=﹣2;a=﹣8,b=2,
则a+b=6或﹣6.
18.用简便方法计算:
某产粮专业户出售余粮10袋,每袋重量如下(单位:千克):199、201、197、203、200、195、197、199、202、196.
(1)如果每袋余粮以200千克为标准,求这10袋余粮总计超过多少千克或者不足多少千克?
(2)这10袋余粮一共多少千克?
解:(1)以200千克为基准,超过200千克的数记作正数,不足200千克的数记作负数,则这10袋余粮对应的数分别为:﹣1、+1、﹣3、+3、0、﹣5、﹣3、﹣1、+2、﹣4.
(﹣1)+(+1)+(﹣3)+(+3)+0+(﹣5)+(﹣3)+(﹣1)+(+2)+(﹣4)=﹣11.
答:这10袋余粮总计不足11千克.
(2)200×10+(﹣11)=2000﹣11=1989.
答:这10袋余粮一共1989千克.
19.计算:
(1)(﹣1.25)+(﹣5);
(2)﹣+;
(3)﹣15+(+3)+15;
(4)﹣10+12.
解:(1)原式=﹣7
(2)原式=
(3)原式=3
(4)原式=2
20.列式,并计算:
(1)﹣105的绝对值加上12的相反数的和是多少?
(2)﹣15的相反数,加上﹣27的和是多少?
解:(1)|﹣105|+(﹣12)=105+(﹣12)=93;
(2)﹣(﹣15)+(﹣27)=15+(﹣27)=﹣12.
21.阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)=﹣1
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1)+(﹣2000)+4000+(﹣1999)
解:原式=[(﹣1)+(﹣)]+[(﹣2000)+(﹣)]+(4000+)+[(﹣1999)+(﹣)]
=[(﹣1)+(﹣2000)+4000+(﹣1999)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣)
=﹣.
一、选择题(共10小题).
1.(3分)计算:(﹣3)+4的结果是( )
A.﹣7 B.﹣1 C.1 D.7
2.(3分)若a与1互为相反数,则|a+1|等于( )
A.﹣1 B.0 C.1 D.2
3.(3分)一只蜗牛从深度为10米的井底向上爬3米,然后向下爬1米,接着又向上爬3米,然后又向下爬1米,则此时蜗牛离井口的距离为( )
A.4米 B.5米 C.6米 D.7米
4.(3分)如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>﹣b>﹣a B.a>﹣a>b>﹣b C.b>a>﹣b>﹣a D.﹣a>b>﹣b>a
5.(3分)如果两个数的和是负数,那么这两个数( )
A.同是正数 B.同为负数
C.至少有一个为正数 D.至少有一个为负数
6.(3分)佳佳家冰箱冷冻室的温度为﹣15℃,求调高3℃后的温度,这个过程可以用下列算式表示的是( )
A.﹣15+(﹣3)=﹣18 B.15+(﹣3)=12
C.﹣15+3=﹣12 D.15+(+3)=18
7.(3分)若两个非零有理数a,b,满足|a|=a,|b|=﹣b,a+b<0,则a,b的取值符合题意的是( )
A.a=2,b=﹣1 B.a=﹣2,b=1 C.a=1,b=﹣2 D.a=﹣1,b=﹣2
8.(3分)一个数是9,另一个数比9的相反数大2,那么这两个数的和为( )
A.2 B.﹣2 C.20 D.﹣20
9.(3分)计算1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是( )
A.﹣1005 B.﹣2010 C.0 D.﹣1
10.(3分)计算(+)+(﹣3.5)+(﹣6)+(+2.5)+(+6)+(+)的结果是( )
A.12 B.﹣12 C. D.0
二、填空题
11.(3分)已知|a|=3,|b|=6,a>b,则a+b= .
12.(3分)绝对值小于2016的整数有 个,它们的和是 .
13.(3分)x是绝对值最小的有理数,y是最小的正整数,z是最大的负整数,则x+y+z= .
14.(3分)在横线上填上适当的数.
(1) +4=﹣6;
(2)(﹣5)+ =﹣11.
15.(3分)已知x是整数,并且﹣3<x<2,则x可能取的所有数值的和是 .
16.(3分)北京与巴黎的时差为﹣7时(负数表示同一时刻比北京晚的时数),如果巴黎时间为1月24日8时,则北京的时间是 .
三、解答题
17.已知|a|=8,|b|=2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
18.用简便方法计算:
某产粮专业户出售余粮10袋,每袋重量如下(单位:千克):199、201、197、203、200、195、197、199、202、196.
(1)如果每袋余粮以200千克为标准,求这10袋余粮总计超过多少千克或者不足多少千克?
(2)这10袋余粮一共多少千克?
19.计算:
(1)(﹣1.25)+(﹣5);
(2)﹣+;
(3)﹣15+(+3)+15;
(4)﹣10+12.
20.列式,并计算:
(1)﹣105的绝对值加上12的相反数的和是多少?
(2)﹣15的相反数,加上﹣27的和是多少?
21.阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)=﹣1
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1)+(﹣2000)+4000+(﹣1999)
参考答案
一、选择题
1.(3分)计算:(﹣3)+4的结果是( )
A.﹣7 B.﹣1 C.1 D.7
解:原式=+(4﹣3)=1.
故选:C.
2.(3分)若a与1互为相反数,则|a+1|等于( )
A.﹣1 B.0 C.1 D.2
解:因为互为相反数的两数和为0,所以a+1=0;
因为0的绝对值是0,则|a+1|=|0|=0.
故选:B.
3.(3分)一只蜗牛从深度为10米的井底向上爬3米,然后向下爬1米,接着又向上爬3米,然后又向下爬1米,则此时蜗牛离井口的距离为( )
A.4米 B.5米 C.6米 D.7米
解:向上爬记作“+”,往下爬记作“﹣”
蜗牛离井口的距离为10﹣3﹣(﹣1)﹣3﹣(﹣1)=10﹣3+1﹣3+1=6(米)
故选:C.
4.(3分)如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>﹣b>﹣a B.a>﹣a>b>﹣b C.b>a>﹣b>﹣a D.﹣a>b>﹣b>a
解:∵a<0,b>0
∴﹣a>0﹣b<0
∵a+b<0
∴负数a的绝对值较大
∴﹣a>b>﹣b>a.
故选:D.
5.(3分)如果两个数的和是负数,那么这两个数( )
A.同是正数 B.同为负数
C.至少有一个为正数 D.至少有一个为负数
解:两个数的和是负数,
这两个数至少有一个为负数.
故选:D.
6.(3分)佳佳家冰箱冷冻室的温度为﹣15℃,求调高3℃后的温度,这个过程可以用下列算式表示的是( )
A.﹣15+(﹣3)=﹣18 B.15+(﹣3)=12
C.﹣15+3=﹣12 D.15+(+3)=18
解:佳佳家冰箱冷冻室的温度为﹣15℃,求调高3℃后的温度,这个过程可以用下列算式表示的是﹣15+3=﹣12.
故选:C.
7.(3分)若两个非零有理数a,b,满足|a|=a,|b|=﹣b,a+b<0,则a,b的取值符合题意的是( )
A.a=2,b=﹣1 B.a=﹣2,b=1 C.a=1,b=﹣2 D.a=﹣1,b=﹣2
解:∵|a|=a,|b|=﹣b,a+b<0,
∴a>0,b<0,且|a|<|b|,
在四个选项中只有C选项符合,
故选:C.
8.(3分)一个数是9,另一个数比9的相反数大2,那么这两个数的和为( )
A.2 B.﹣2 C.20 D.﹣20
解:设一个数为a,另一个数为b,由题意得a=9,b=﹣9+2=﹣7,则a+b=9+(﹣7)=2.故选A.
9.(3分)计算1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是( )
A.﹣1005 B.﹣2010 C.0 D.﹣1
解:这从1到2010一共2010个数,相邻两个数之差都为﹣1,
所以1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是﹣1005.
故选:A.
10.(3分)计算(+)+(﹣3.5)+(﹣6)+(+2.5)+(+6)+(+)的结果是( )
A.12 B.﹣12 C. D.0
解:原式=(+)+(﹣3.5+2.5)+(﹣6+6)=1﹣1+0=0,
故选:D.
二、填空题
11.(3分)已知|a|=3,|b|=6,a>b,则a+b= ﹣9或﹣3 .
解:∵|a|=3,|b|=6,且a>b,
∴a=±3,b=﹣6,
当a=﹣3,b=﹣6时,a+b=﹣3﹣6=﹣9;
当a=3,b=﹣6时,a+b=3﹣6=﹣3.
故答案为:﹣9或﹣3.
12.(3分)绝对值小于2016的整数有 4031 个,它们的和是 0 .
解:绝对值小于2016的整数有﹣2015、﹣2014…、﹣1、0、1…2014、2015共4031个,
它们的和为(﹣2015+2015)+(﹣2014+2014)+…+(﹣1+1)+0=0,
故答案为:4031;0.
13.(3分)x是绝对值最小的有理数,y是最小的正整数,z是最大的负整数,则x+y+z= 0 .
解:∵x是绝对值最小的有理数,y是最小的正整数,z是最大的负整数,
∴x=0,y=1,z=﹣1,
则x+y+z=0+1﹣1=0.
故答案为:0.
14.(3分)在横线上填上适当的数.
(1) ﹣10 +4=﹣6;
(2)(﹣5)+ (﹣6) =﹣11.
解:(1)﹣10+4=﹣6;
(2)(﹣5)+(﹣6)=﹣11.
故答案为:﹣10;(﹣6).
15.(3分)已知x是整数,并且﹣3<x<2,则x可能取的所有数值的和是 ﹣2 .
解:∵x是整数,并且﹣3<x<2,
∴x=﹣2,﹣1,0,1,
之和为﹣2﹣1+0+1=﹣2,
故答案为:﹣2
16.(3分)北京与巴黎的时差为﹣7时(负数表示同一时刻比北京晚的时数),如果巴黎时间为1月24日8时,则北京的时间是 1月24日15时 .
解:由题意得8+7=15(时),
答:北京的时间是1月24日15时.
故答案为:1月24日15时.
三、解答题
17.已知|a|=8,|b|=2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
解:(1)∵|a|=8,|b|=2,且a,b同号,
∴a=8,b=2;a=﹣8,b=﹣2,
则a+b=10或﹣10;
(2)∵|a|=8,|b|=2,且a,b异号,
∴a=8,b=﹣2;a=﹣8,b=2,
则a+b=6或﹣6.
18.用简便方法计算:
某产粮专业户出售余粮10袋,每袋重量如下(单位:千克):199、201、197、203、200、195、197、199、202、196.
(1)如果每袋余粮以200千克为标准,求这10袋余粮总计超过多少千克或者不足多少千克?
(2)这10袋余粮一共多少千克?
解:(1)以200千克为基准,超过200千克的数记作正数,不足200千克的数记作负数,则这10袋余粮对应的数分别为:﹣1、+1、﹣3、+3、0、﹣5、﹣3、﹣1、+2、﹣4.
(﹣1)+(+1)+(﹣3)+(+3)+0+(﹣5)+(﹣3)+(﹣1)+(+2)+(﹣4)=﹣11.
答:这10袋余粮总计不足11千克.
(2)200×10+(﹣11)=2000﹣11=1989.
答:这10袋余粮一共1989千克.
19.计算:
(1)(﹣1.25)+(﹣5);
(2)﹣+;
(3)﹣15+(+3)+15;
(4)﹣10+12.
解:(1)原式=﹣7
(2)原式=
(3)原式=3
(4)原式=2
20.列式,并计算:
(1)﹣105的绝对值加上12的相反数的和是多少?
(2)﹣15的相反数,加上﹣27的和是多少?
解:(1)|﹣105|+(﹣12)=105+(﹣12)=93;
(2)﹣(﹣15)+(﹣27)=15+(﹣27)=﹣12.
21.阅读下面文字:
对于(﹣5)+(﹣9)+17+(﹣3)可以如下计算:
原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]
=[(﹣5)+(﹣9)+17+(﹣3)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣1)=﹣1
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1)+(﹣2000)+4000+(﹣1999)
解:原式=[(﹣1)+(﹣)]+[(﹣2000)+(﹣)]+(4000+)+[(﹣1999)+(﹣)]
=[(﹣1)+(﹣2000)+4000+(﹣1999)]+[(﹣)+(﹣)++(﹣)]
=0+(﹣)
=﹣.
