人教版高中物理选修3—1第1章第9节带电粒子在电场中的运动
文档属性
| 名称 | 人教版高中物理选修3—1第1章第9节带电粒子在电场中的运动 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-27 12:42:12 | ||
图片预览









文档简介
【学习目标】
1、掌握带电粒子在电场中的运动规律
2、分析解决加速和偏转问题
【学习重点】
1、带电粒子在电场中的运动规律
【学习难点】
1、运用电学知识和力学知识综合处理偏转问题
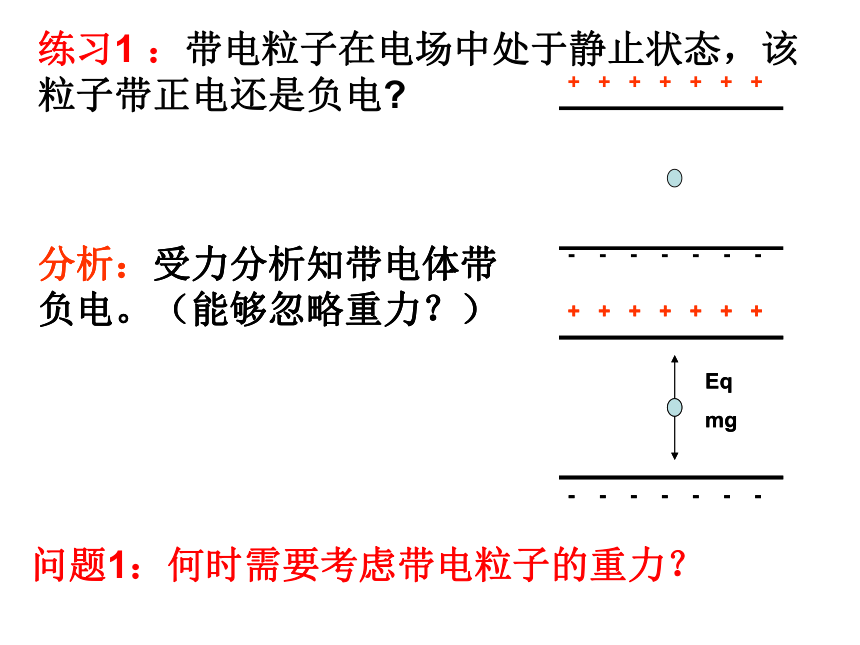
练习1 :带电粒子在电场中处于静止状态,该粒子带正电还是负电?
+ + + + + + +
- - - - - - -
练习1 :带电粒子在电场中处于静止状态,该粒子带正电还是负电?
+ + + + + + +
- - - - - - -
Eq
mg
分析:受力分析知带电体带负电。(能够忽略重力?)
+ + + + + + +
- - - - - - -
问题1:何时需要考虑带电粒子的重力?
+ + + + + + +
- - - - - - -
Eq
mg
分析:受力分析知带电体带负电。(能够忽略重力?)
一、带电粒子的重力是否忽略
1、基本粒子:如电子、质子、离子、α 粒子等在没
有明确指出或暗示下重力一般忽略不计。
2、带电颗粒:如油滴、液滴、尘埃、带电小球在没有明
确指出或暗示下重力一般不能忽略。
一.带电粒子的加速
【问题情境一】两块平行正对的金属板A、B,相距为d,带有等量异种电荷,电压为U。如图所示,一质量为m,电荷量为e的质子从A板处由静止开始运动,用几种方法可求其到达B板时的速度v?
A
B
a =
F
m
eU
md
=
v2=2ad
可求出v=
√
2eU
m
可求出v=
√
2eU
m
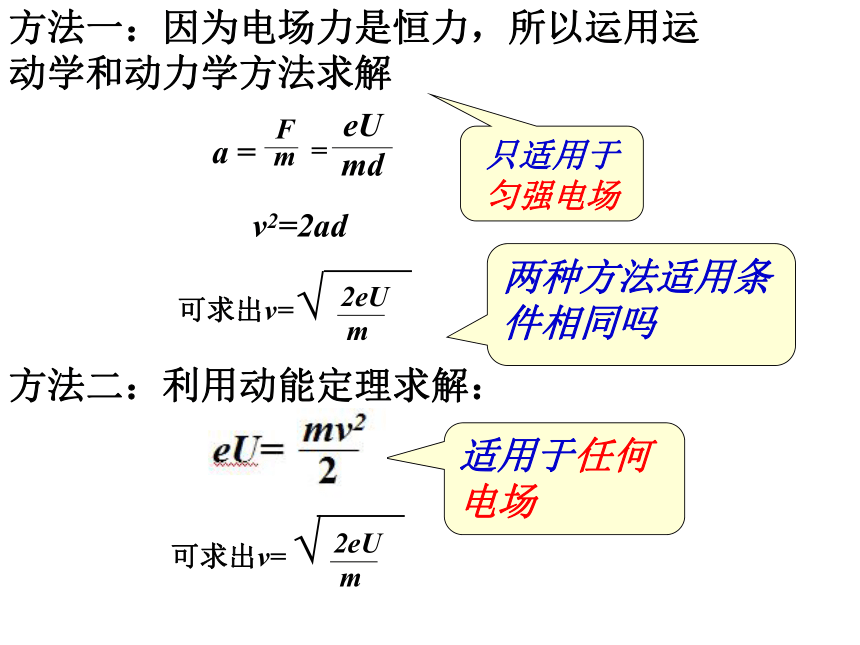
只适用于匀强电场
适用于任何电场
方法一:因为电场力是恒力,所以运用运动学和动力学方法求解
方法二:利用动能定理求解:
两种方法适用条件相同吗
1. 非匀强电场中,如何计算?
例题1:如图所示,在点电荷+Q的电场中有A、B两点,当质子和α粒子分别从A点由静止释放到达B点时,它们的速度大小之比为多少?(质子带电荷量有+e,质量为m,α粒子带电荷量为+2e,质量为4m)
1. 非匀强电场中,如何计算?
电场力做功,只于始末位置电势差有关
用动能定理
v0
q
m
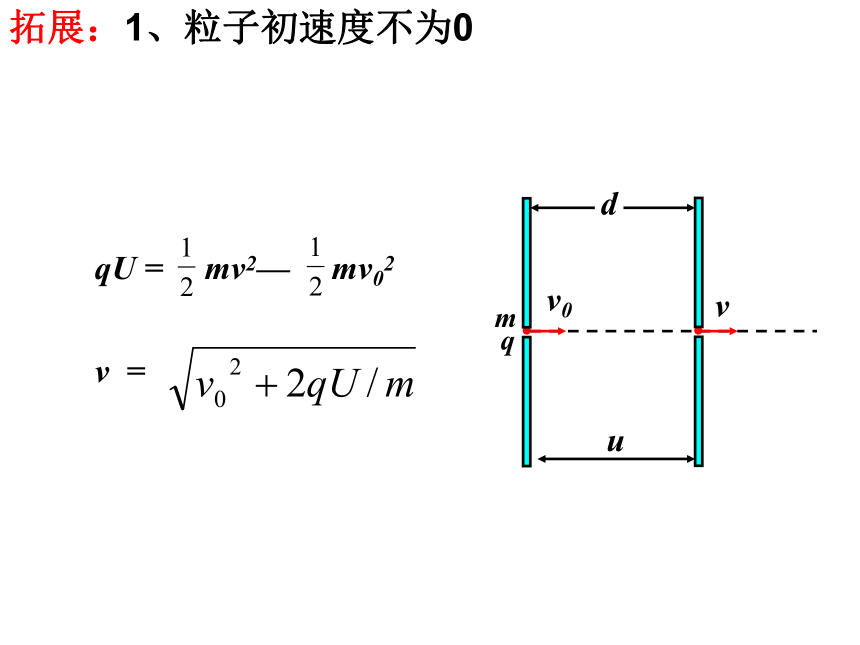
qU = mv2— mv02
v =
v
u
d
拓展:1、粒子初速度不为0
nqU = mv2— mv02
v =
v
u
d
拓展:2、粒子初速度不为0,经过多个电场加速
v0
q
m
u
d
u
d
直线加速器
应用:
北京正负电子对撞机的直线加速器
应用:
2. 若粒子以初速度v0沿垂直场强方向进入电
场,粒子的运动情况如何?
观察实验
【问题情境二】如图所示,真空中两极板水平放置,间距为d,电势差为U,板长为l。质量为m带电荷量为q的粒子以垂直于电场方向的速度v0从两板中间进入匀强电场。(不计粒子的重力)
相互交流讨论一下, 能不能解决的问题?
二、带电粒子在匀强电场中的偏转
3、将粒子的运动如何处理?
1、沿初速度方向做什么运动?
2、沿电场线方向做什么运动?加速度a?
5、出粒子的偏转位移y
4、粒子沿y轴方向的速度vy
6、速度与初速度夹角的tan
二、带电粒子在匀强电场中的偏转
l
d
+
- - - - - - - - - - -
+ + + + + + + + + + +
U
v0
q、m
F
+
v
v0
vy
y
θ
偏转角
侧移
类平抛运动
例题2:如图所示,一个电子以4.0×106m/s的速度沿与电场垂直的方向从A点飞进匀强电场,并且从另一端B点沿与场强方向成1500角方向飞出,那么,A、B两点间的电势差为多少伏?(电子的质量为9.1×10-31 kg )
·
vA
A
B
·
1500
vB
vA
vy
600
解:电子垂直进入匀强电场中,做类平抛运动
可得 VA=VBcos60°
根据动能定理得
①
②
联立①②两式解出AB两点的电势差
负号说明A点的电势比B点低
+
+
+
-
-
-
例题3:如图,有一电子(电量为e)经电压U0加速后进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场.求: (1)金属板AB的长度 (2)电子穿出电场时的动能 。?
U0
d
A
B
- - - - -
+ + + + +
例题3:如图,有一电子(电量为e)经电压U0加速后进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场.求: (1)金属板AB的长度 (2)电子穿出电场时的动能 。?
U0
d
A
B
- - - - -
+ + + + +
①
②
解:⑴电子被加速后进入偏转电场做类平抛运动.
解:
⑵整个过程由动能定理:
③
④
总结:粒子在电场中加速和偏转
L
三、带电粒子在匀强电场中的加速和偏转
+
+
+
+
+
+
-
-
-
-
-
-
φ
v
v0
vy
+
_
U1
U2
v0
-q
m
y
400-018-
例题4:如图,真空中水平放置的两个相同极板Y和Y'长为L,相距d,足够大的竖直屏与两板右侧相距b.在两板间加上可调偏转电压U,一束质量为m、带电量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出.
(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点;
(2)求两板间所加偏转电压U的范围;
(3)求粒子可能到达屏上区域的长度.
400-018-
解析:(1)设粒子在运动过程中的加速度大小为a,离开偏转电场时偏转距离为y,沿电场方向的速度为vy,偏转角为θ,其反向延长线通过O点,O点与板右端的水平距离为x,则有
θ
x
o
y
θ
v
O
v0
U2
-
+
L
d
Y
F
S
O‘
y
θ
v
O
v0
U2
-
+
L
d
y0
F
S
O‘
y
θ
v
O
v0
U2
-
+
L
d
y0
F
S
O‘
课堂小结:
一、利用电场使带电粒子加速
二、利用电场使带电粒子偏转
从动力学和运动学角度分析
从做功和能量的角度分析
类似平抛运动的分析方法
粒子在与电场垂直的方向上做
匀速直线运动
粒子在与电场平行的方向上做
初速度为零的匀加速运动
1、掌握带电粒子在电场中的运动规律
2、分析解决加速和偏转问题
【学习重点】
1、带电粒子在电场中的运动规律
【学习难点】
1、运用电学知识和力学知识综合处理偏转问题
练习1 :带电粒子在电场中处于静止状态,该粒子带正电还是负电?
+ + + + + + +
- - - - - - -
练习1 :带电粒子在电场中处于静止状态,该粒子带正电还是负电?
+ + + + + + +
- - - - - - -
Eq
mg
分析:受力分析知带电体带负电。(能够忽略重力?)
+ + + + + + +
- - - - - - -
问题1:何时需要考虑带电粒子的重力?
+ + + + + + +
- - - - - - -
Eq
mg
分析:受力分析知带电体带负电。(能够忽略重力?)
一、带电粒子的重力是否忽略
1、基本粒子:如电子、质子、离子、α 粒子等在没
有明确指出或暗示下重力一般忽略不计。
2、带电颗粒:如油滴、液滴、尘埃、带电小球在没有明
确指出或暗示下重力一般不能忽略。
一.带电粒子的加速
【问题情境一】两块平行正对的金属板A、B,相距为d,带有等量异种电荷,电压为U。如图所示,一质量为m,电荷量为e的质子从A板处由静止开始运动,用几种方法可求其到达B板时的速度v?
A
B
a =
F
m
eU
md
=
v2=2ad
可求出v=
√
2eU
m
可求出v=
√
2eU
m
只适用于匀强电场
适用于任何电场
方法一:因为电场力是恒力,所以运用运动学和动力学方法求解
方法二:利用动能定理求解:
两种方法适用条件相同吗
1. 非匀强电场中,如何计算?
例题1:如图所示,在点电荷+Q的电场中有A、B两点,当质子和α粒子分别从A点由静止释放到达B点时,它们的速度大小之比为多少?(质子带电荷量有+e,质量为m,α粒子带电荷量为+2e,质量为4m)
1. 非匀强电场中,如何计算?
电场力做功,只于始末位置电势差有关
用动能定理
v0
q
m
qU = mv2— mv02
v =
v
u
d
拓展:1、粒子初速度不为0
nqU = mv2— mv02
v =
v
u
d
拓展:2、粒子初速度不为0,经过多个电场加速
v0
q
m
u
d
u
d
直线加速器
应用:
北京正负电子对撞机的直线加速器
应用:
2. 若粒子以初速度v0沿垂直场强方向进入电
场,粒子的运动情况如何?
观察实验
【问题情境二】如图所示,真空中两极板水平放置,间距为d,电势差为U,板长为l。质量为m带电荷量为q的粒子以垂直于电场方向的速度v0从两板中间进入匀强电场。(不计粒子的重力)
相互交流讨论一下, 能不能解决的问题?
二、带电粒子在匀强电场中的偏转
3、将粒子的运动如何处理?
1、沿初速度方向做什么运动?
2、沿电场线方向做什么运动?加速度a?
5、出粒子的偏转位移y
4、粒子沿y轴方向的速度vy
6、速度与初速度夹角的tan
二、带电粒子在匀强电场中的偏转
l
d
+
- - - - - - - - - - -
+ + + + + + + + + + +
U
v0
q、m
F
+
v
v0
vy
y
θ
偏转角
侧移
类平抛运动
例题2:如图所示,一个电子以4.0×106m/s的速度沿与电场垂直的方向从A点飞进匀强电场,并且从另一端B点沿与场强方向成1500角方向飞出,那么,A、B两点间的电势差为多少伏?(电子的质量为9.1×10-31 kg )
·
vA
A
B
·
1500
vB
vA
vy
600
解:电子垂直进入匀强电场中,做类平抛运动
可得 VA=VBcos60°
根据动能定理得
①
②
联立①②两式解出AB两点的电势差
负号说明A点的电势比B点低
+
+
+
-
-
-
例题3:如图,有一电子(电量为e)经电压U0加速后进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场.求: (1)金属板AB的长度 (2)电子穿出电场时的动能 。?
U0
d
A
B
- - - - -
+ + + + +
例题3:如图,有一电子(电量为e)经电压U0加速后进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场.求: (1)金属板AB的长度 (2)电子穿出电场时的动能 。?
U0
d
A
B
- - - - -
+ + + + +
①
②
解:⑴电子被加速后进入偏转电场做类平抛运动.
解:
⑵整个过程由动能定理:
③
④
总结:粒子在电场中加速和偏转
L
三、带电粒子在匀强电场中的加速和偏转
+
+
+
+
+
+
-
-
-
-
-
-
φ
v
v0
vy
+
_
U1
U2
v0
-q
m
y
400-018-
例题4:如图,真空中水平放置的两个相同极板Y和Y'长为L,相距d,足够大的竖直屏与两板右侧相距b.在两板间加上可调偏转电压U,一束质量为m、带电量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出.
(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点;
(2)求两板间所加偏转电压U的范围;
(3)求粒子可能到达屏上区域的长度.
400-018-
解析:(1)设粒子在运动过程中的加速度大小为a,离开偏转电场时偏转距离为y,沿电场方向的速度为vy,偏转角为θ,其反向延长线通过O点,O点与板右端的水平距离为x,则有
θ
x
o
y
θ
v
O
v0
U2
-
+
L
d
Y
F
S
O‘
y
θ
v
O
v0
U2
-
+
L
d
y0
F
S
O‘
y
θ
v
O
v0
U2
-
+
L
d
y0
F
S
O‘
课堂小结:
一、利用电场使带电粒子加速
二、利用电场使带电粒子偏转
从动力学和运动学角度分析
从做功和能量的角度分析
类似平抛运动的分析方法
粒子在与电场垂直的方向上做
匀速直线运动
粒子在与电场平行的方向上做
初速度为零的匀加速运动
